Пример программы в MathCad

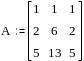
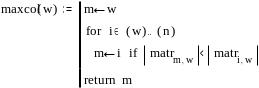
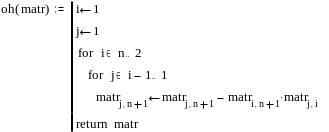
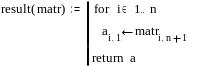
Контрольные вопросы

1. Какой вид имеет матрица коэффициентов после окончания прямого хода в методе Гаусса ?

2. Какие операции выполняются при обратном ходе?

3. Какие преимущества имеет модифицированный метод Гаусса по сравнению с обычным методом?

Лабораторная работа 3 Решение систем линейных алгебраических уравнений методом итераций

Работа выполняется с использованием палитры программирования системы автоматизации математических вычислений Mathcad

Задание на работу:

1. Разработать программу для решения системы линейных алгебраических уравнений методом итераций.

2. В программе предусмотреть проверку существования единственного решения, воспользовавшись процедурой «proverka», рассмотренной в работе № 2.

3. В программе предусмотреть вывод числа итераций, необходимых для достижения заданной точности (точность определяется погрешностью ε)

4. Решить систему уравнений, определенную вариантом задания (задания определены в работе № 2, погрешность ε положить равной 0.0001 ).

5. Найти теоретическую оценку числа итераций, необходимых для достижения заданной точности, и сравнить с фактическим значением.

6. Произвести проверку решения с помощью процедуры решения системы линейных алгебраических уравнений isolve (X:= isolve(A,В)).

7. Изменить матрицу коэффициентов А, сделав систему уравнений линейно зависимой, и проверить работоспособность программы в этом случае.

Требования к оформлению отчета

Отчет должен содержать:

• Название и цель работы

• Задание на работу

• Текст программы на Mathcadе

• Результаты работы программы

• Проверку решения

Контрольные вопросы

1. В каком случае целесообразно применять итерационный метод решения систем линейных алгебраических уравнений ?

2. Сформулируйте условие сходимости итерационного процесса.

3. Что такое l – норма матрицы?

4. Что такое m – норма матрицы?

5. Как оценить количество итераций, необходимое для достижения заданной точности?

Примечание: при выполнении работы используйте вспомогательные материалы, приведенные в работе № 2.

Раздел 3 Решение нелинейных уравнений

Краткое введение. Пусть f(x) = 0 - некоторое уравнение . Число ξ называется корнем или решением данного уравнения , если оно, будучи подставлено в уравнение, обращает его в равенство, т. е. f (ξ) = 0. Число ξ называют также нулем функции y = f(x).

Нахождение действительных корней с определенной точностью можно разбить на два этапа:

1. отделение корней , т. е. установление промежутков, в которых содержится один корень уравнения;

2. вычисление корня, принадлежащего выбранному промежутку, с заданной точностью.

Для отделения корней составляют таблицу значений функции y = f(x) на определенном промежутке изменения аргумента х , и если окажется , что для соседних значений аргументов значения функции имеют разные знаки , то нуль находится между ними.

Возможны и другие способы отделения корней , например графические.

После отделения корней для вычисления корня можно применить следующие методы.

Метод половинного деления

Описание метода.

Пусть дано уравнение

f(x) = 0, (1)

причем функция f(x) непрерывна на отрезке [ a , b] и f(a)f(b) < 0.

Для вычисления корня уравнения (1) , принадлежащего отрезку [ a , b] , найдем середину этого отрезка x₁ = ( a + b ) / 2. Если f( x₁) 0 , то для продолжения вычислений выберем ту из частей банного отрезка [ a, x₁] или [ x_{1 ,} b] , на концах которой функция f(x) имеет противоположные знаки. Концы нового отрезка обозначим через a₁ и b_1.

Новый суженный промежуток [ a₁, b₁ ] снова делим пополам и продолжаем вычисления по разработанной схеме и т. д. В результате получаем либо точный корень уравнения (1) на каком - то этапе , либо последовательность вложенных отрезков [ a , b ] , [ a₁, b₁ ] , . . . , [ a _n, b _n ] , . . таких , что

f(a _n)f(b _n) < 0 ( n = 1 , 2 , . . .) , (2)

b _n - a _n = ( 1/ 2 ⁿ) ( b- a ) (3)

Число ξ - общий предел последовательности { a _n } и { b _n } - является корнем уравнения

f(x) = 0 .

Оценку погрешности решения на n -ом шаге вычислений можно получить из соотношения ( 3 ) в виде

0 < ξ - a _n ( 1/ 2 ⁿ) ( b- a ) = b _n - a _n (4)

Здесь a _n ξ c точностью ε не превышающей ( 1/ 2 ⁿ) ( b- a ).

Y

Y

Y = f ( x )

a₁

X

b

b₁

f

ξ

b₁

a

Рис. 3.1 Наличие единственного корня уравнения на интервале [a,b]

Блок – схема алгоритма, реализующего метод половинного деления, приведена на рис. 3.3.