Блок-схема программы построения кубического сплайна и построения полинома Лагранжа представлены на рис. 4.3 и рис. 4.4

Пусть отрезок [a,b] разбит на n равных частей и в точках x_i (i=0,1,2,...,n; x₀=a, х_n=b) некоторая функция принимает значения y_i. Для переменной x, принадлежащей части разбиения [x_i-1 ,x_i] (i=1,... ,n), определена функция (кубический многочлен)

Здесь - шаг разбиения отрезка.

Неизвестные m_i определяются рекуррентными соотношениями

n₀ = A; m_n = В; m_i = L_im_i+1 + M_i (i=n-1,n-2,...,0)

после предварительного вычисления вспомогательных величин M_i, L_i

по рекуррентным формулам

L₀ = 0, M₀ = m₀, M_i = L_i(M_i-1 – b_i) (i=1,2,...,n-1),

где

Величины А и В должны быть заданы. При построении кубичес­кого сплайна, интерполирующего дифференцируемую функцию y = f (x)

по системе точек, полагают A = f ' (a), S = f ' (b) (краевые условия I типа). Выбор необходимой формулы S_i (x) для заданного значения переменной x определяется целым числом i:

В соот­ветствии c условиями задачи для рассмотренного примера в программах принято m₀ = 1, m_n = 0.

да

i = Цел.часть((х-а)/h) + 1 ; x0 = a + (i -1)h, x1 = x0 + h

m(0) = 1; m(n) = 0; l(0) = 0; h = (b-a)/n

b_i = 3(y_i+1- y_i-1)/h; l_i = -1/(l_i-1 + 4); m_i = l_i(m_i-1 - b_i)

m_i =l_im_i+1 + m_i

нет

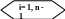
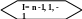
Рис 4.3 Блок-схема программы построения кубического сплайна

Блок – схема программы построения интерполяционного многочлена Лагранжа в комментариях не нуждается.

Рис.4.4 Блок - схема программы построения интерполяционного многочлена Лагранжа

Лабораторная работа 5 Методы интерполирования функций

Работа выполняется с использованием палитры программирования системы автоматизации математических вычислений Mathcad

Задание на работу. В таблице приведены ( в соответствии с вариантами заданий ) значения функций в пяти узлах (с шагом 0.01 ).

1. Найти значения многочлена Лагранжа , интерполирующего функцию f( x ) на заданном отрезке по системе трех равномерно расположенных узлов ( с шагом 0.02 ), в точках (x₀ +x_{2) / 2; (} x₂ + x_{4) /} 2 т. е. в точках x_{1 ,}x ₃ . Полученные результаты сравнить с табличными значениями.

2. Найти значения полинома Ньютона , интерполирующего функцию f( x ) на заданном отрезке по системе трех равномерно расположенных узлов ( с шагом 0.02 ), в точках (x₀ +x_{2) / 2; (} x₂ + x_{4) /} 2 т. е. в точках x_{1 ,}x ₃ . Полученные результаты сравнить с табличными значениями.

3. Построить кубический сплайн отрезке по системе трех равномерно расположенных узлов ( с шагом 0.02 ), в точках (x₀ +x_{2) / 2; (} x₂ + x_{4) /} 2 т. е. в точках x_{1 ,}x ₃

4. Дать оценку точности интерполяции.

Варианты задания

		Номер задания
		1	2	3	4	5	6	7
№	X	e x	e - x	sh x	ch x	sin x	cos x	ln x
1	1.00	2.7183	0.3679	1.1752	1.5431	0.8415	0.5403	0.0000
2	.01	2.7456	0.3642	1.1907	1.5549	0.8468	0.5319	0.0100
3	.02	2.7732	0.3606	1.2063	1.5669	0.8521	0.5234	0.0198
4	.03	2.8011	0.3570	1.2220	1.5790	0.8573	0.5148	0.0296
5	.04	2.8292	0.3535	1.2379	1.5913	0.8624	0.5062	0.0392

		Номер задания
		8	9	10	11	12	13	14
№	X	e x	e - x	sh x	ch x	sin x	cos x	ln x
1	1.05	2.8577	0.3499	1.2539	1.6038	0.8674	0.4976	0.0488
2	.06	2.8864	0.3465	1.2700	1.6164	0.8724	0.4889	0.0583
3	.07	2.9154	0.3430	1.2862	1.6992	0.8772	0.4801	0.0677
4	.08	2.9447	0.3396	1.3025	1.6421	0.8820	0.4713	0.0770
5	.09	2.9743	0.3362	1.3190	1.6552	0.8866	0.4625	0.0862

		Номер задания
		15	16	17	18	19	20	21
№	X	e x	e - x	sh x	ch x	sin x	cos x	ln x
1	1.10	3.0042	0.3329	1.3356	1.6685	0.8912	0.4536	0.0953
2	.11	3.0344	0.3296	1.3524	1.6820	0.8957	0.4447	0.1044
3	.12	3.0649	0.3263	1.3693	1.6956	0.9001	0.4357	0.1133
4	.13	3.0957	0.3230	1.3863	1.7093	0.9044	0.4267	0.1222
5	.14	3.1268	0.3198	1.4035	1.7233	0.9086	0.4176	0.1310

Вспомогательные материалы

1. Пример выполнения работы ( пункт 1 )

Пусть задана функция y = sin x на интервале [ 1.15 , 1.19 ]

X	1.15	1.16	1.17	1.18	1.19
Y	0.9128	0.9168	0.9208	0.9426	0.9284

При задании с шагом 0.2 таблица примет вид:

X	1.15	1.17	1.19
Y	0.9128	0.9208	0.9284

Интерполяционный полином Лагранжа для трех узлов имеет вид

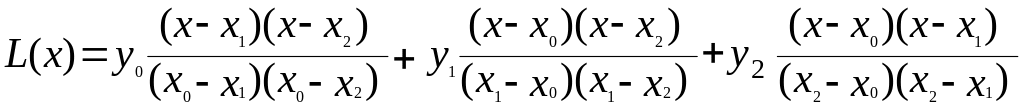
Вычислим по данной формуле значение в точке x = 1.16 . Имеем :

x(0) = 1.15 ; x(1) = 1.17 ; x(2) = 1.19; y(0) =0.9128 ; y(1) = 0.9208; y(2) = 0.9284

Подставляя данные в выражение для L(x), получаем

Полученное значение точно совпадает с табличным для x = 1.16.

Оценим погрешность интерполирования по формуле (2). Имеем n = 2.

f ^{(n + 1)} = -cos (x)

Максимальное значение косинуса не превосходит 1. Следовательно, М _{n +1} равно 1.

= 0.5 * 10 ^{- 6}.

Следовательно, результат интерполирования совпадает с точным значением функции до пяти знаков после запятой.

Разработка программы на Mathcadе трудностей не представляет.

2. Пункт 2 задания выполняется аналогично.

3. Пример Mathcad – программы для построения кубического сплайна приведен ниже.

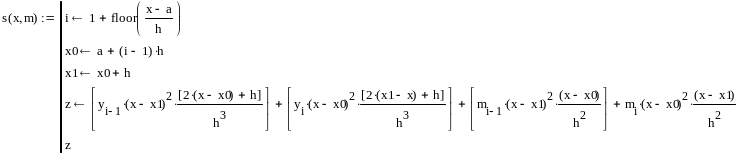
Контрольные вопросы

1.Чему равно значение интерполяционного полинома в узловых точках ?

2. Какова максимальная степень многочлена Лагранжа ?

3. Какова максимальная степень многочлена Ньютона?

4. Как оценивается погрешность интерполяции?

5. В чем состоит различие сплайн – интерполирования от обычной интерполяции?