
- •Иркутского государственного технического университета
- •2202 “Автоматизированные системы обработки информации и управления ”
- •Раздел 1 Погрешности вычислений
- •Причины возникновения погрешностей
- •Лабораторная работа 1
- •Вспомогательные материалы
- •5.1 Разработка программы в MathCad
- •Раздел 2 Численные методы решения систем линейных алгебраических уравнений
- •Решение систем линейных алгебраических уравнений методом Гаусса
- •Решение систем линейных алгебраических уравнений методом итераций
- •Лабораторная работа 2 Решение систем линейных алгебраических уравнений методом Гаусса
- •Вспомогательные материалы
- •Пример программы в MathCad
- •Лабораторная работа 3 Решение систем линейных алгебраических уравнений методом итераций
- •Раздел 3 Решение нелинейных уравнений
- •Итерационный метод решения нелинейных уравнений
- •Лабораторная работа 4 Решение нелинейных уравнений
- •Раздел 4
- •1. Первая интерполяционная формула Ньютона
- •3. Оценки погрешностей интерполяционных формул Ньютона
- •4. Интерполяционная формула Лагранжа
- •6 Обратное интерполирование
- •Блок-схема программы построения кубического сплайна и построения полинома Лагранжа представлены на рис. 4.3 и рис. 4.4
- •Лабораторная работа 5 Методы интерполирования функций
- •Раздел 5
- •Квадратурные формулы интерполяционного типа (формулы Ньютона - Котеса)
- •Формула прямоугольников
- •Формула трапеций
- •Формула Симпсона
- •Оценка погрешности квадратурных формул
- •Квадратурные формулы Гаусса
- •Блок-схемы решения задачи рассмотренными методами приведены на рис. 5.4 и 5.5.
- •Лабораторная работа 6 Методы численного интегрирования
- •Раздел 6 Численное решение обыкновенных дифференциальных уравнений
Министерство образования и науки Российской Федерации
Иркутский государственный технический университет
Ю.П. Хрусталев
ОСНОВЫ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ
Практикум
Для студентов, обучающихся по специальностям:
: 2201 “Вычислительные машины, комплексы, системы и сети ”
2202 “Автоматизированные системы обработки информации и управления ”
719 «Информационные системы в технике и технологиях»
Издательство
Иркутского государственного технического университета
2009
Рецензент – начальник отдела ИСЭМ СО РАН, д.т.н. профессор В.И. Зоркальцев
Основы вычислительной математики. Практикум. Разработал доцент кафедры вычислительной техники Ю.П. Хрусталев – Иркутск, 2008 – с 94
Рассмотрены методы вычислительной математики. Проведен анализ погрешностей, возникающих при выполнений приближенных вычислений.
Приведены алгоритмы решения основных задач вычислительной математики и показана методика их реализации с помощью системы MATHCAD.
Для студентов, обучающихся по специальностям:
: 2201 “Вычислительные машины, комплексы, системы и сети ”
2202 “Автоматизированные системы обработки информации и управления ”
719 «Информационные системы в технике и технологиях»
Библиография – Назв. – 7 Табл. – 6 http://detc.usu.ru/Assets/aMATH0021/l1_3.htm
ОГЛАВЛЕНИЕ
1. Раздел 1. Погрешности вычислений Стр. 4
2. Раздел 2. Численные методы решения систем линейных
алгебраических уравнений Стр. 14
3. Раздел 3. Решение нелинейных уравнений Стр. 40
4. Раздел 4. Интерполирование функций Стр. 46
5. Раздел 5. Численное интегрирование Стр. 65
6. Раздел 6. Численные методы решения обыкновенных
дифференциальных уравнений Стр. 85
Раздел 1 Погрешности вычислений
Краткое введение. Большинство величин, с которыми приходится встречаться в практике, являются приближенными, т.е. такими, точное значение которых неизвестно. Оценкой приближения такой величины к точному значению является погрешность, или ошибка. В практике используют абсолютные и относительные погрешности.
Абсолютная погрешность ε - это разность между истинным и приближенным значением величины:
![]() (1)
(1)
Относительная погрешность - это отношение величины абсолютной погрешности к приближению:
![]() (2)
(2)
Для
величин, близких по значению к единице,
абсолютная и относительная погрешности
имеют один порядок. Для очень больших
и очень маленьких величин эти погрешности
существенно отличаются. Например, если
точное значение некоторой величины
равно 0.00006, а приближенное значение
0.00005, то
![]()
![]() =
=![]() ,
а
,
а
![]() (20%).
Если точное значение величины равно
100500, а приближенное 100000, то
(20%).
Если точное значение величины равно
100500, а приближенное 100000, то
![]() ,
а
,
а
![]() .
.
Если с приближенными значениями проводить различные арифметические действия, то в результате получится приближенная величина, погрешность которой будет зависеть от погрешностей исходных величин и , как правило, будет больше этих величин. Погрешности будут вычисляться следующим образом:
СЛОЖЕНИЕ (ВЫЧИТАНИЕ)
![]()
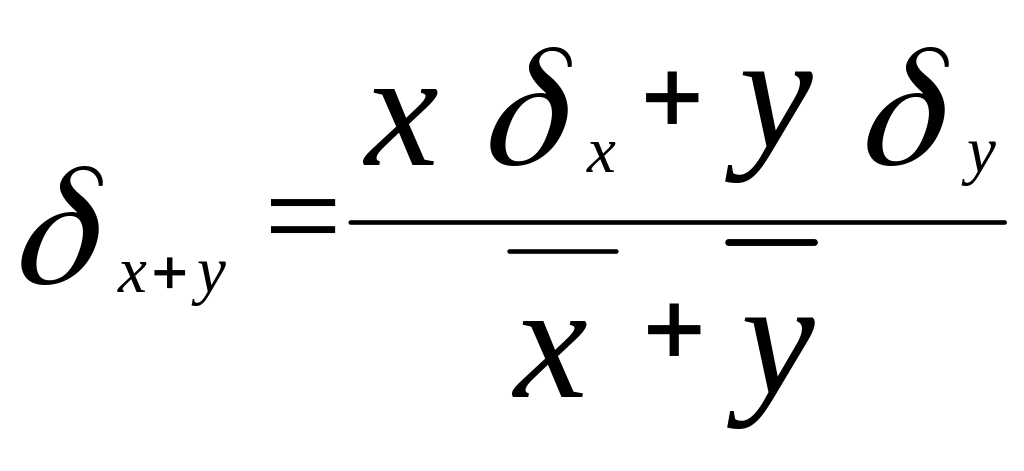 (3)
(3)
УМНОЖЕНИЕ
![]()
![]() (4)
(4)
ДЕЛЕНИЕ
![]()
![]() (5)
(5)
Для уменьшения погрешности в практической деятельности рекомендуется соблюдать следующие правила:
По необходимости избегать вычитания двух почти равных чисел.
Использовать формулы типа
a(b-c) = ab -ac ; (b-c)/a = b/a - c/a.
