3. Оценки погрешностей интерполяционных формул Ньютона

Если узлы интерполирования - равноотстоящие причем то , пологая , получим остаточные члены для 1-ой и 2-ой интерполяционных формул Ньютона:

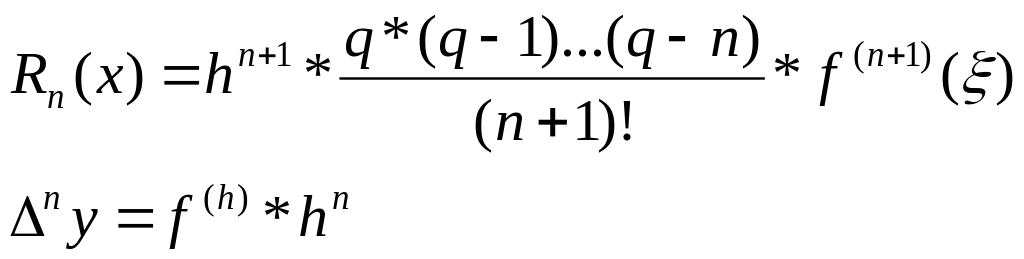(10)

, (11)

Где - некоторое промежуточное значение между узлом интерполирования и точкой .

(Для интерполирования , для экстраполирования возможно, что ).

При расчетах порядок n разностей выбирается таким, что . Учитывая, что h достаточно мало и и что

можно положить:

(12)

При этом остаточные члены интерполяционных формул Ньютона будут равны

Пример: В пятизначных таблицах логарифмов даются логарифмы целых чисел от х=1000 до х=10000 с предельной абсолютной погрешностью, равной . Возможно ли линейное программирование с той же степенью точности?

Решение: Т.к. , то где

Отсюда

, а

Из формулы (1) при n=11 и h=1 получаем:

Т.к. (интерполируем не далее, чем на 1 шаг), то

Окончательно получаем:

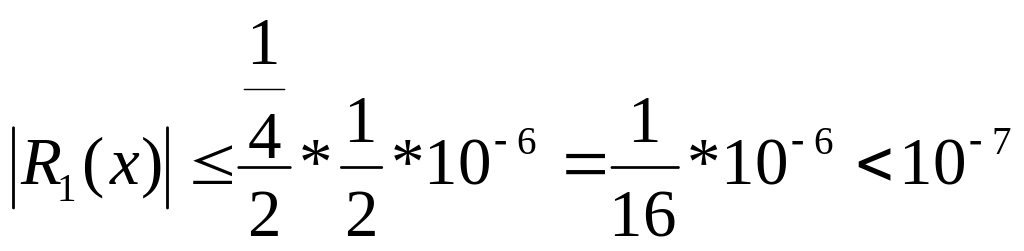
Т.о. погрешность интерполирования не превосходит погрешностей исходных данных!

Линейное интерполирование (h=1) возможно.

Интерполяционные формулы Ньютона используют лишь значения функций, лежащие лишь по одну сторону от выбранного начального значения Для интерполирования в середине таблицы удобно применять формулы, содержащие как последующие, так и предшествующие значения функций по отношению к начальному ее значению.

При этом используются центральные разности

Интерполяционные формулы, построенные с помощью центральных разностей - это формулы Гаусса, Стирлинга, Бесселя.

4. Интерполяционная формула Лагранжа

Для произвольно заданных узлов интерполирования (в том числе и для неравноотстоящих узлов ) применяется интерполяционная формула Лагранжа.

П усть на отрезке [a, b] задано n+1 значений аргумента и известны значения функций y=f(x):

Требуется построить полином степени не выше n, имеющий в заданных узлах , те же значения, что и функция f(x), т.е. такой,

Рис. 4.2 Построение полинома

что

Рассмотрим частную задачу: построить полином , такой, чтобы = 0

при и при

Т.е. (13)

Такой полином имеет вид:

(14)

При в силу условия (13),

поэтому

И

В результате получаем:

(15)

Будем теперь искать интерполяционный полином в виде

Этот полином имеет вид:

(16)

Подставляя (15) в (16), получаем:

(17)

Это и есть интерполяционная формула Лагранжа

При n=1 имеем:

- уравнение прямой,

проходящей через 2 заданные точки: (

При n=2 получаем уравнение параболы, проходящей через три точки:

(точки

Пример: Для функции построить интерполяционный полином Лагранжа, выбрав узлы:

Решение: Вычисляем

По формуле (17) получаем:

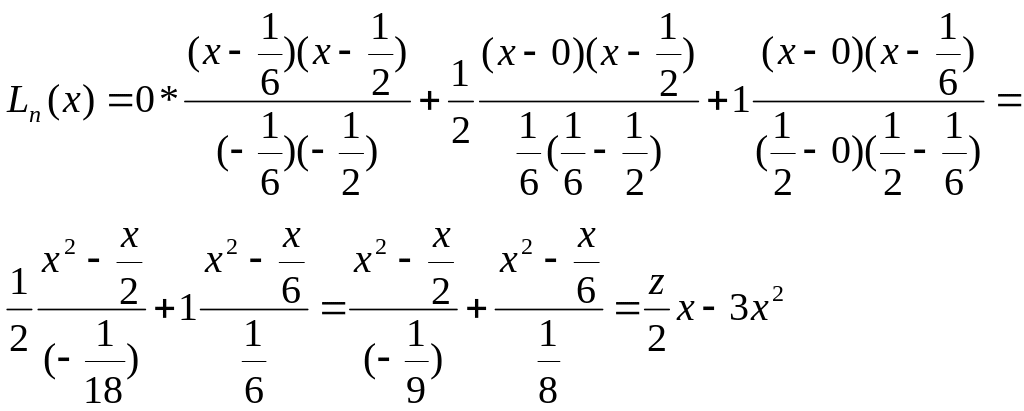
Точность не велика, т.к. синусоиду мы интерполируем квадратичной параболой.

`5. Оценка погрешности интерполяционной формулы Лагранжа

(18)

где

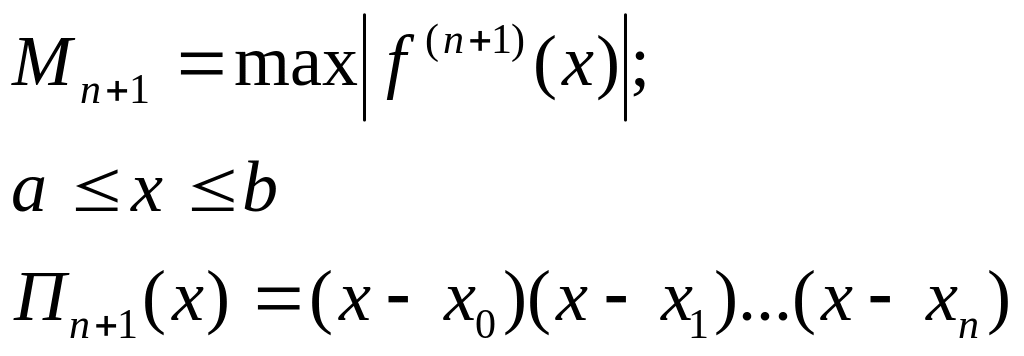
Пример: с какой точностью можно вычислить с помощью интерполяционной формулы Лагранжа для функции , выбрав узлы интерполирования Три точки n=2.

Решение: имеем

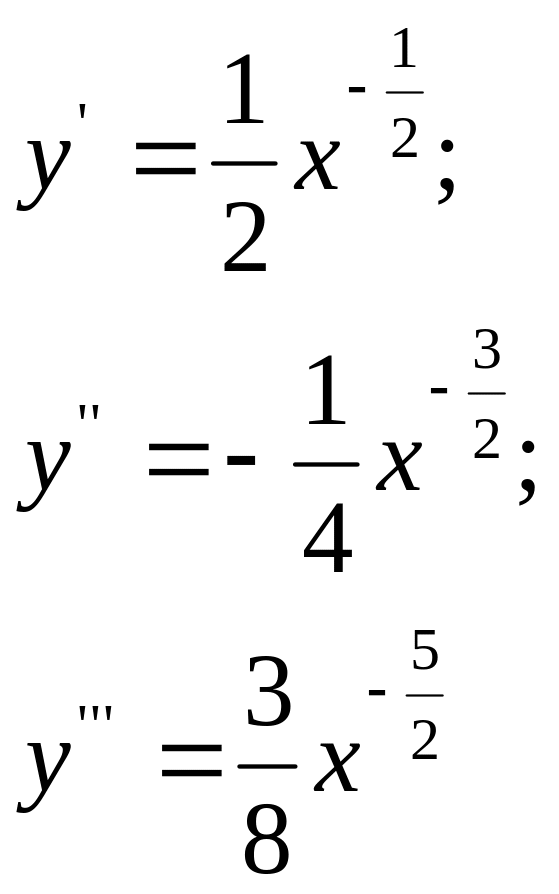Отсюда (т.к.

Из формулы (18) получаем: