Лабораторная работа 2 Решение систем линейных алгебраических уравнений методом Гаусса

Работа выполняется с использованием палитры программирования системы автоматизации математических вычислений Mathcad

Задание на работу:

1. Разработать программу для решения системы линейных алгебраических уравнений методом Гаусса с выбором главного элемента по столбцам.

2. Решить систему уравнений, определенную вариантом задания.

3. Произвести проверку решения.

4. Изменить матрицу коэффициентов А, сделав систему уравнений линейно зависимой, и проверить работоспособность программы в этом случае.

Варианты заданий .

( Система уравнений в матричной записи имеет вид Ax = b)

1. A=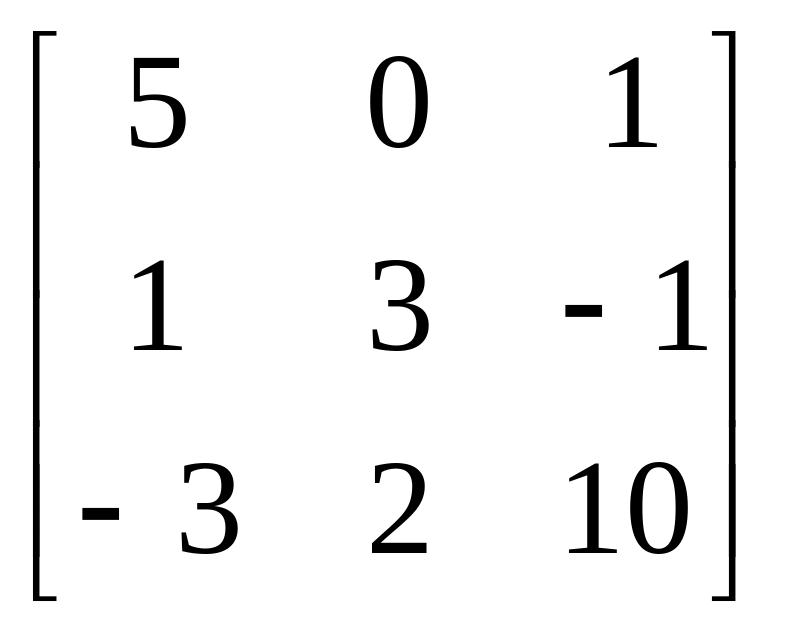 , b= 2. A= , b=

3. A= , b= 4. A= , b=

5. A= , b= 6. A= , b=

7. A= , b= 8. A= , b=

9. A= , b= 10. A= , b=

11. A= , b= 12. A= , b=

13. A= , b = 14. A= , b=

15. A= , b = 16. A= , b=

17. A= , b = 18. A= , b=

19. A= , b = 20. A= , b=

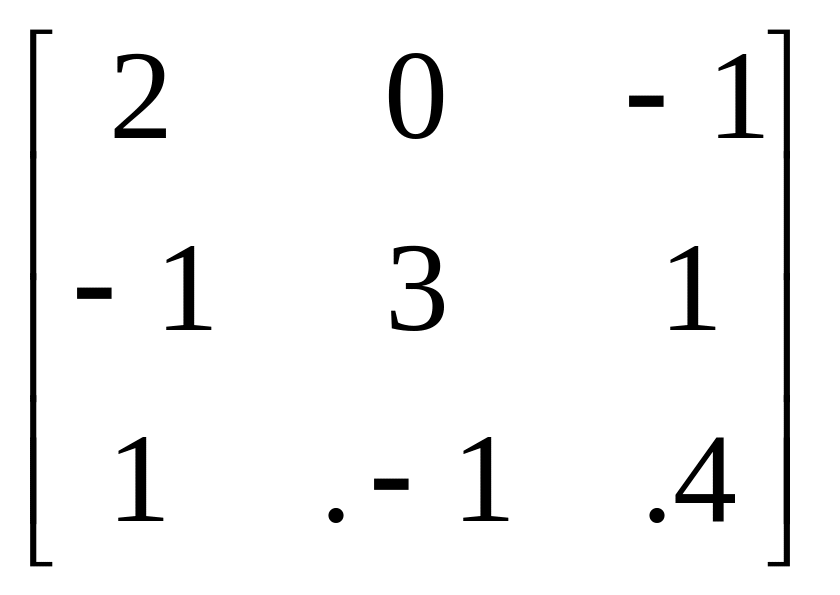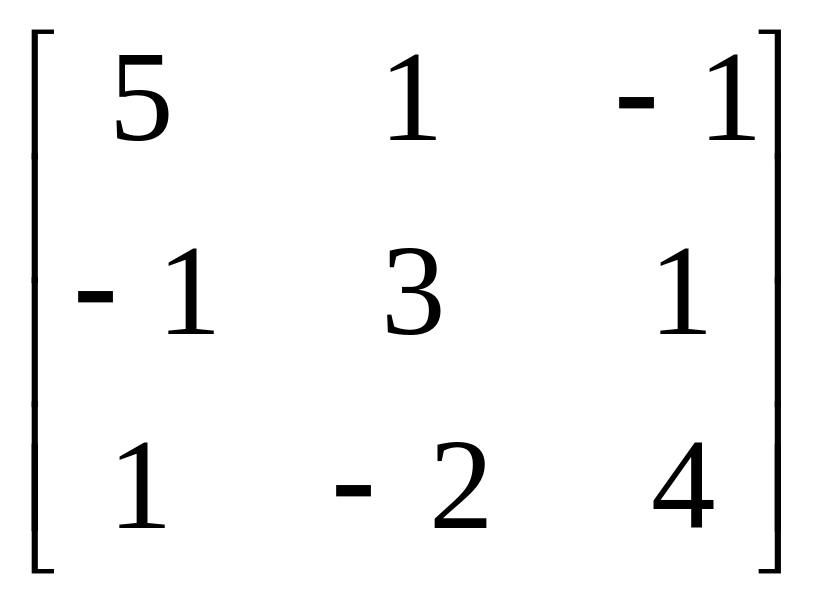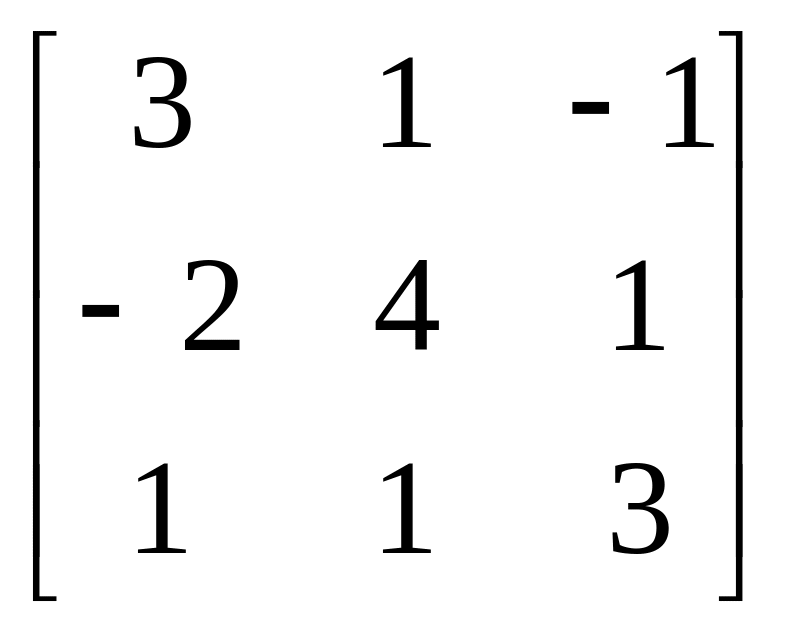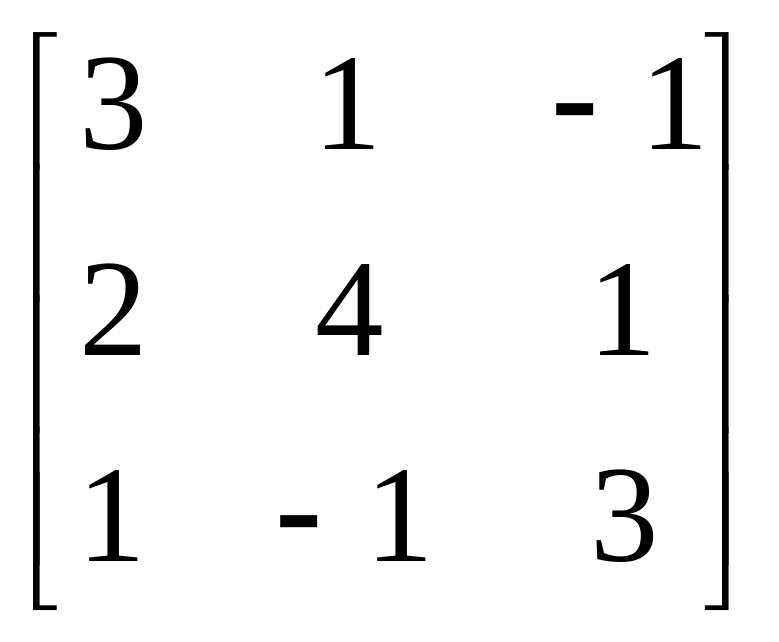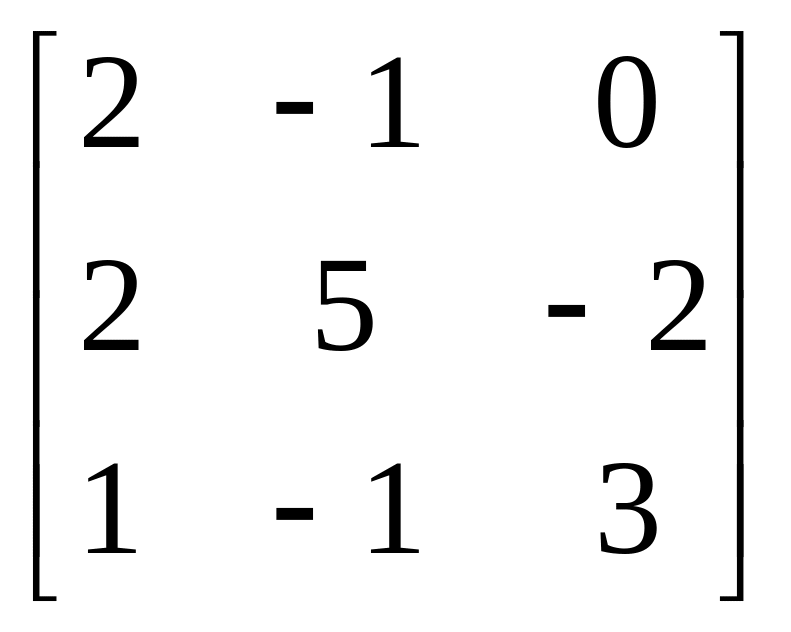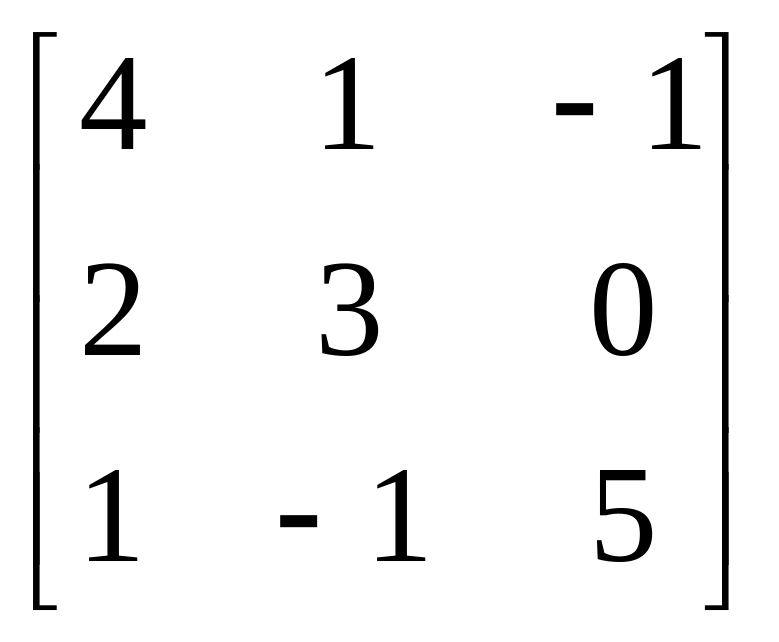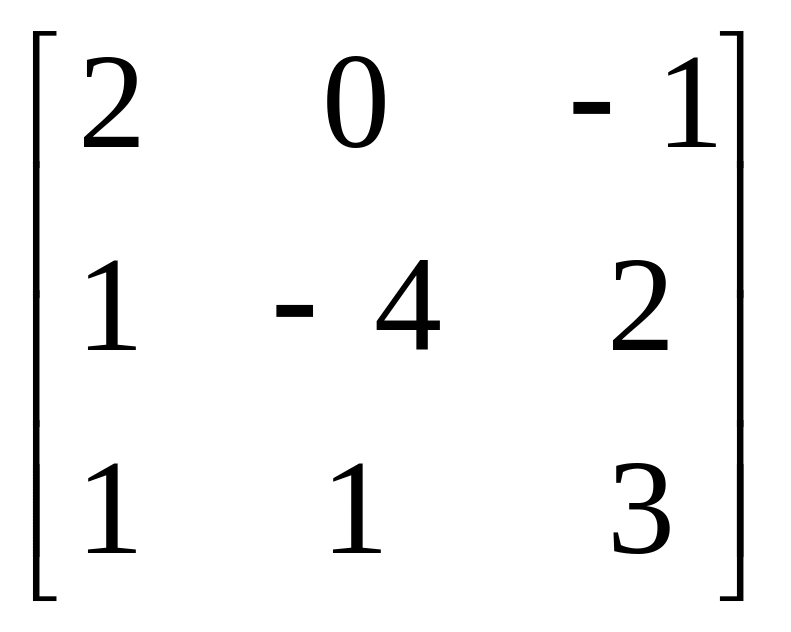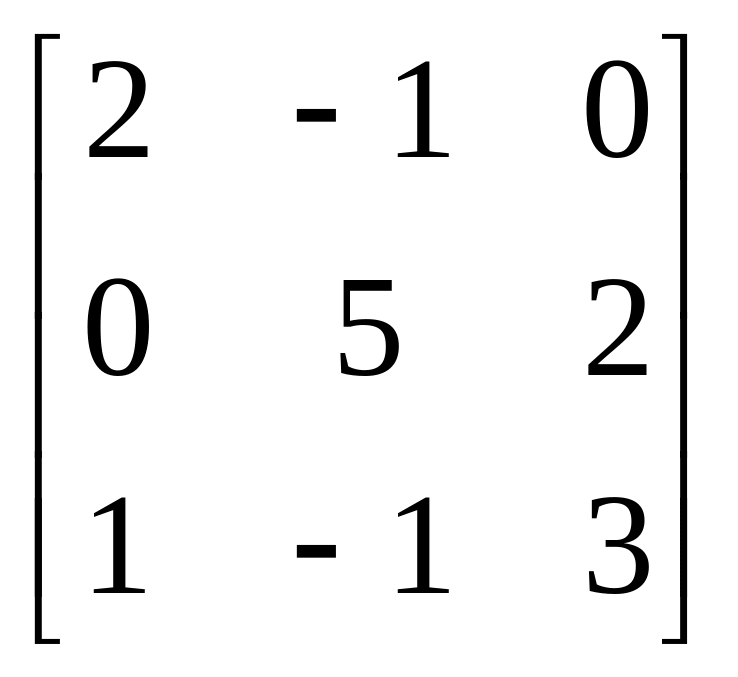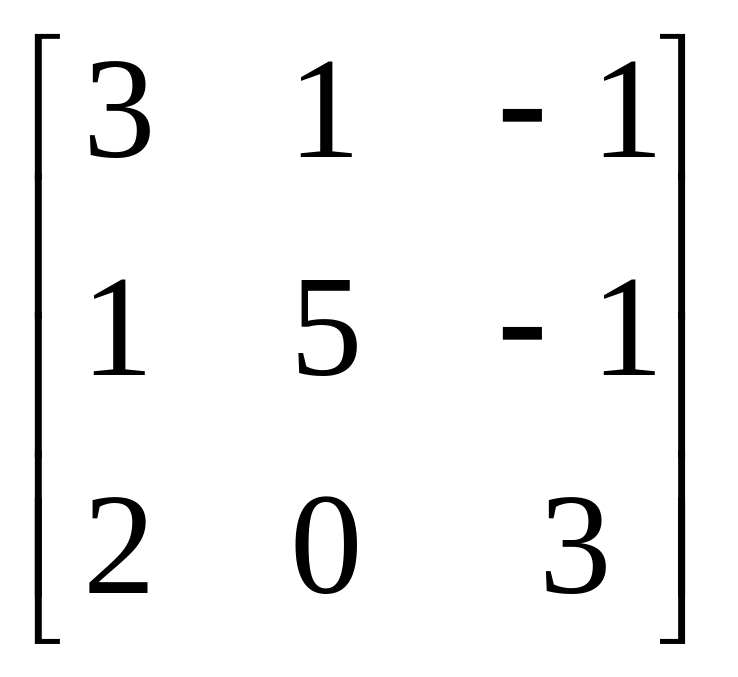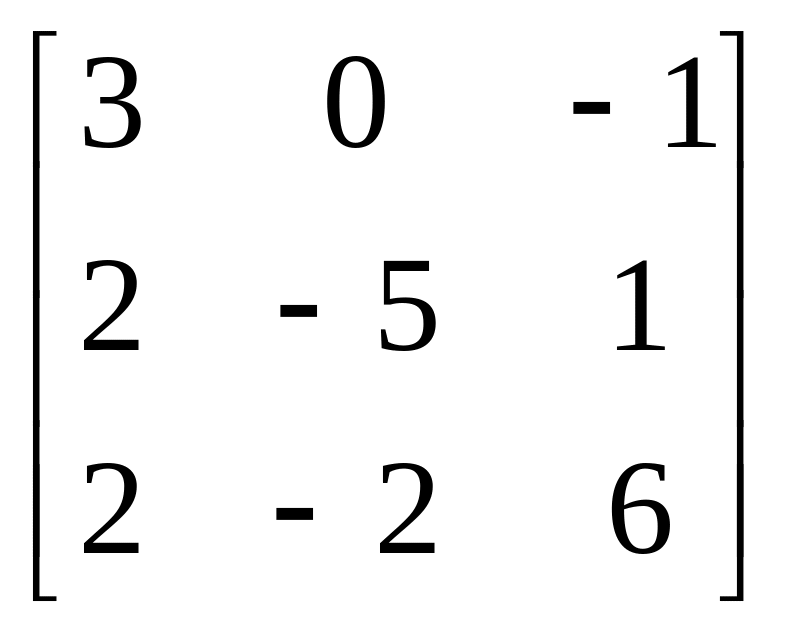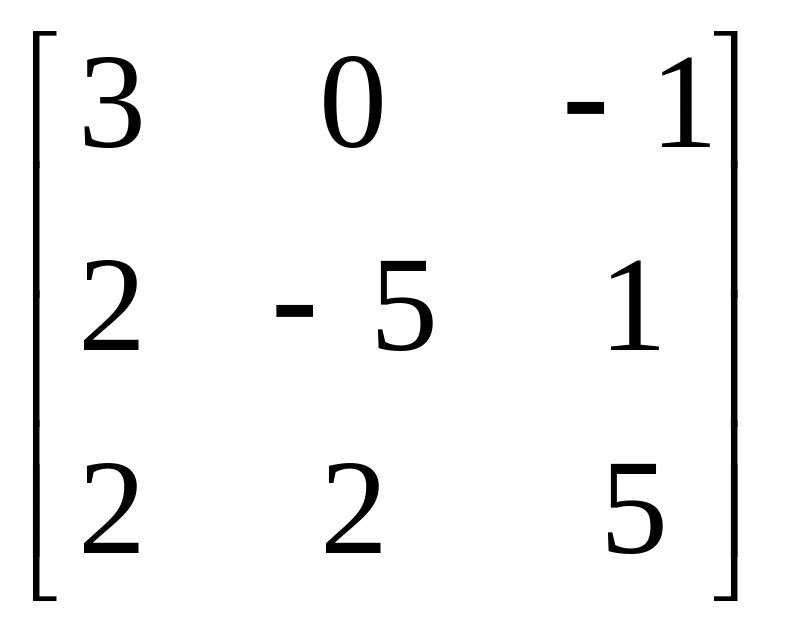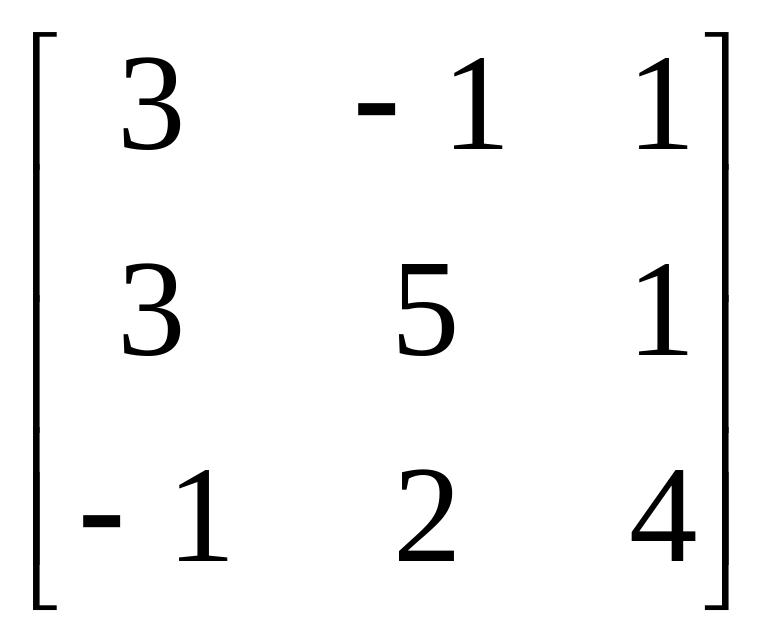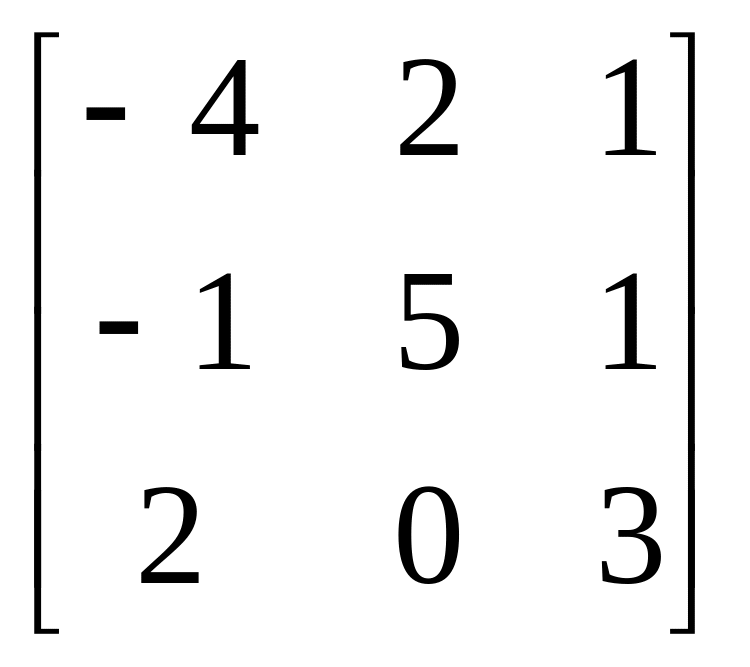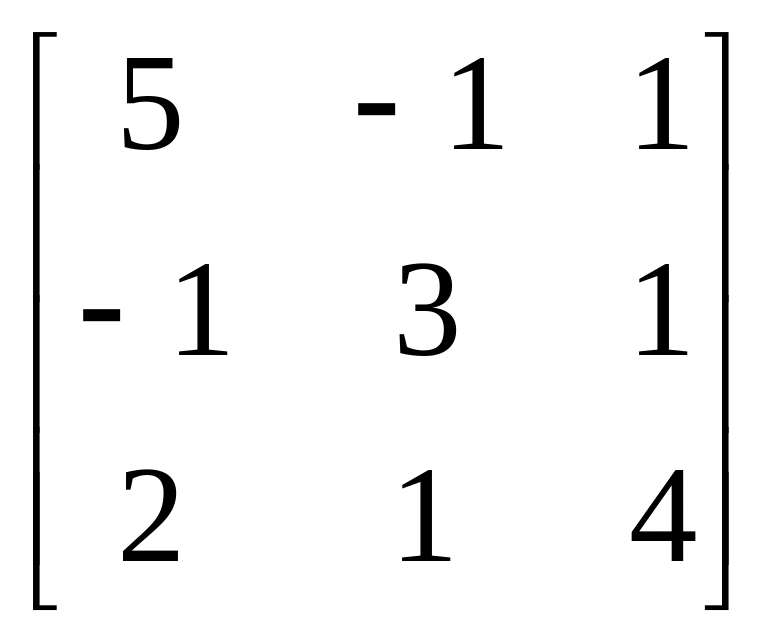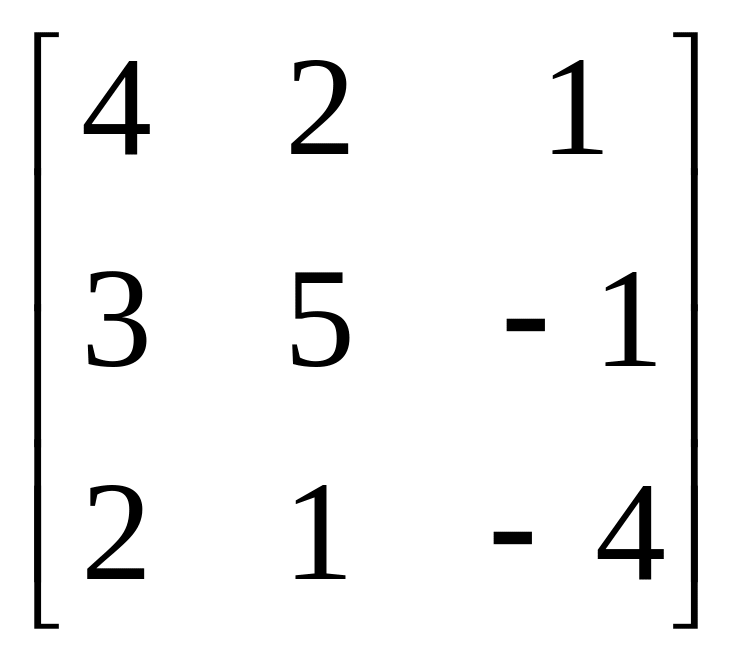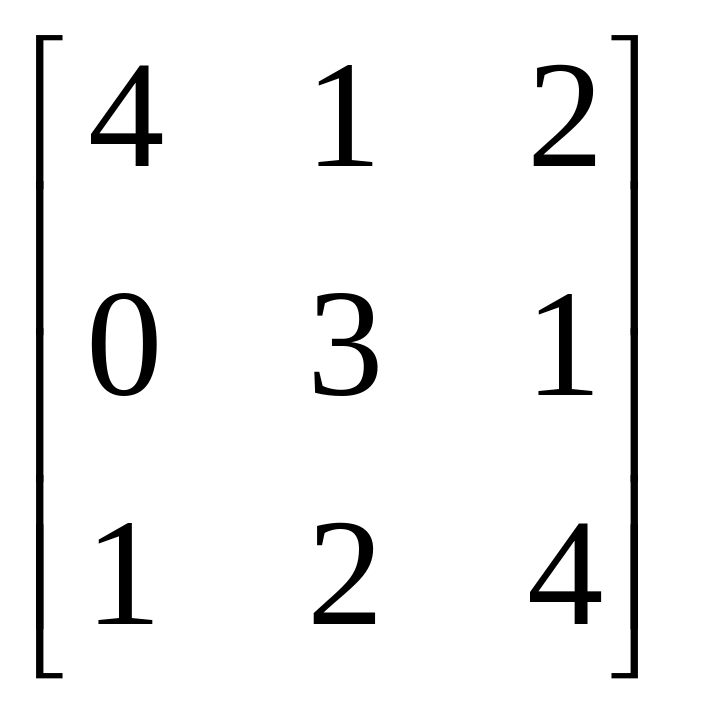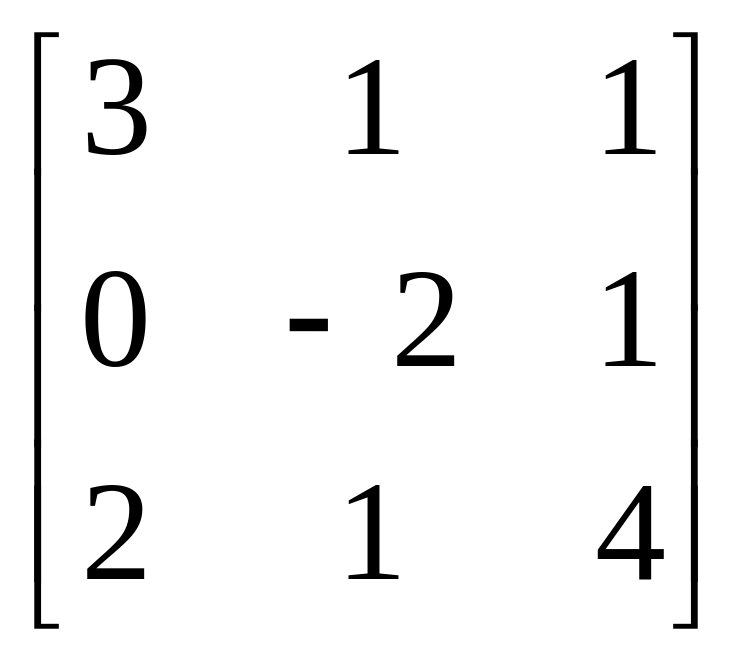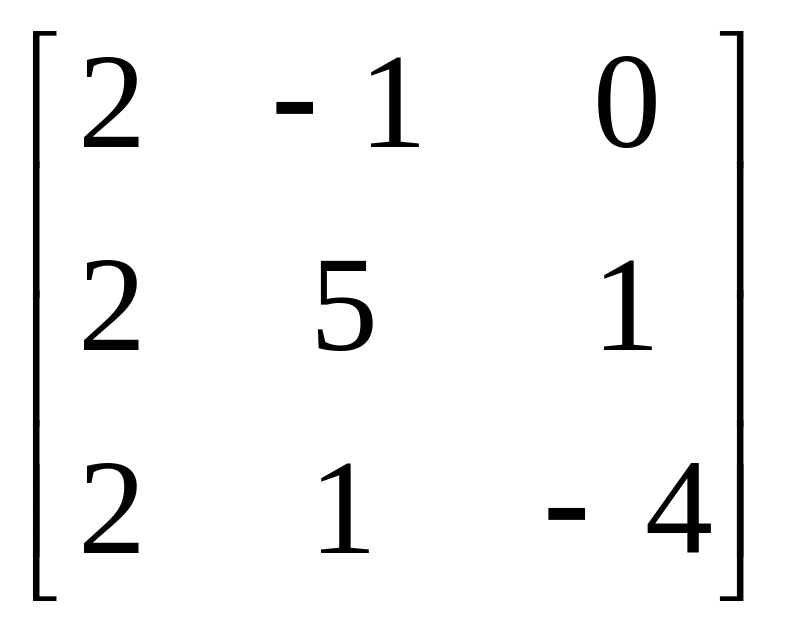21. A= , b =

Требования к оформлению отчета

Отчет должен содержать:

• Название и цель работы

• Задание на работу

• Текст программы на Mathcadе

• Результаты работы программы

• Проверку решения

Вспомогательные материалы

Пример разработки программы для решения системы линейных агебраических уравнений в системе Mathcad

Этап 1. Объявление переменных

Определим переменные и зададим матрицу системы линейных уравнений:

С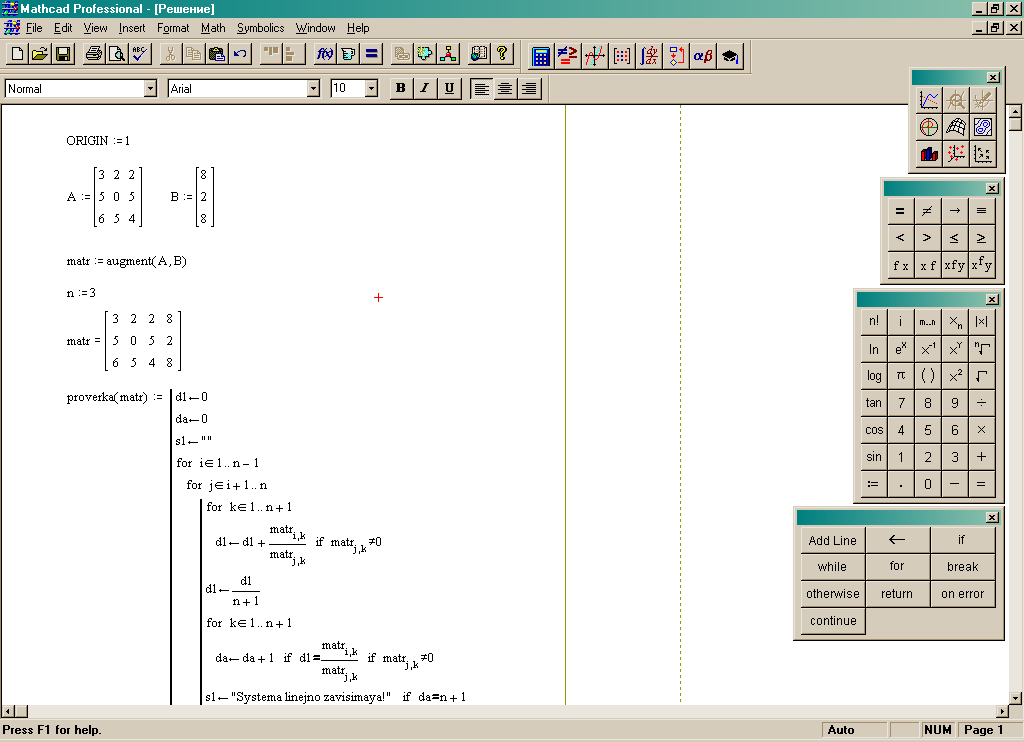 оздадим новый лист в MathCAD и для начала напишем оператор ORIGIN := 1 – это для того чтобы MathCAD начинал нумерацию в матрицах с 1, а не с нуля.

Теперь определим матрицу А.

Обратите внимание, что в MathCAD строчные и прописные буквы различны, следите за регистром переменных.

Наберите A:= нажмите меню Insert  Matrix задайте размерность матрицы 3 на 3 и нажмите OK. Заполните матрицу как показано на рисунке. Тем же способом задайте матрицу-столбец B.

Объединим все в одну расширенную матрицу matr с помощью оператора augment.

Присвоим переменной n значение 3, она будет определять количество корней системы.

Чтобы посмотреть значение любой переменной, достаточно написать ее имя и поставить знак равенства. Выведем значение переменной matr.

Еще одной важной особенностью MathCAD является последовательность операторов, например, если мы попробуем написать выражение matr:=augment(A,B) перед определением матриц A и B, то MathCAD выдаст ошибку.

Переменные определены, теперь перейдем к написанию функции проверки матрицы на линейно-зависимые строки.

Этап 2. Проверка на линейно-зависимые строки

На языке Pascal эта процедура будет выглядеть так:

Function Proverka(): boolean;

var d1: single;

da: word;

lin: boolean;

begin

d1:=0;

da:=0;

lin:=False;

For i:=0 to n-2 do

For j:=i+1 to n-1 do

Begin

For k:=0 to n-1 do

If matr[j,k]<>0 then d1:=d1+matr[i,k]/matr[j,k];

d1:=d1/n;

For k:=0 to n-1 do

If matr[j,k]<>0 then If d1=matr[i,k]/matr[j,k] then da:=da+1;

If da=n then lin:=True;

d1:=0;

da:=0;

end;

If lin then Proverka:=True Else Proverka:=False;

e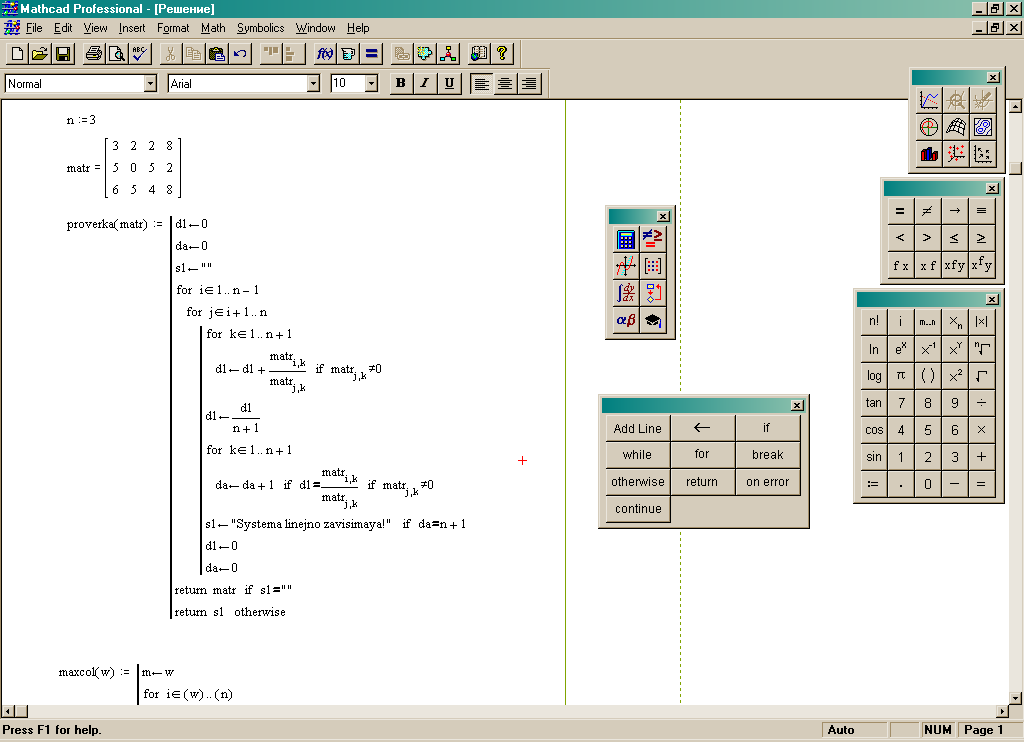 nd;

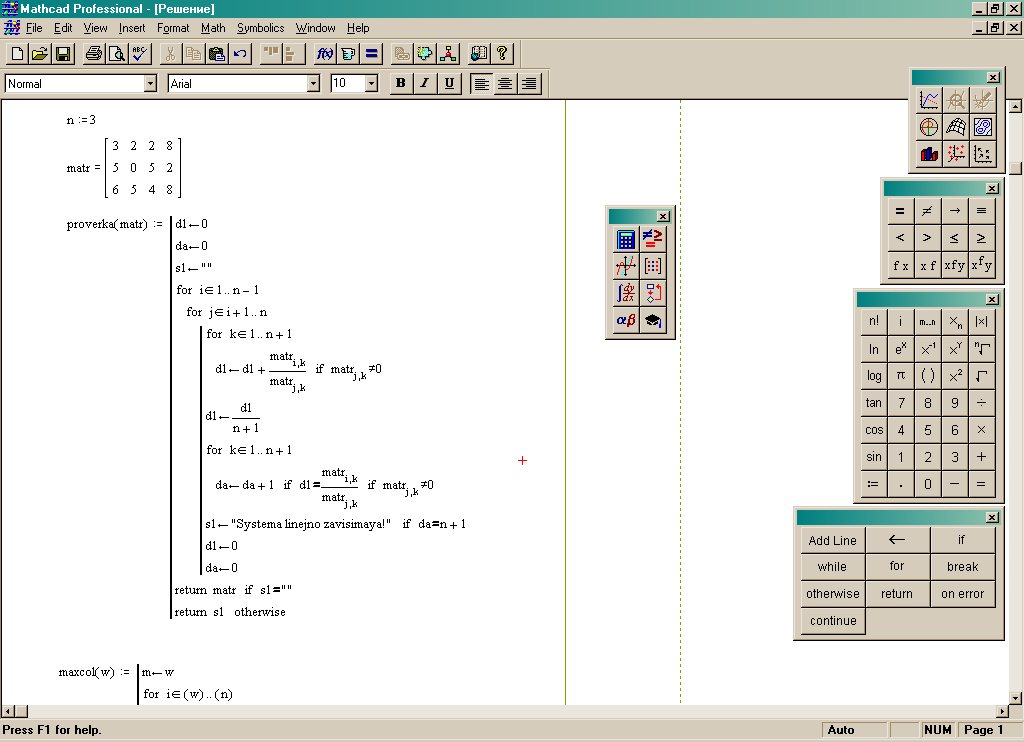
Проверка на линейно-зависимые строки в Mathcadе

О

Рис 2.3

Рис 2.4

ткройте панель, изображенную на рисунке 2.3. С помощью меню view  Math Palette. Щелкните на третьей строке во втором столбике иконки и перед вами откроется еще одна панель инструментов (рис. 2.4), отвечающая за встроенный язык программирования.

Так же в процессе решения нам понадобятся еще некоторые панели инструментов рис.2.5 и рис.2.6.

Найдите их на панели Math Palette (рис.2.3).

О

Рис 2.6

ператор Add Line обозначает в MathCAD программный модуль - вертикальную черту, справа от которой последовательно записываются операторы.

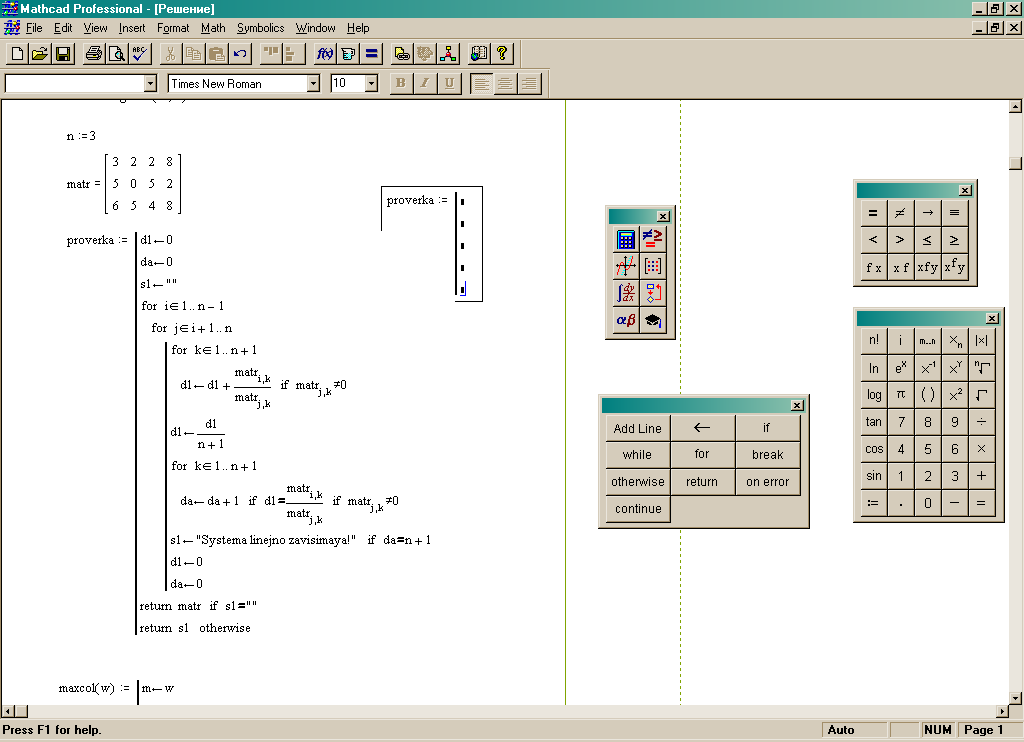О ператор  означает присваивание: F  2+B

Otherwise – это оператор аналогичный Else в Pascal. С остальными операторами, думаю, вы знакомы.

Н

Рис 2.5

Рис 2.7

апишем имя функции, оператор присваивания и вставим программный модуль, несколько раз нажав кнопку Add Line на панели программирования, вот что должно получиться (рис. 2.7).

Определим локальные переменные:

Еще одной особенностью языка MathCAD является то, что он сам определяет тип переменных.

d1 – будет хранить результат деления строк матрицы.

da – будет хранить количество совпавших элементов деления.

s1 – для хранения сообщения и результата проверки. (в Pascal эта переменная lin)

Теперь нам нужно разделить все строки между собой друг на друга и определить общее частное. Легче всего это сделать, разделив поочередно сначала первую строчку на все другие, затем вторую на оставшиеся и т.д.

Запишем это так:

i будет обозначать делимое, а j делитель.

Совет. Чтобы вставить последовательность 1..n-1 нажмите на панели инструментов.

Внимание! Не вводите с клавиатуры имена программных операторов. Для их вставки с клавиатуры можно применять лишь сочетания клавиш, которые приведены в тексте всплывающей подсказки.

Рис 3.

В тело цикла вставьте Add Line и вставим еще один цикл для того, чтобы найти сумму всех частных. Следует учитывать ситуацию деления на ноль, поэтому ограничим действия с помощью условного оператора if.

Обратите внимание! Что в MathCAD оператор if записывается, наоборот, в отличие от записи в Pascal. Т.е. сначала действие, которое произойдет, если выполниться условие.

Следующим шагом найдем среднее от частного, разделив на число слагаемых n и присвоив это значение d1.

Т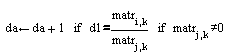 еперь проверим, сколько слагаемых равны d1. Переменную da будем увеличивать на единицу, если условие верно. Так же как и в предыдущем случае не стоит допускать деления на ноль, поэтому здесь используется вложенный оператор if.

После выполнения цикла, проверим, равно ли da = n, если так, то эти строки линейно зависимые.

Пример:

Допустим, матрица выглядит так: .

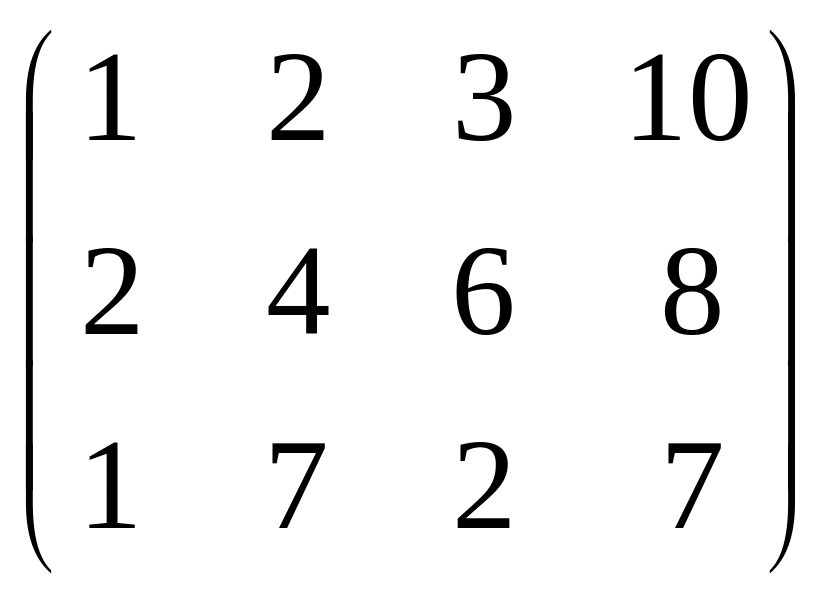d1 будет равно = 1/2+2/4+3/6= 1.5

d1 = 1.5 / n = 1.5 / 3 = 0.5

d1 = 1/2 = 2 /4 = 3/6 = 0.5 , то da = 3 и равно n, значит строки линейно-зависимые.

Далее установим значение переменных da и dl на ноль. Чтобы гарантировать нормальную работу алгоритма при следующих итерациях.

Возвратим результат функции. Если значение строковой переменной s1 так и не изменилось, то возвратим матрицу matr, в противном случае выведем сообщение наличии линейной зависимости.

Этап 3. Нахождение максимального элемента в столбце

Для реализации модифицированного метода Гаусса нам понадобиться функция нахождения максимального элемента в столбце и возвращение номера строки этого элемента.

Алгоритм этой функции достаточно прост и не требует подробных объяснений.

Этап 4. Перестановка строк в матрице

После того как найдена строка с максимальным элементом в столбце, возможно, нам понадобиться поменять эти строки местами. Для этого создадим функцию:

Определим переменные: i1 будет использоваться в цикле, а temp для временного хранения элементов матрицы. Далее цикл и стандартный алгоритм замены переменных.

Возвратим матрицу matr.

Этап 5. Прямой ход

Все дополнительные функции определены, теперь можно перейти непосредственно к поиску решения. Выполним прямой ход в методе Гаусса:

Определим некоторые переменные: i1 будет использоваться в цикле, а s1 для хранения сообщения о том, что система не имеет единственного решения. Создадим главный цикл.

Первым делом найдем строку с максимальным элементом через ранее объявленную функцию maxcol и присвоим это значение переменной max. Чтобы застраховать себя от частного случая, проверим, не является ли максимальный элемент равным нулю, если это так, то система не имеет единственного решения, и выйдем из цикла, используя команду break. В Pascal сразу произведем замену Zamena (i1,MaxCol(i1)) и реализуем алгоритм проверки в теле функции maxcol:

В MathCAD :

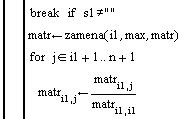
Если все в порядке, то поменяем строки местами.

Получим разрешающее уравнение, разделив каждый элемент на первый в строке i1

Получим:

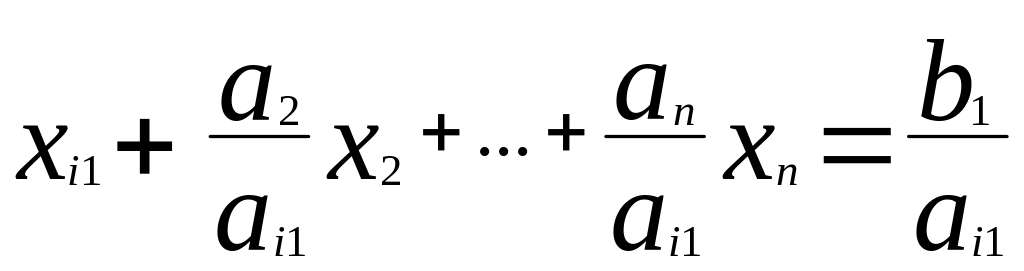
П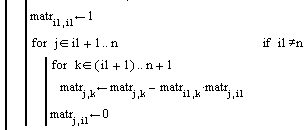 рисвоим единицу коэффициенту при x_i1

Умножим разрешающее уравнение i1 на первый коэффициент уравнения j и вычтем полученное из уравнения j.

Присвоим ноль коэффициенту при х_j,i1

После выполнения всех итераций матрица примет треугольный вид, теперь не сложно найти корни системы.

Н о не забудьте возвратить преобразованную матрицу или, в случае, если система не имеет единственного решения, соответствующее сообщение.

Этап 6. Обратный ход

Теперь не составит труда найти корни уравнения, выполнив обратный ход. Напишем еще одну функцию oh:

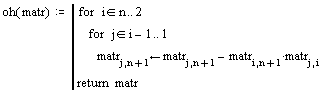
Выполним обратный цикл, задав диапазон значений от n до 2, где n >= 2.

Тем самым пройдем по строкам в обратном порядке.

Далее, еще один цикл, чтобы пройти по всем элементам строки, от последнего до первого. Последовательно исключив неизвестные переменные, получим в последнем столбце матрицы корни уравнения.

Задача решена, осталось только вывести результаты.

Этап 7. Вывод ответа

С оздадим матрицу-столбец a из последнего столбца матрицы matr и возвратим ее.

Соберем все воедино в функции otvet:

1. Выполним проверку на линейную зависимость.

2. Выполним прямой ход, если значение matr удовлетворяет условию.

3. Затем обратный ход с аналогичной проверкой.

4. И присвоим matr полученный результат.

5. Вернем значение функции (им может быть или матрица-столбец с корнями системы или одно из двух сообщений)

В заключении выведем ответ, набрав otvet =. Ответ может быть трех типов:
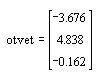