
- •Глава 1. Основные объекты исследования в логистике 4
- •Глава 2. Основы методологии и организация логистики 24
- •Глава 3. Закупочная логистика 47
- •Глава 4. Производственная логистика 74
- •Глава 5. Распределительная логистика 97
- •Глава 6. Логистика запасов 117
- •Глава 7. Логистика складирования 153
- •Глава 1. Основные объекты исследования в логистике
- •1.1. Происхождение термина и краткая история развития логистики
- •1.2. Определение логистики. Эволюция логистики, этапы ее развития
- •1.3. Основные понятия логистики
- •1.4. Логистические системы
- •Вопросы для контроля знаний
- •Глава 2. Основы методологии и организация логистики
- •2.1. Содержание методологии логистики. Основные парадигмы логистики
- •2.2. Фундаментальные концепции управления как теоретическая база логистики
- •2.3. Общенаучные методы и подходы, используемые в логистике
- •2.4. Логистическая среда и ее факторы
- •2.5. Принципы логистики
- •2.6. Основные аналитико-прогностические методы, используемые в логистике
- •2.7. Организационные структуры управления логистикой
- •Вопросы для контроля знаний
- •Глава 3. Закупочная логистика
- •3.1. Цели, задачи и содержание закупочной логистики
- •3.2. Определение общего объема входящего материального потока
- •3.3. Планирование материальных потоков в разрезе поставщиков
- •3.4. Определение параметров партий поставок
- •3.5. Контроль входных материальных потоков
- •Вопросы для контроля знаний
- •Глава 4. Производственная логистика
- •4.1. Сущность и содержание производственной логистики
- •4.2. Базовые логистические концепции управления производственными процессами в организации
- •4.3. Микрологистическая система «Lean production»
- •4.4. Перспективы развития логистических систем в производстве
- •Вопросы для контроля знаний
- •Глава 5. Распределительная логистика
- •5.1. Сущность, задачи и функции распределительной логистики
- •5.2. Логистические каналы распределения, их виды и основные характеристики. Организация физического распределения продукции
- •5.3. Управление потоками в распределительной логистике. Обоснование построения системы распределения
- •5.4. Базовые и модифицированные логистические концепции управления процессами распределения
- •5.5. Экономико-математические методы и модели, используемые в распределительной логистике
- •Вопросы для контроля знаний
- •Глава 6. Логистика запасов
- •6.1. Место запасов в логистической системе
- •6.2. Цели, задачи и функции логистики запасов
- •6.3. Экономические проблемы логистики запасов
- •6.4. Стратегии управления запасами
- •6.5. Использование теории исследования операций для расчета оптимальных параметров системы запасообразования
- •6.6. Упрощенные методы расчета параметров системы запасообразования и управления ими
- •Вопросы для контроля знаний
- •Глава 7. Логистика складирования
- •7.1. Упаковка, тара, склад как объекты логистики
- •7.2. Условия и способы хранения продукции на товарном складе
- •7.3. Проектирование элементов склада
- •7.4. Логистический процесс на складе
- •7.5. Моделирование транспортно-складских операций
- •7.6. Выбор места расположения склада
- •Вопросы для контроля знаний
6.5. Использование теории исследования операций для расчета оптимальных параметров системы запасообразования
Многообразие экономико-математических методов планирования запасов предполагает их классификацию по различным признакам: типу исходной информации, критерию оптимизации; ассортиментному составу запасов; структуре системы снабжения; характеру процессов запасообразования (рис. 6.18).
При выборе метода оптимизации для практического использования основными критериями выступают максимально точное описание реальных процессов и доступность исходной информации. Массовое использование даже самых простых моделей возможно лишь с привлечением компьютерных технологий к под готовке исходной информации и расчетам и при соответствую щем программном обеспечении. Безусловно, практическую цен ность это будет иметь, если получаемая экономия финансовых средств превысит внедренческие и эксплуатационные затраты.

Классическая модель оптимизации запасов Уилсона (дегерминированные условия закупок и потребления) была пред ложена в 1915 г. и до настоящего времени остается актуальной. По сути она дала целое направление в исследовании операций и эптимизации запасов. Малое количество проблем описано в экономической литературе так подробно, как оптимизация объемов заказа. Появилось множество модификаций модели за счет включения дополнительных факторов. Усложнение затруднило ее практическое применение, поскольку для расчетов не всегда хватает необходимой информации. Вывод формулы основывается на необходимости минимизации затрат на закупку продуктов и их содержание на складе и классическом математическом анализе.
Движение запасов в общем случае выражается функцией, определяемой начальным запасом и условиями поступления и потребления продуктов. Аналитически оно выражается уравнением

Модели оптимизации запасов в той или иной форме основываются на этом простейшем балансовом уравнении. Варианты развивают и конкретизируют его, наделяя параметры поставок и отпусков определенными свойствами, и используют различные критерии управления запасами.
Классическая модель Уилсона позволяет установить оптимальные параметры управления запасами в идеальных условиях, когда все поставки имеют одинаковый объем и периодичность, потребление равномерно во времени, затраты по завозу одной партии не зависят от ее величины, а затраты по хранению единицы продукта — от общей величины запаса. Движение запаса в таких условиях характеризуется уменьшением его от максимального уровня, равного объему партии поставки, до минимального, равного нулю или сумме подготовительного и страхового запасов, перед очередной поставкой (рис. 6.19).
Эта модель позволяет рассчитать партию, периодичность поставок и норму текущего запаса, при которых достигается минимум затрат по содержанию запаса и организации завоза. Определяющим параметром выступает партия поставки, на основании которой рассчитываются два других оптимальных параметра.
Найти оптимальную партию поставки означает рассчитать ее величину, соответствующую минимуму целевой функции издержек И:

Расходы по хранению расчитываются исходя из средней величины находящегося на складе запаса и стоимости хранения его единицы в течение планового периода (года, квартала). Поскольку в данном случае речь идет о формировании запаса в элементарных условиях, то средний запас будет равен половине партии поставки:

Расходы, связанные с завозом продуктов, определяются как произведение стоимости завоза одной партии Сзав и количества поставок в плановом периоде n:

Такким образом, общая сумма затрат, связанных с образованием запасов, определяется поп формуле
![]()
В данной функции содержится единственная неизвестная величина Q, от которой зависит размер запаса. Задача заключается в минимизации функции затрат. Последняя дифференцируется относительно Q, а найденная производная приравнивается к нулю:
![]()
В результате решения уравнения получается формула оптимальной партии поставки, или формула Уилсона

Оптимальный
средний текущий запас
 составить половину этой партии:
составить половину этой партии:
![]()
Эти величины могут служить ориентиром при определении параметров договоров.
Как уже говорилось ранее, расчет удельных затрат по хранению запасов — занятие весьма трудоемкое, чаще их определяют экспертным путем в процентах к стоимости среднего запаса. В этом случае формула Уилсона незначительно модифицируется:
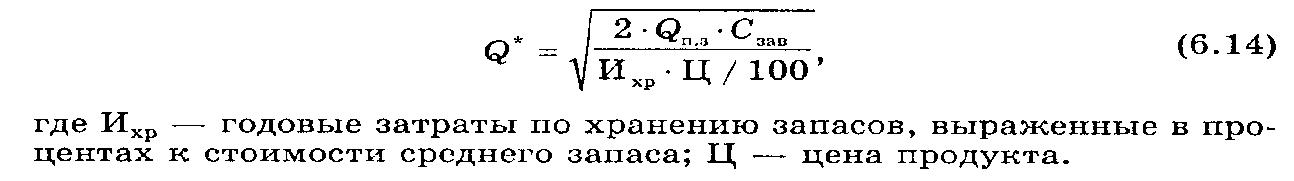

Модель Уилсона можно использовать не только в управлении поставками, но и при определении оптимальной партии запуска материалов в производство или отпуска товаров покупателю, когда величина запасов зависит в первую очередь от условий потребления продуктов. Расходы, связанные с организацией поставки, выступают в данном случае в форме издержек по переналадке оборудования или включают последние в свой состав наряду с другими статьями. Вместо объема поступления используется величина отпуска или объем производства.
Пример. Завод выпускает металлопрокат на одном и том же оборудовании. При переходе к выпуску другого типосорторазмера предприятие несет затраты по переналадке, равные в среднем 300 тыс. руб. Потребность в металлопрокате каждого типосорторазмера составляет 10 ООО т в год, издержки содержания сбытового запаса — 1 % стоимости продукции, находящейся в запасе. Требуется найти оптимальные партию запуска изделий в производство и величину текущего сбытового запаса, если себестоимость 1 т проката в среднем равна 15 ООО тыс. руб.

Несмотря на простоту, применение формулы Уилсона имеет ограничения, и для этого есть немало причин:
формула требует плановых значений годовой потребности в материалах или продуктах. На практике эти данные не всегда можно получить, в лучшем случае определяют квартальную потребность, однако этого недостаточно;
в течение года затраты по завозу и хранению, а также цена закупаемого продукта не могут оставаться неизменными, прежде всего из-за инфляции;
строгое соблюдение рассчитанной оптимальной партии также невозможно по ряду причин: а) из-за ограниченных производственной мощности собственных цехов, спроса и возможностей поставщика, которые могут оказаться больше или меньше оптимальной партии; б) ограниченной способности склада; в) ограниченных оборотных средств на закупку материалов или товаров у предприятия;
далеко не всегда система учета на предприятии позволяет, быстро и точно рассчитать входящие в формулу издержки.
В
последнем примере показана возможность
определения издержек содержания запаса
в процентах к его стоимости. Другим
вариантом, позволяющим избежать
трудоемкого учета этих издержек, является
расчет среднего значения соотношения
издержек завоза к затратам на хранение
в целом по складу, поскольку в формулу
Уилсона входит именно это соотношение.
Конечно, его величина зависит от того,
что за продукты хранятся на складе,
но если речь идет об универсальных
многоассортиментных складах, то она
стремится к постоянной величине
 ,
которую можно вычислить по фактическим
данным о поставках в предыдущих
периодах.
,
которую можно вычислить по фактическим
данным о поставках в предыдущих
периодах.
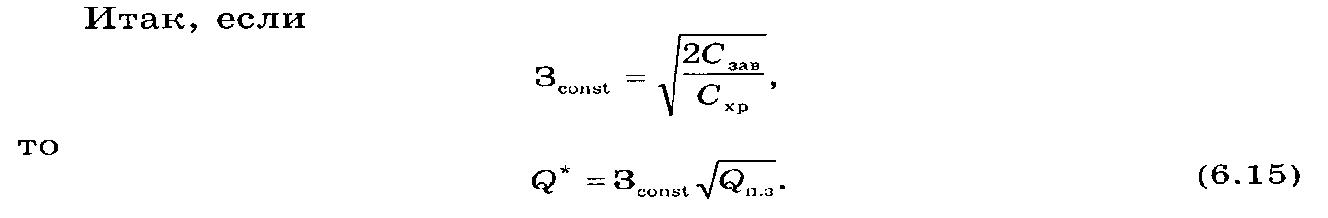
Предполагая, что условия поставок достаточно стабильны, запишем:

Наличие дефицита продуктов привносит особенности в модель Уилсона. Общий случай движения текущего запаса в условиях дефицита отражен на рис. 6.19.

Предполагается, что неудовлетворенный спрос откладывается и удовлетворяется по мере поступления продукта в организацию. Начальный запас 30 в условиях, допускающих дефицит, меньше Q. Дефицит равен разности Q - 30. Интервал времени т между двумя поставками делится на два участка: т1, когда на складе есть запас, и т2 — период дефицита.
Критерием оптимальности партии поставки и запаса в этих условиях являются минимальные суммарные затраты по хранению запаса, организации завоза и потери от дефицита:
![]()
Издержки, связанные с хранением запаса, могут быть рассчитаны по аналогии с классической моделью, однако с учетом того, что продукт находится в запасе лишь часть периода:

Потери из-за дефицита рассчитываются как дополнительные затраты, связанные с последствиями допущения среднего дефицита (Q-З0) / 2 в течение времени T2=T-T1:
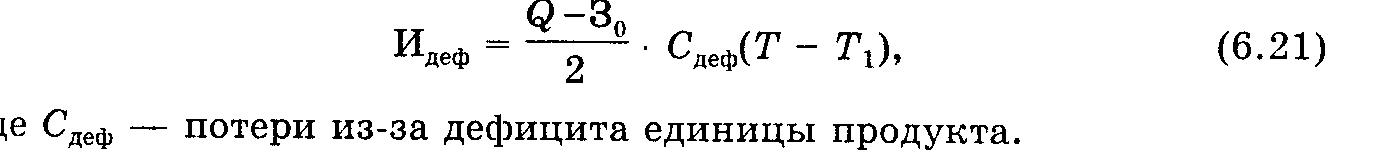
Расходы по завозу останутся теми же, что в элементарных условиях классической модели.
Общие затраты, таким образом, равны:
![]()
Поскольку Т жТх однозначно определяются исходя из среднесуточного расхода продукта и значений Зо и Q - Зо, то данная функция содержит две неизвестные — 3q и Q. Для ее оптимизации необходимо приравнять к нулю две частные производные по неизвестным, а затем решить систему двух уравнений. В результате получается следующая формула оптимального размера партии поставки в условиях дефицита:

Основой для построения вероятностных аналитических моделей управления запасами являются статические модели при случайном спросе на товар. Эти модели имеют и самостоятельную область применения в управлении сезонными запасами, запасами запчастей и скоропортящихся продуктов.
Организации, закупая уникальное оборудование, заказывают вместе с ним запасные части по цене Ц за единицу. Если запасных частей будет закуплено недостаточно, то в случае поломки оборудования организации понесут потери в размере Сдеф при нехватке одной запасной детали. Однако если во время эксплуатации оборудования запасные части не будут использованы, они полностью обесценятся. Задача отдела логистики — определить оптимальную партию закупки запасных частей Q*. При этом следует учитывать случайный спрос, который характеризуется тем, что вероятность выхода из строя m деталей равна Qa.3(m).
Поскольку спрос носит вероятностный характер, выразим математическое ожидание издержек H(Q), которые складываются из затрат на закупку запасных частей и потерь от дефицита в случае их нехватки:
![]()

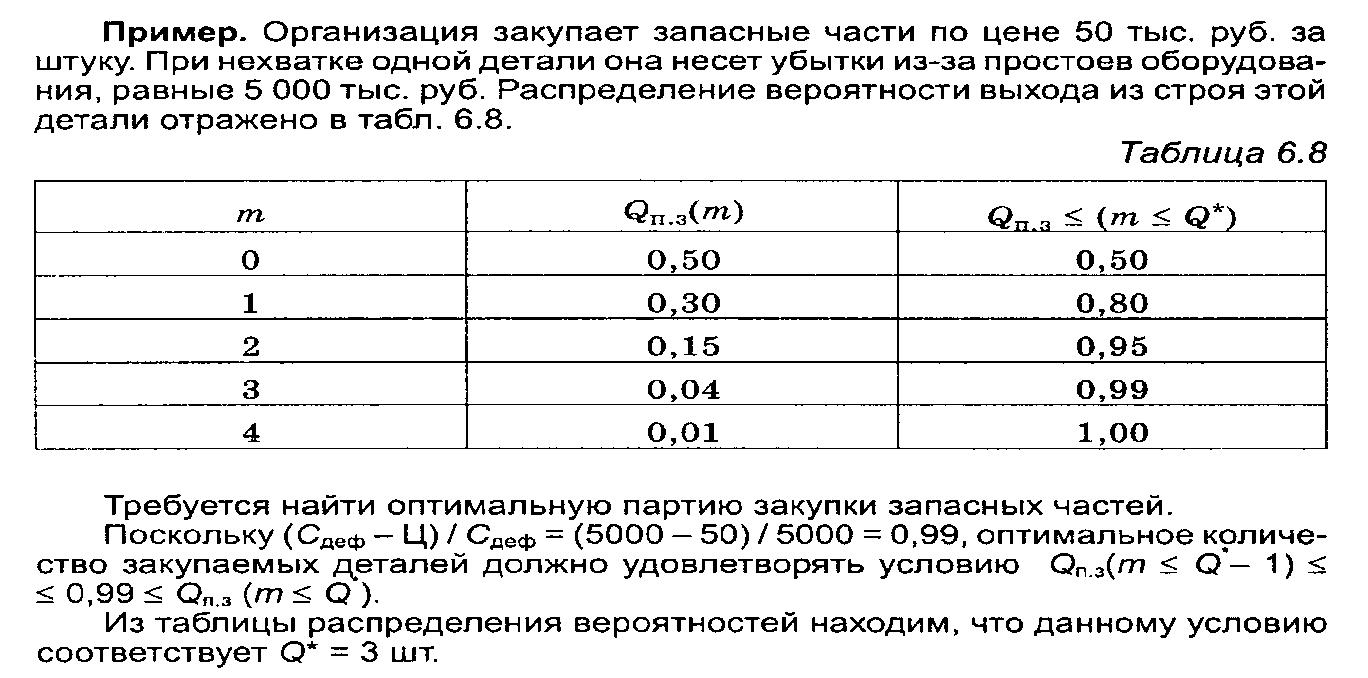
В рассмотренном случае созданные сверх потребности запасы продуктов полностью обесцениваются. Если при неиспользовании продукта возможна его реализация по цене Ц1<Ц (закупочной), выражение (6.32) преобразуется и оптимальная партия закупки рассчитывается из следующего неравенства:
![]()
В торговле часто приходится решать задачу оптимальной партии закупки товара и, соответственно, оптимального товарного запаса при случайном спросе с использованием в качестве критерия максимума прибыли (в исследованиях операций она называется «задачей о новогодней елке»).
Если организация закупает товар, спрос на который носит случайный характер, по цене Ц, а продает по цене Ц2, то нереализованная продукция полностью обесценивается. Величина прибыли от реализации составляет разницу между выручкой от реализации и суммой, затраченной на покупку товара, что выражается следующей целевой функцией прибыли:
![]()
В результате оптимизации целевой функции получаем выражение для вычисления партии закупки товара, обеспечивающей предприятию максимальную прибыль:
![]()
Общий вариант задачи управления запасами при случайном спросе представляет ситуация, когда организация несет потери от дефицита, а остатки товара реализуются по сниженной цене Ц1. Партия заказа, дающая максимальную прибыль, рассчитывается по формуле
![]()
