3.2. Напряженность электростатического поля двух

разноименно заряженных бесконечно протяженных плоскостей

Пусть две параллельные бесконечно протяженные плоскости заряжены равномерно с поверхностной плотностью заряда  =+  =  .

Результирующую напряженность электрического поля в этом случае можно найти, используя принцип суперпозиции полей, созданных каждой из заряженных плоскостей в отдельности (рис. 4), где линии напряженности с двумя стрелками соответствуют полю положительно заряженной плоскости, а с одной стрелкой  полю отрицательно заряженной плоскости. В соответствии с рис. 4 слева и справа от плоскостей электрическое поле равно нулю (Е ₊ = Е  = 0).

Между плоскостями линии напряженности направлены в одну сторону, следовательно, с учетом (13) имеем

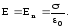(14)

Таким образом, электрическое поле между заряженными разноименно бесконечно протяженными плоскостями однородно, за исключением краевых эффектов. Если размеры плоскостей (пластин) много больше расстояния между ними, то полученный результат остается справедливым и для пластин конечных размеров (плоский конденсатор).

3.3. Поле равномерно заряженной сферической поверхности

Рис. 5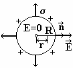

Пусть сферическая поверхность радиуса R заряжена равномерно с поверхностной плотностью заряда +. Электрическое поле заряженной сферы  центральносимметричное. Силовые линии напряженности направлены от поверхности на продолжение радиусов, а модуль вектора 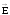должен зависеть только от расстояния r до поверхности сферы. В качестве замкнутой поверхности проще всего использовать концентрическую сферу радиуса r, проходящую через ту точку электрического поля, в которой требуется определить напряженность этого поля.

Рассмотрим три случая:

а) r  R.

Внутри сферы зарядов нет. Все заряды расположены на внешней поверхности сферы, т. е. в любой точке внутри сферы Е = 0 (рис. 5);

б) r  R (рис. 6).

В качестве замкнутой поверхности возьмем концентрическую сферу радиуса r . Найдем напряженность поля, например, в т. Б;

Поток вектора 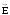, т. е. Ф_е = Е S_r (Е = Е_n, ),

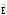
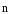где S_r = 4r²  площадь сферической поверхности радиуса r.

Рис. 6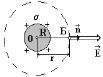

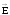
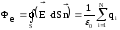Согласно теореме Гаусса поток вектора

,

или

где ;

Рис. 7

S_R = 4R²  площадь сферической поверхности радиуса

R. Таким образом, 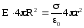Следовательно,

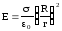. (15)

Если в формуле (15) поверхностную плотность заряда , заменить на заряд q,

т. е. 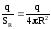, то .

Вывод: на любом расстоянии r от заряженной сферы напряженность электрического поля можно найти по формуле напряженности точечного заряда, если весь заряд сферы сосредоточить в ее центре (т. 0);

в) r = R. В этом случае нужно в формуле (15) вместо r запишем R, тогда

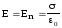
или .

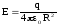График изменения напряженности электрического поля заряженной сферической поверхности от расстояния r приведен на рис. 7.

Уравнения Пуассона и Лапласа

Общая задача электростатики заключается в том, что если неизвестно распределение зарядов, но известны потенциалы проводников, их относительное расположение и форма, то можно определить потенциал в любой точке электростатического поля между проводниками. Зная потенциал , можно найти напряженность поля 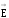, что даст возможность указать распределение поверхностных зарядов проводников.

Для нахождения дифференциального уравнения, которому удовлетворяет функция   потенциал, воспользуемся дифференциальной формой теоремы гаусса.

Решив совместно эти уравнения, получим общее дифференциальное уравнение Пуассона  уравнение для потенциала в виде

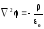, (2)

где ²  оператор Лапласа, который в декартовых координатах записывается в виде .

При отсутствии зарядов между проводниками уравнение Пуассона переходит в уравнение Лапласа, т. е. ² = 0. (3)

Уравнения Пуассона и Лапласа позволяют решить общую задачу электростатики, решение которой является единственным (теорема единственности).

15. электрический диполь. Энергия диполя.