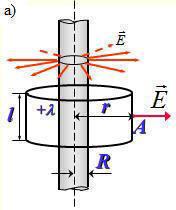
4. Поле равномерно заряженного бесконечного цилиндра (нити)

 

Рис. 1.13. Электрическое поле равномерно заряженного цилиндра

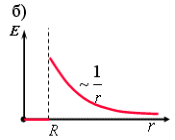
Бесконечный цилиндр радиуса R заряжен равномерно; линейная плотность заряда равна l. Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l (рис. 1.13 а). Поскольку вектор напряженности параллелен торцам, поток сквозь основания цилиндра равен нулю, и .   Отсюда при r  R .   Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0. График зависимости E от r приведен на рис. 1.13 б.

6. Работа сил электростатического поля в случае двух точечных зарядов. Потенциал. Потенциал поля, создаваемого системой точечных зарядов.

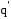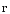Работа сил электростатического поля. Для точечных зарядов сила, действующая на заряд , направлена вдоль линии, соединяющей заряды q и , т.е. по радиус-вектору (заряд q находится в начале координат) (см. рис. 3.1).

Рис. 3.1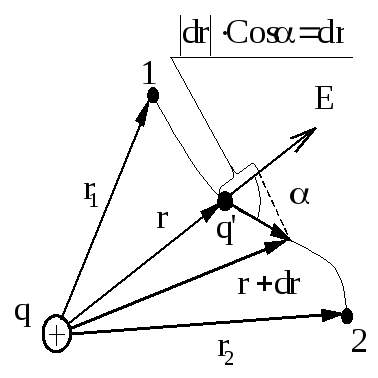

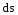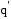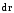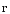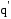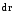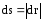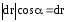Вектор бесконечно малого перемещения заряда совпадает, при таком выборе системы координат, с вектором – бесконечно малым приращением радиус-вектора заряда . Значит ds – модуль бесконечно малого перемещения – равен модулю вектора , ^{т. е.} . ^{Из рисунка видно, что} , ^{здесь dr} – бесконечно малое приращение длины вектора .

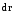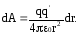
Работа на всем пути, от точки 1 до точки 2, равна:

^.

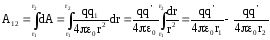Потенциал.

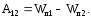
потенциальная энергия взаимодействия двух точечных зарядов в вакууме дается следующей формулой: 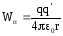^. (3.3)

Из формулы (3.3) видно, что потенциальную энергию взаимодействия двух точечных зарядов можно представить как произведение величины второго заряда 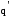на функцию , зависящую от величины первого заряда q и расстояния до точки, в которой находится второй заряд:

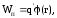где 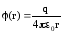– потенциал электростатического поля точечного заряда

В общем случае электростатический потенциал  поля, создаваемого произвольным распределением зарядов равен, по определению, отношению потенциальной энергии 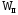пробного заряда 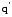в электростатическом поле к величине этого пробного заряда:

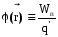^. (3.5)

Единица потенциала в системе СИ – вольт (В):

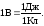
Зная 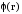– потенциал электростатического поля в любой точке пространства, легко найти потенциальную энергию 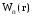любого точечного заряда q, помещенного в данную точку пространства:

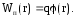(3.6)

Следовательно, работу электростатического поля по перемещению электрического заряда можно выразить, используя (3.2) и (3.6), следующим образом:

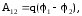(3.7)

здесь – потенциалы поля в точках, между которыми переместился заряд.

Потенциал поля, создаваемого системой точечных зарядов.

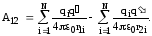
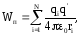
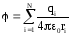
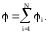- Формула выражает принцип суперпозиции для потенциала электростатического поля: потенциал поля системы зарядов равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.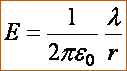