Свойства уравнений Максвелла:1. Уравнения Максвелла линейны.

2. Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения заряда. 3. Уравнения Максвелла выполняются во всех инерциальных системах отчета. 4. Уравнения Максвелла симметричны.

32. Электромагнитные волны. Поток энергии электромагнитного поля (Вектор Умова-Пойтинга).

Электромагнитные волны

Из уравнений Максвелла следует, что электромагнитное поле способно существовать самостоятельно, без электрических зарядов и токов. Изменяющееся электромагнитное поле имеет волновой характер и распространяется в вакууме в виде электромагнитных волн со скоростью света.

Существование электромагнитных волн вытекает из уравнений Максвелла, которые описываются волновыми уравнениями для векторов 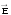и 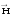соответственно:

Рис. 5.2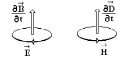

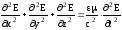, (5.18)

, (5.19)

Изменение во времени магнитного поля возбуждает переменное электрическое поле и, наоборот, изменение во времени электрического поля возбуждает переменное магнитное поле. Вихревое электрическое поле, индуцированное переменным магнитным полем 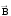, образует с вектором 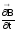левовинтовую систему (рис. 7.2), а вихревое магнитное поле, индуцированное электрическим полем 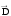, образует с вектором правовинтовую систему (рис. 5.2).

Происходит непрерывное их взаимопревращение, что и дает возможность

существовать и распространяться им в пространстве и времени при отсутствии зарядов и токов.

Таким образом, теория Максвелла не только предсказала существование электромагнитных волн, но и установила их важнейшие свойства:

1. Скорость распространения электромагнитной волны в нейтральной непроводящей и неферромагнитной среде

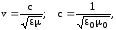(5.20)

где c  скорость света в вакууме.

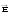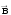2. Векторы , и 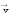взаимно перпендикулярны и образуют правовинтовую систему (рис.5.3). В этом проявляется внутреннее свойство электромагнитной волны, не зависящей ни от какой координатной системы.

Рис. 5.3 Рис. 5.4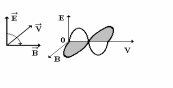

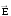3. В электромагнитной волне векторы и 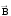всегда колеблются в одинаковых фазах (рис. 5.4), причем между мгновенными значениями Е и В в любой точке пространства

существует связь, а именно: Е = vB или 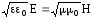. ( 5.21)

Существование электромагнитных волн позволило Максвеллу объяснить волновую природу света. Свет  это электромагнитные волны.

Поток энергии электромагнитного поля

При распространении электромагнитных волн в пространстве и времени они несут с собой энергию. Она заключена во взаимно превращающихся электрическом и магнитном полях.

Объемная плотность энергии электрического поля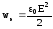, (5.22)

где Е  напряженность электрического поля.

Объемная плотность энергии магнит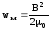ного поля , (5.23) где В  индукция магнитного поля.

Следовательно, объемная плотность энергии электромагнитного поля в той области пространства, где находится в произвольный момент времени электромагнитная волна,

W = w _э+ w_м = 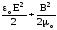. (5.24)

Или с учетом того, что Е = сВ и 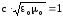, имеем w = _oE² , (5.25) или 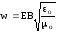. (5.26)

Энергию, переносимую электромагнитной волной в единицу времени через единичную площадку, называют плотностью потока электромагнитной энергии. Вектор плотности потока электромагнитной энергии называют вектором Пойнтинга.

Направление вектора Пойнтинга 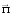совпадает с направлением распространения электромагнитной волны, т. е. с направлением переноса энергии. Скорость переноса энергии равна фазовой скорости этой волны.

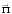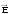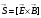Вектор Пойнтинга совпадает по направлению со скоростью распространения электромагнитной волны, которая перпендикулярна и , т. е. . (5.29)

Измеряется в Вт/м²