21,Работа, мощность, кпд источника тока. Тепловое действие тока. Закон Джоуля-Ленца.

Если по проводнику течет ток силой I, то за время dt через сечение проводника пройдет заряд:

Заряд, равный dq, в сечении 1 войдет в проводник и точно такой же заряд выйдет из проводника. Можно считать, что за время dt заряд сместился из сечения 1 в сечение 2, при этом над зарядом электростатическими силами совершена работа (см. (3.11)):

Мощность, развиваемая на участке цепи между точками 1 и 2, по определению равна:

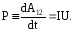
Заменяя, согласно закону Ома (6.5), напряжение U.

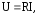
получаем формулы для количества тепла dQ и мощности P:

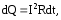Формулу называют законом Джоуля-Ленца.

Если измерять тепло в калориях, в формуле (7.3) появляется переводной коэффициент, равный значению 1 Дж в калориях – 0,24 (кал/Дж):

, (кал

Точно так же, как выводится закон Ома в дифференциальной форме, выводится закона Джоуля-Ленца в дифференциальной форме. Этот закон определяет количество тепла, выделяющееся в единичном объеме проводника в единицу времени – удельную тепловую мощность тока w:

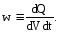
Рассмотрим однородный цилиндрический проводник. Подставим в формулу (7.4) из (6.6) и (6.2) значения: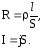

После подстановки получаем: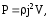 где

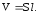
Из формулы (7.6) видно, что мощность, выделяемая в единице объема проводника, удельная тепловая мощность тока, равна: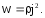 (7.7)

Для w, пользуясь законом Ома в дифференциальной форме (формула (6.10)), можно записать на основе (7.6) следующие эквивалентные выражения закона Джоуля-Ленца в дифференциальной форме: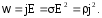 (7.8)

Для количества тепла dQ, выделяющегося в объеме dV за время dt, из (7.8) получаем:

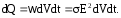(7.9)

В случае неоднородного проводника формулы (7.8) и (7.9) позволяют найти количество тепла, выделяемого в каждой точке объема неоднородного проводника.

Если участок цепи неоднородный, то выделяемое количество теплоты по закону сохранения энергии будет равно алгебраической сумме работ кулоновских и сторонних сил.

Действительно, умножив правую и левую части формулы на силу тока I получим

I²R = (₁  ₂)I + 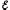₁₂I. (5.28)

Следовательно, из уравнения (5.28) следует, что тепловая мощность Q = I²R , (5.29)

выделяемая на участке цепи 1-2, равна алгебраической сумме мощностей кулоновских и сторонних сил. Если цепь замкнута, то затраченная мощность N =I 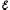. (5.30)

Если электрическая цепь замкнута и содержит источника с ЭДС 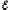, то вся затраченная источником тока работа А_З = А_П + А_ВНУТ,

где А_З = I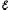t, А_П = IU_Rt, А_ВНУТ = IU_rt.

Тогда 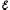= U_R + U_r = IR+ Ir, (5.20)

где U_R - напряжение на внешнем сопротивлении, U_r - напряжение на внутреннем сопротивлении источника тока.

Мощность тока можно найти по формуле N = 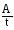. (5.21)

Развиваемая источником тока затраченная мощность N_З = N_П + N_ВНУТ где N_З= I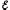, N_П = IU_R, N_ВНУТ = IU_r.

КПД источника тока можно найти по формуле 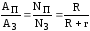 = . (5.23)

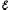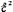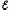Затраченная источником тока мощность N_З = I=/(R+r), где I = /(R + r).

Полезная мощность, выделяемая во внешнем участке цепи N_П = IU_R = I²R =.

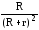
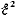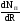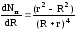
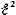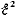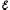
Следовательно, затраченная и полезная мощности являются функциями от внешнего сопротивления. Если R 0, то N_П  0; R , то N_П  0. В этом случае функция N_П = f₂ (R) имеет один максимум. Найдем условие, при котором полезная мощность максимальна, т. е. N_П = N_П, _МАХ. Для этого производную приравняем нулю, т. е. = 0, т. е. (r²-R²) = 0. (  0, то R = r и  = 0,5). Вывод: Если R = r , то полезная мощность максимальна, а КПД источника тока равно 50%.