Сила тока, плотность тока

Выше (см. лекцию 5) мы установили, что если проводник внести в электрическое поле, то под действием поля свободные заряды проводника смещаются – говорят, что возникают индуцированные заряды. Поле индуцированных зарядов компенсирует внешнее, напряженность электрического поля становится равной нулю и движение зарядов прекращается.

Предположим, что мы искусственно создали условия, при которых индуцированный заряд не формируется, например, мы с помощью тонких проводников (их называют проводами) отводим заряды с одной стороны от исследуемого проводника и подводим с другой (см. рис. 6.1).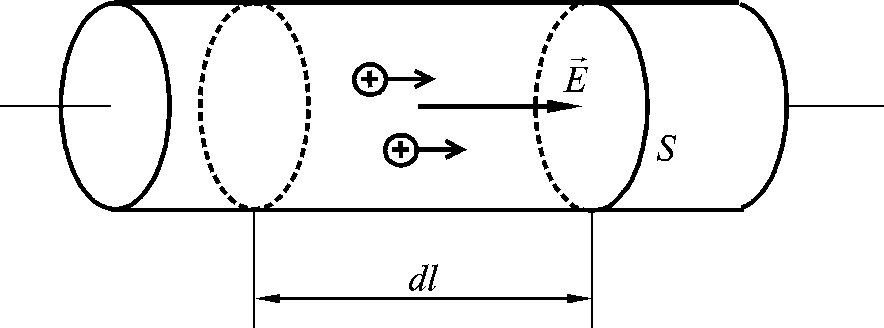

Рис. 6.1

В результате в проводнике присутствует электрическое поле и существует постоянное упорядоченное движение зарядов под действием электрического поля.

Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов.

Если направленное движение происходит под действием электрического поля, ток называют током проводимости, если упорядоченное движение – это движение зарядов под действием механического перемещения макроскопического тела, то ток называется конвекционным.

Количественной характеристикой электрического тока служит сила тока. Если через поперечное сечение проводника за время dt проходит заряд dq, то по определению сила тока: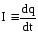^. (6.1)

Сила тока – скалярная величина, определяемая электрическим зарядом, проходящим через поперечное сечение в единицу времени. За направление тока условно принимается направление перемещения положительных зарядов.

Единица силы тока – «ампер» (А); единицы силы тока и заряда связаны соотношением: 1 Кл = 1 А·с.

Если сила тока и его направление не меняются во времени, то такой ток называют постоянным, если меняется, то ток называют переменным.

Плотность тока

Ток может протекать через проводник большого сечения, при этом величина заряда, переносимого через отдельные участки сечения, может меняться. Более того, может меняться и направление движения зарядов (см. рис. 6.2).

В связи с этим вводится понятие плотности тока.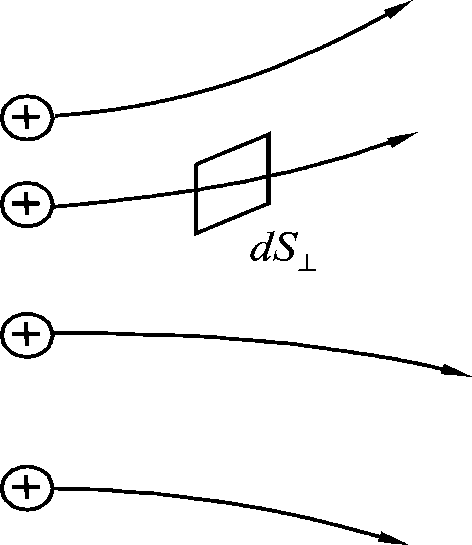

Выделим в проводнике площадку 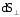, перпендикулярную направлению движения зарядов в этой точке проводника. Пусть сила тока, протекающего через эту площадку равна . Плотность тока по определению равна:

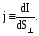(6.2)

Если известен вектор плотности тока в каждой точке некоторой поверхности S, то можно найти силу тока через эту поверхность как поток вектора плотности тока, т. е. ,

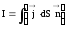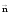
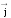где  единичный вектор нормали к поверхности. За направление вектора принято направление упорядоченного движения положительных зарядов.

Графически поле вектора плотности тока изображают с помощью линий тока. Там, где линии тока проведены гуще, плотность тока больше.

Плотность тока характеризуется не только своей величиной j, но и направлением движения зарядов. Следовательно, плотность тока – вектор, формула (6.2) определяет его модуль.

Плотность тока – это векторная физическая величина, модуль которой равен силе тока через единичную площадку, перпендикулярную направлению движения зарядов в данной точке проводника, а направление совпадает с направлением движения зарядов.

Из формулы (6.2) следует, что единица измерения плотности тока:

Графически движение зарядов в проводнике может быть представлено с помощью линий вектора плотности тока.

19.Уравнение непрерывности. Закон Ома для однородного участка проводника.