
- •Оглавление
- •Введение
- •Глава 1. МИКРОПРОЦЕССОРНЫЕ СИСТЕМЫ
- •1.1. Понятие архитектуры вычислительной системы. Структура аппаратной части и назначение основных функциональных узлов
- •1.2. Базовые параметры и технические характеристики ЭВМ
- •Контрольные вопросы к главе 1
- •Глава 2. СТРУКТУРА И ФУНКЦИОНИРОВАНИЕ ПРОЦЕССОРА
- •2.2. Устройство управления с программируемой логикой
- •2.3. Устройство управления с жесткой логикой
- •2.4. Слово состояния процессора
- •2.5. Микроконтроллеры
- •2.6. Особенности организации однокристальных и секционных микропроцессоров
- •2.8. Архитектура и функционирование микропроцессора
- •Контрольные вопросы к главе 2
- •Глава 3. СИСТЕМЫ КОМАНД МИКРОЭВМ
- •3.1. Язык микроопераций для описания вычислительных устройств
- •3.2. Структура и формат команд микропроцессора и МПС
- •3.3. Программирование микропроцессора
- •Контрольные вопросы к главе 3
- •Глава 4. ТЕНДЕНЦИИ РАЗВИТИЯ АРХИТЕКТУРЫ И АППАРАТНОГО ОБЕСПЕЧЕНИЯ ЭВС
- •4.1. Требования различных задач к вычислительным ресурсам и ограничения фон-Неймановской архитектуры
- •4.2. Распараллеливание процессов обработки информации
- •4.3. Принцип совмещения операций. Конвейерная обработка информации
- •4.4. Архитектура процессоров с сокращенным набором команд
- •4.5. Применение кэш-памяти и повышение пропускной способности
- •4.6. Транспьютеры
- •4.7. Развитие новых архитектурных принципов
- •4.8. Оценка производительности скалярного процессора
- •Контрольные вопросы к главе 4
- •Глава 5. ОПЕРАТИВНАЯ ПАМЯТЬ
- •5.1. Классификация и иерархическая структура памяти ЭВМ
- •5.2. Запоминающие элементы статических ОЗУ
- •5.3. Запоминающие элементы динамических ОЗУ
- •5.4. Структуры матриц накопителей информации
- •5.5. Структура построения БИС статических ОЗУ и модулей памяти
- •5.6. Структура построения БИС динамических ОЗУ
- •5.7. Элементная база и организация постоянных запоминающих устройств
- •Контрольные вопросы к главе 5
- •Глава 6. ВНЕШНИЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА НА МАГНИТНЫХ НОСИТЕЛЯХ
- •6.1. Принцип записи двоичной информации на магнитную поверхность
- •6.3. Методы записи цифровой информации на магнитный носитель
- •6.4. Воспроизведение информации и повышение ее достоверности
- •6.5. Накопители на гибких магнитных дисках и их контроллеры
- •6.6. Накопители на жестких магнитных дисках типа винчестер и их контроллеры
- •6.7. Накопители на сменных магнитных дисках
- •6.8. Накопители на магнитной ленте
- •Контрольные вопросы к главе 6
- •Глава 7. ОПТИЧЕСКИЕ И МАГНИТООПТИЧЕСКИЕ ВЗУ
- •7.1. Лазерные системы и их применение в устройствах внешней памяти
- •7.2. Оптические диски
- •7.3. Магнитооптические диски
- •7.4.Устройство накопителя на оптических дисках
- •Контрольные вопросы к главе 7
- •Глава 8. ВЗУ НА ЦМД-СОДЕРЖАЩИХ МАТЕРИАЛАХ
- •8.1. Принципы возникновения цилиндрических магнитных доменов
- •8.2. Организация продвижения ЦМД
- •8.4. Структура ЦМД-микросхем памяти
- •8.5. Устройство ЦМД-накопителя
- •Контрольные вопросы к главе 8
- •Глава 9. ВЗУ НА ОСНОВЕ ГОЛОГРАФИИ
- •9.1. Носители информации голографических ЗУ
- •9.2. Создание голограмм
- •9.3. Воспроизведение голограмм
- •9.4. Голографические ЗУ двоичной информации
- •Контрольные вопросы к главе 9
- •Глава 10. ОРГАНИЗАЦИЯ БЕЗАДРЕСНОЙ И ВИРТУАЛЬНОЙ ПАМЯТИ
- •10.1. Стековая память
- •10.2. Ассоциативная память
- •10.3. Виртуальная память со страничной организацией
- •10.4. Структура виртуальной памяти при сегментном распределении
- •Контрольные вопросы к главе 10
- •Глава 11. НАЗНАЧЕНИЕ ПЕРИФЕРИЙНЫХ УСТРОЙСТВ
- •11.1. Классификация периферийных устройств
- •Контрольные вопросы к главе 11
- •Глава 12. УСТРОЙСТВА АВТОМАТИЧЕСКОГО СЧИТЫВАНИЯ ТЕКСТОВ
- •12.1. Устройства автоматического ввода печатных текстов
- •12.2. Методы распознавания образов печатных знаков
- •12.3. Устройства автоматического ввода рукописных текстов
- •12.4. Средства считывания и хранения графических изображений поврежденных рукописных текстов
- •12.5. Кодирование текстов для электронных публикаций
- •Контрольные вопросы к главе 12
- •Глава 13. УСТРОЙСТВА АВТОМАТИЧЕСКОГО ВВОДА ИЗОБРАЖЕНИЙ
- •13.1. Устройства автоматического ввода одноконтурных изображений
- •13.2. Устройства автоматического ввода многоконтурных и полутоновых изображений
- •13.3. Считывание цветных изображений
- •Контрольные вопросы к главе 13
- •Глава 14. УСТРОЙСТВА ПОЛУАВТОМАТИЧЕСКОГО ВВОДА ГРАФИЧЕСКОЙ ИНФОРМАЦИИ - ДИГИТАЙЗЕРЫ
- •14.1. Устройство рабочего поля планшета
- •14.2. Структурная схема дигитайзера и ее функционирование
- •Контрольные вопросы к главе 14
- •Глава 15. УСТРОЙСТВА ВВОДА - ВЫВОДА РЕЧЕВОЙ ИНФОРМАЦИИ
- •15.1. Модель речи
- •15.2. Структурная схема анализатора речи
- •15.3. Структура устройств ввода речи
- •15.4.Устройства вывода речевой информации - синтезаторы
- •Контрольные вопросы к главе 15
- •Глава 16. УСТРОЙСТВА ОТОБРАЖЕНИЯ ИНФОРМАЦИИ - ДИСПЛЕИ
- •16.1. Классификация дисплеев
- •16.2. Способы формирования изображения на экране телевизионного дисплея
- •16.3. Структурная схема текстового телевизионного дисплея
- •16.4. Структурная схема графического телевизионного дисплея
- •16.5. Устройство плоских экранов
- •Контрольные вопросы к главе 16
- •Глава 17. АВТОМАТИЧЕКИЕ УСТРОЙСТВА РЕГИСТРАЦИИ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ - ГРАФОПОСТРОИТЕЛИ
- •17.1. Классификация и устройство графопостроителей
- •17.2. Принципы работы графопостроителя по вычерчиванию
- •17.3. Структурная схема планшетного графопостроителя
- •17.4. Структурная схема растрового графопостроителя
- •Контрольные вопросы к главе 17
- •Глава 18. АППАРАТУРА ПРИЕМА-ПЕРЕДАЧИ ИНФОРМАЦИИ
- •18.1. Обобщенная структурная схема аппаратуры передачи дискретной информации
- •18.2. Характеристики аппаратуры передачи данных
- •18.3. Принципы организации интерфейсов
- •18.4. Классификация интерфейсов
- •Контрольные вопросы к главе 18
- •Глава 19. АВТОМАТИЧЕСКИЕ УСТРОЙСТВА ВВОДА-ВЫВОДА АНАЛОГОВОЙ ИНФОРМАЦИИ В ЭВМ
- •19.1. Назначение устройств ввода-вывода аналоговой информации в ЭВМ
- •19.2. Принципы построения ЦАП и АЦП
- •19.3. Принципы построения и программирование системы ввода-вывода аналоговой информации в ЭВМ
- •Контрольные вопросы к главе 19
- •Глава 20. КАНАЛЫ ВВОДА-ВЫВОДА И АППАРАТУРА СОПРЯЖЕНИЯ
- •20.2. Организация обмена массивами данных
- •20.3. Мультиплексный канал
- •20.4. Селекторный канал
- •20.5. Устройства сопряжения - мультиплексоры передачи данных
- •Контрольные вопросы к главе 20
- •Глава 21. УСТРОЙСТВА ЗАЩИТЫ ОТ ОШИБОК В ПЕРЕДАВАЕМОЙ ИНФОРМАЦИИ
- •21.1. Причины возникновения ошибок в передаваемой информации
- •21.2. Краткая характеристика способов защиты от ошибок
- •21.3.Обнаруживающие коды - с проверкой на четность и итеративный код
- •21.4. Корректирующий код Хэмминга
- •21.5. Циклические коды
- •21.6. Циклический код Файра как средство коррекции пакетов ошибок
- •Контрольные вопросы к главе 21
- •ЗАКЛЮЧЕНИЕ
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Приложение 7
- •Приложение 8
- •Приложение 9
- •Приложение 10
- •Приложение 11
- •Приложение 12
- •Приложение 13
- •Приложение 14
- •Приложение 15
- •Приложение 16
- •Приложение 17
- •Приложение 18
- •Приложение 19
- •Приложение 20
- •Приложение 22
- •Приложение 23
- •Приложение 24
- •Приложение 25
- •Приложение 26
- •Предметный указатель
- •Список литературы
Глава 21. Устройства защиты от ошибок в передаваемой информации |
298 |
Пример 21.2. Пусть имеется информационное слово А=1011. Согласно формуле
2r - r - 1≥ k,
необходимо сформировать 3 контрольных разряда, которые в кодовом слове займут 1, 2 и 4 позиции, а именно:
7 |
6 |
5 |
4 |
3 |
2 |
1 |
а4 а3 а2 r3 а1 r2 |
r1 |
|||||
Сформируем по модулю 2 контрольные разряды в соответствии с таблицей 21.2: r1=а1+а2+а4=1+1+1=1
r2=а1+а3+а4=1+0+1=0 r3=а2+а3+а4=1+0+1=0.
Получаем итоговое слово 1010101.
Можно построить КХ с d=4, который позволит корректировать одну и обнаруживать две ошибки. Для этого вводится еще один контрольный разряд для проверки на четность общего количества единиц в слове. Принятие решения об исправлении ошибки производится в соответствии с таблицей 21.3.
Таблица 21.3. Код Хэмминга с обнаружением двух и исправлением одной ошибки
______________________________________________________________
Проверочные Разряд Наличие ошибок суммы четности
______________________________________________________________
Нули |
0 |
нет ошибок |
>0 |
1 |
одиночная ошибка |
>0 |
0 |
двойная ошибка |
Нули |
1 |
ошибка в контрольном разряде |
|
|
общей четности |
______________________________________________________________
21.5. Циклические коды
Циклические коды находят наибольшее распространение в СПД с обратной связью, что обусловлено их высокими корректирующими свойствами, сравнительно простой реализацией, невысокой избыточностью. Особенно они эффективны при обнаружении пакетных ошибок. Основное свойство циклических кодов, определившее их название, состоит в том, что любое n-разрядное кодовое слово
А=аn-1аn-2 . . . а1а0,
будучи циклически сдвинуто на один разряд, создает новое слово
А1=аn-2an-3 . . . a1a0an-1 ,
принадлежащее этому же циклическому коду.
Циклические коды относятся к блочным систематическим кодам, в которых каждая комбинация кодируется самостоятельно в виде блока таким образом, что информационные k и проверочные r элементы всегда находятся на определенных местах. Для упрощения процедуры кодирования и декодирования проверочные биты размещают в конце блока. Кодирование передаваемого сообщения осуществляется умножением двоичной последовательности G(х) на одночлен хr , имеющий ту же степень, что и образующий полином Р(х), с добавлением к этому произведению остатка R(х), полученного после деления произведения G(x)xr на образующий полином, то есть предаваемое в канал связи сообщение F(x) имеет вид:
F(x)=G(x)xr+R(x).
При декодировании принимаемая последовательность F(x) делится на образующий полином Р(х). Полученный нулевой остаток R(x)=0 свидетельствует об отсутствии ошибок в принятом блоке, а отличие от нуля - о наличии ошибок. Анализируя остаток, можно опре-
Глава 21. Устройства защиты от ошибок в передаваемой информации |
299 |
делить номера искаженных разрядов и скорректировать их.
Для построения циклических кодов в качестве образующих полиномов используются неприводимые многочлены. (Неприводимые многочлены делятся без остатка только на себя и на единицу). Р(х) может быть представлен в алгебраической форме либо в виде двоичного или восьмеричного числа. В последнем случае каждая восмеричная цифра отображает три разряда. Например, для полинома
Р(х)=х5+х3+1 двоичная запись имеет вид 101001, а соответствующая ему восьмеричная - 51. В табл. 21.4
приведены выборочно неприводимые многочлены до 12-й степени включительно. Полиномы записаны в алгебраической форме и в виде восьмеричных чисел (для степеней r≥ 6 - только восьмеричными числами).
Таблица 21.4. Неприводимые многочлены
__________________________________________________________
r Р(х) r P(x)
__________________________________________________________
2 |
х2+х+1 |
7 |
7 |
211, 217, 235 |
3 |
х3+х+1 |
13 |
8 |
747, 435, 543 |
4 |
х4+х+1 |
23 |
9 |
1055, 1751 |
5 |
х5+х2+1 |
45 |
10 |
2033, 3177 |
6 |
х5+х4+х3+х2+х |
75 |
11 |
7413, 4505 |
|
|
|
12 |
15647, 11015 |
__________________________________________________________
При выборе полинома следует иметь в виду, что степень образующего полинома не может быть меньше числа проверочных элементов r.
Одним из множеств разновидностей циклических кодов наиболее широко используются для исправления и обнаружения пакетов ошибок коды с кодовым расстоянием d≥ 5, разработанные Боузом, Чоудхури и Хоквингемом (БЧХ-коды). Коды БЧХ обнаруживают и исправляют любое число ошибок. При кодировании заданными являются число tи ошибок, которые нужно исправить, и длина блока n. Необходимо определить число информационных k и проверочных r элементов, а также вид образующего полинома.
Длина кодовой комбинации определяется по формуле n=2m-1,
где m - целое число. Например, при m=6 n=63; при m=7 n=127; при m=8 n=255 и т.д. Образующий полином находится как наименьшее общее кратное (НОК) минималь-
ных нечетных полиномов mi(x) до порядка 2tи-1 включительно:
Р(х)=НОК{m1(x)m3(x) . . . m2tn-1(x)}.
Минимальный многочлен представляет собой простой неприводимый полином. Существуют многочлены одного и того же порядка различных степеней. Степень минимальных многочленов, входящих в данное уравнение, должна быть равной m. Так как порядок (номер) самого старшего минимального многочлена 2tи-1, то количество многочленов, входящих в выражение для Р(х), равно числу исправляемых ошибок tи. Например, если tи=5, то 2tи-1=9 и в выражение для Р(х) будут входить многочлены m1(x), m3(x), m5(x), m7(x), m9(x).
Минимальные многочлены циклических кодов различных степеней представлены в приложении, где значения mI(x) даны в восьмеричной системе счисления. Так, полином 13-го порядка 9-й степени, представленный числом 453, в двоичной форме имеет вид 100101011, а многочлен записывается как х8+х5+х3+х+1. Для нахождения Р(х) необходимо выписать из таблицы все значения минимальных полиномов, соответствующих степени m, до порядка 2tи-1 включительно. При отсутствии в таблице полинома нужного порядка можно взять ближайший меньший, а если среди минимальных многочленов окажутся два одинаковых, то выбирают один из них.
Глава 21. Устройства защиты от ошибок в передаваемой информации |
300 |
Пример 21.3. Рассчитать параметры кода для симплексного УЗО, позволяющего исправлять четырехкратные ошибки.
Кодовое расстояние, позволяющее исправлять четырехкратные ошибки, вычисляем по формуле d=tо+tи+1=2tи+1=2·4+1=9. Так как d>5, то для исправления ошибок следует применить код БЧХ с d=9. Для выполнения условия n=2m-1 длину блока информации будем выбирать из ряда 127, 255, 511, 1023 и т.д. Пусть n=511, тогда по формуле n=2m-1 m=9, а r<=9· 4=36. Количество информационных бит в блоке k=475. Так как длина информационной части блока должна быть кратна байту, то число знаков в блоке kзн=475/8=59.Тогда длина информационной части k= 59· 8=472. Оставшиеся свободными три бита могут быть использованы для передачи, например, номера блока.
Количество минимальных многочленов образующего полинома равно tи=4, порядок последнего полинома 2tи-1=7, старшая степень m=9. Из таблицы приложения выписываем минимальные многочлены требуемой степени получаем вид образующего полинома:
P(x)=(x9+x4+1)(x9+x6+x4+x3+1)(x9+x8+x5+x4+1)(x9+x7+x4+x3+1).
Число контрольных элементов полученного БЧХкода определяется степенью полученного образующего полинома и равно 36.
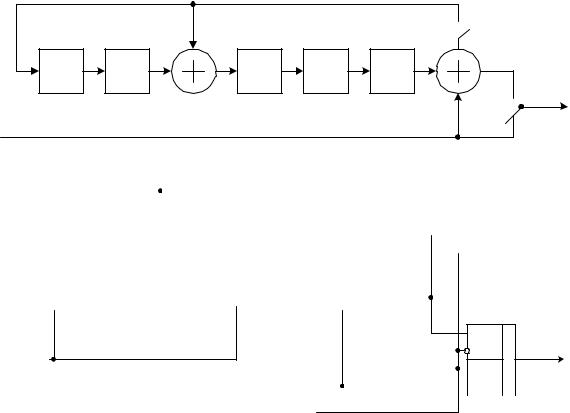
Для построения кодирующего устройства циклического кода необходимо выполнить две операции: умножить многочлен Q(x) на хr и полученное произведение разделить на образующий полином Р(х). Для выполнения первой операции не требуется специального устройства, так как умножение многочлена на хr означает добавление к нему r нулей со стороны младшего разряда, то есть после передачи k информационных элементов за ними следуют r проверочных. В качестве делителей полинома на полином в кодерах циклических кодов применяются устройства, построенные на основе регистров сдвига с обратными связями и сумматоров по модулю 2, причем схема делителя определяется видом образующего полинома. Количество триггеров регистра сдвига равно r. Число сумматоров - на единицу меньше количества ненулевых членов выражения Р(х). Сумматоры располагают перед ячейками регистра, соответствующими ненулевым членам образующего полинома. На рис. 21.7 приведена схема корректирующего устройства циклического кода с образующим полиномом х5+х2+1. Прямоугольниками обозначены ячейки памяти, кружками - сумматоры по модулю2. В исходном состоянии ключ К1 замкнут, а К2 находится в положении 2. Подлежащая кодированию комбинация поступает одновременно на вход кодера и через сумматор - на схему деления на Р(х). Деление начинается с приходом первого информационного элемента и оканчивается после выдачи в дискретный канал k-го бита. После этого схема управления УЗО переводит Л2 в положение 1, размыкает К1 и в течение последующих r тактов осуществляется выдача в УПС остатка от деления R(x), который был зафиксирован триггерами делителя. Функциональная
схема кодера на рис. 21.8 соответствует приведенной на рис. 21.7.
|
|
|
|
K1 |
|
|
|
|
X5 |
X0 |
X1 |
X2 |
X3 |
X4 |
|
|
|
|
На УПС |
Вход |
|
|
|
K2 |
Рис. 21.7. Структурная схема кодирующего устройства циклического кода
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RG |
|
|
|
|
|
|
|
|
RG |
|
|
|
|
|
|
|
|
& |
|
||
|
D 0 |
|
Q0 |
|
|
|
|
|
|
D 0 |
|
Q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Q3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
C |
|
Q1 |
|
|
|
|
|
|
C |
|
Q4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
& 1
Выход
ТИ |
|
|
|
|
& |
Вход |
|
||||
|
|
|
|||
|
|
|
|
|
|
|
От УУ |
|
|
||
|
|
|
|||
Рис. 21.8. Функциональная схема кодера циклического кода

Глава 21. Устройства защиты от ошибок в передаваемой информации |
301 |
От УПС
Буферный регистр
Дели- |
Деши- |
Выход |
|
тель |
Кл |
||
фратор |
|||
на |
к приёмнику |
||
ошибки |
сообщения |
||
Р(х) |
|||
|
|
От распределителя
Рис. 21.9. Структурная схема декодера циклического кода
Основу декодирующих устройств циклических кодов также составляют делители многочленов на образующий полином (рис 21.9). Признаком наличия ошибок в принятой последовательности является ненулевой остаток от деления ее на Р(х). До завершения процесса деления необходимо запоминать поступивший блок в буферном накопителе. После окончания цикла производится опрос делителя, и в случае ошибки принятый блок стирают. При нулевом остатке блок выводится получателю через ключ Кл, а на его место записывается следующий. Для исправления ошибок в приемной части УЗО сначала находят ошибочные разряды, а затем изменяют их значение, то есть инвертируют Рассмотрим на конкретном примере исправление двукратных ошибок.
Пример 21.4. На вход приемной части УЗО поступают комбинации циклического кода 15,7, получаемые с помощью образующего полинома Р(х)=х8+х7+х6+х4+1. В процессе воздействия помех 2 бита кодовой комбинации могут быть искажены. Необходимо обнаружить наличие ошибок в поступившей 15-разрядной последовательности и произвести их исправление.
Пусть в дискретный канал передана комбинация 100000011101000, которая на выходе приемной части УПС приняла вид 111000011101000. Разделим принятую последовательность на образующий полином Р(х)=111010001, в остатке получим R(x)=01001110, т.е. вес остатка W=4, что свидетельствует о наличии ошибки в принятой кодовой комбинации. Сдвигая циклически эту комбинацию влево на 1 бит, получаем 110000111010001. Разделим полученную последовательность снова на Р(х). Остаток от деления равен 10011100, т.е. W=4. Сдвигаем циклически комбинацию еще раз, после чего она принимает вид 100001110100011. Разделив ее на 111010001, получим остаток 11101001, вес которого W=5. После третьего сдвига и деления на образующий полином вес остатка 00000011 становится равным двум. Так как W<=tи=2, то складываем кодовую комбинацию, полученную в результате последнего сдвига с остатком: 0000111011000111+ +00000011=000011101000100. Произведя циклический сдвиг полученной суммы вправо, имеем исправленную последовательность 100000011101000, совпадающую с переданной в канал связи.
Функциональная схема декодера, реализующего рассмотренный в примере алгоритм, приведена в Приложении.
21.6. Циклический код Файра как средство коррекции пакетов ошибок
Из циклических кодов, обнаруживающих и исправляющих пакеты ошибок, наиболее эффективным является циклический код Файра (КФ), образующий полином которого Р(х) определяется выражением:
Рф(х)=Р(х)(хс+1),
