
- •Оглавление
- •Введение
- •Глава 1. МИКРОПРОЦЕССОРНЫЕ СИСТЕМЫ
- •1.1. Понятие архитектуры вычислительной системы. Структура аппаратной части и назначение основных функциональных узлов
- •1.2. Базовые параметры и технические характеристики ЭВМ
- •Контрольные вопросы к главе 1
- •Глава 2. СТРУКТУРА И ФУНКЦИОНИРОВАНИЕ ПРОЦЕССОРА
- •2.2. Устройство управления с программируемой логикой
- •2.3. Устройство управления с жесткой логикой
- •2.4. Слово состояния процессора
- •2.5. Микроконтроллеры
- •2.6. Особенности организации однокристальных и секционных микропроцессоров
- •2.8. Архитектура и функционирование микропроцессора
- •Контрольные вопросы к главе 2
- •Глава 3. СИСТЕМЫ КОМАНД МИКРОЭВМ
- •3.1. Язык микроопераций для описания вычислительных устройств
- •3.2. Структура и формат команд микропроцессора и МПС
- •3.3. Программирование микропроцессора
- •Контрольные вопросы к главе 3
- •Глава 4. ТЕНДЕНЦИИ РАЗВИТИЯ АРХИТЕКТУРЫ И АППАРАТНОГО ОБЕСПЕЧЕНИЯ ЭВС
- •4.1. Требования различных задач к вычислительным ресурсам и ограничения фон-Неймановской архитектуры
- •4.2. Распараллеливание процессов обработки информации
- •4.3. Принцип совмещения операций. Конвейерная обработка информации
- •4.4. Архитектура процессоров с сокращенным набором команд
- •4.5. Применение кэш-памяти и повышение пропускной способности
- •4.6. Транспьютеры
- •4.7. Развитие новых архитектурных принципов
- •4.8. Оценка производительности скалярного процессора
- •Контрольные вопросы к главе 4
- •Глава 5. ОПЕРАТИВНАЯ ПАМЯТЬ
- •5.1. Классификация и иерархическая структура памяти ЭВМ
- •5.2. Запоминающие элементы статических ОЗУ
- •5.3. Запоминающие элементы динамических ОЗУ
- •5.4. Структуры матриц накопителей информации
- •5.5. Структура построения БИС статических ОЗУ и модулей памяти
- •5.6. Структура построения БИС динамических ОЗУ
- •5.7. Элементная база и организация постоянных запоминающих устройств
- •Контрольные вопросы к главе 5
- •Глава 6. ВНЕШНИЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА НА МАГНИТНЫХ НОСИТЕЛЯХ
- •6.1. Принцип записи двоичной информации на магнитную поверхность
- •6.3. Методы записи цифровой информации на магнитный носитель
- •6.4. Воспроизведение информации и повышение ее достоверности
- •6.5. Накопители на гибких магнитных дисках и их контроллеры
- •6.6. Накопители на жестких магнитных дисках типа винчестер и их контроллеры
- •6.7. Накопители на сменных магнитных дисках
- •6.8. Накопители на магнитной ленте
- •Контрольные вопросы к главе 6
- •Глава 7. ОПТИЧЕСКИЕ И МАГНИТООПТИЧЕСКИЕ ВЗУ
- •7.1. Лазерные системы и их применение в устройствах внешней памяти
- •7.2. Оптические диски
- •7.3. Магнитооптические диски
- •7.4.Устройство накопителя на оптических дисках
- •Контрольные вопросы к главе 7
- •Глава 8. ВЗУ НА ЦМД-СОДЕРЖАЩИХ МАТЕРИАЛАХ
- •8.1. Принципы возникновения цилиндрических магнитных доменов
- •8.2. Организация продвижения ЦМД
- •8.4. Структура ЦМД-микросхем памяти
- •8.5. Устройство ЦМД-накопителя
- •Контрольные вопросы к главе 8
- •Глава 9. ВЗУ НА ОСНОВЕ ГОЛОГРАФИИ
- •9.1. Носители информации голографических ЗУ
- •9.2. Создание голограмм
- •9.3. Воспроизведение голограмм
- •9.4. Голографические ЗУ двоичной информации
- •Контрольные вопросы к главе 9
- •Глава 10. ОРГАНИЗАЦИЯ БЕЗАДРЕСНОЙ И ВИРТУАЛЬНОЙ ПАМЯТИ
- •10.1. Стековая память
- •10.2. Ассоциативная память
- •10.3. Виртуальная память со страничной организацией
- •10.4. Структура виртуальной памяти при сегментном распределении
- •Контрольные вопросы к главе 10
- •Глава 11. НАЗНАЧЕНИЕ ПЕРИФЕРИЙНЫХ УСТРОЙСТВ
- •11.1. Классификация периферийных устройств
- •Контрольные вопросы к главе 11
- •Глава 12. УСТРОЙСТВА АВТОМАТИЧЕСКОГО СЧИТЫВАНИЯ ТЕКСТОВ
- •12.1. Устройства автоматического ввода печатных текстов
- •12.2. Методы распознавания образов печатных знаков
- •12.3. Устройства автоматического ввода рукописных текстов
- •12.4. Средства считывания и хранения графических изображений поврежденных рукописных текстов
- •12.5. Кодирование текстов для электронных публикаций
- •Контрольные вопросы к главе 12
- •Глава 13. УСТРОЙСТВА АВТОМАТИЧЕСКОГО ВВОДА ИЗОБРАЖЕНИЙ
- •13.1. Устройства автоматического ввода одноконтурных изображений
- •13.2. Устройства автоматического ввода многоконтурных и полутоновых изображений
- •13.3. Считывание цветных изображений
- •Контрольные вопросы к главе 13
- •Глава 14. УСТРОЙСТВА ПОЛУАВТОМАТИЧЕСКОГО ВВОДА ГРАФИЧЕСКОЙ ИНФОРМАЦИИ - ДИГИТАЙЗЕРЫ
- •14.1. Устройство рабочего поля планшета
- •14.2. Структурная схема дигитайзера и ее функционирование
- •Контрольные вопросы к главе 14
- •Глава 15. УСТРОЙСТВА ВВОДА - ВЫВОДА РЕЧЕВОЙ ИНФОРМАЦИИ
- •15.1. Модель речи
- •15.2. Структурная схема анализатора речи
- •15.3. Структура устройств ввода речи
- •15.4.Устройства вывода речевой информации - синтезаторы
- •Контрольные вопросы к главе 15
- •Глава 16. УСТРОЙСТВА ОТОБРАЖЕНИЯ ИНФОРМАЦИИ - ДИСПЛЕИ
- •16.1. Классификация дисплеев
- •16.2. Способы формирования изображения на экране телевизионного дисплея
- •16.3. Структурная схема текстового телевизионного дисплея
- •16.4. Структурная схема графического телевизионного дисплея
- •16.5. Устройство плоских экранов
- •Контрольные вопросы к главе 16
- •Глава 17. АВТОМАТИЧЕКИЕ УСТРОЙСТВА РЕГИСТРАЦИИ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ - ГРАФОПОСТРОИТЕЛИ
- •17.1. Классификация и устройство графопостроителей
- •17.2. Принципы работы графопостроителя по вычерчиванию
- •17.3. Структурная схема планшетного графопостроителя
- •17.4. Структурная схема растрового графопостроителя
- •Контрольные вопросы к главе 17
- •Глава 18. АППАРАТУРА ПРИЕМА-ПЕРЕДАЧИ ИНФОРМАЦИИ
- •18.1. Обобщенная структурная схема аппаратуры передачи дискретной информации
- •18.2. Характеристики аппаратуры передачи данных
- •18.3. Принципы организации интерфейсов
- •18.4. Классификация интерфейсов
- •Контрольные вопросы к главе 18
- •Глава 19. АВТОМАТИЧЕСКИЕ УСТРОЙСТВА ВВОДА-ВЫВОДА АНАЛОГОВОЙ ИНФОРМАЦИИ В ЭВМ
- •19.1. Назначение устройств ввода-вывода аналоговой информации в ЭВМ
- •19.2. Принципы построения ЦАП и АЦП
- •19.3. Принципы построения и программирование системы ввода-вывода аналоговой информации в ЭВМ
- •Контрольные вопросы к главе 19
- •Глава 20. КАНАЛЫ ВВОДА-ВЫВОДА И АППАРАТУРА СОПРЯЖЕНИЯ
- •20.2. Организация обмена массивами данных
- •20.3. Мультиплексный канал
- •20.4. Селекторный канал
- •20.5. Устройства сопряжения - мультиплексоры передачи данных
- •Контрольные вопросы к главе 20
- •Глава 21. УСТРОЙСТВА ЗАЩИТЫ ОТ ОШИБОК В ПЕРЕДАВАЕМОЙ ИНФОРМАЦИИ
- •21.1. Причины возникновения ошибок в передаваемой информации
- •21.2. Краткая характеристика способов защиты от ошибок
- •21.3.Обнаруживающие коды - с проверкой на четность и итеративный код
- •21.4. Корректирующий код Хэмминга
- •21.5. Циклические коды
- •21.6. Циклический код Файра как средство коррекции пакетов ошибок
- •Контрольные вопросы к главе 21
- •ЗАКЛЮЧЕНИЕ
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Приложение 7
- •Приложение 8
- •Приложение 9
- •Приложение 10
- •Приложение 11
- •Приложение 12
- •Приложение 13
- •Приложение 14
- •Приложение 15
- •Приложение 16
- •Приложение 17
- •Приложение 18
- •Приложение 19
- •Приложение 20
- •Приложение 22
- •Приложение 23
- •Приложение 24
- •Приложение 25
- •Приложение 26
- •Предметный указатель
- •Список литературы
Глава 21. Устройства защиты от ошибок в передаваемой информации |
292 |
аппаратуры.
Опасность возникновения внутренних наводок возросла с внедрением БИС, СБИС особенно средней и большой сложности, вплоть до микропроцессорных наборов. Из-за увеличенной плотности элементов и схем сами ИС и межсоединения становятся источниками помех, которые передаются через возросшие паразитные емкости и индуктивности между проводниками или через проводимость изоляции. В зависимости от того, какой из этих параметров определяет в основном величину тока наводки, различают емкостные наводки, электромагнитные и гальванические. Величину тока электрической помехи Iп , наведенной через емкостную паразитную связь величиной С от источника помехи с амплитудой Uп и частотой fп, можно определить из выражения
Iп=2Uпπ fпС.
Аппаратура считается помехоустойчивой, если при воздействии помех допустимого уровня она продолжает выполнять свои функции без искажения информации (без ошибок).
21.2. Краткая характеристика способов защиты от ошибок
Основным способом повышения верности передачи дискретных сообщений является введение в передаваемую последовательность избыточности с целью обнаружения и исправления ошибок в принятой информации. Все устройства защиты от ошибок (УЗО) делятся на две группы: симплексные (без обратной связи) и дуплексные (с обратной связью).
В симплексных УЗО повышение верности может быть достигнуто тремя способами:
-путем многократного повторения символов,
-одновременной передачей одной и той же информации по нескольким параллельным каналам,
-применением кодов, исправляющих ошибки.
Многократное повторение является наиболее простым способом повышения верности, который состоит в том, что передатчик посылает в канал нечетное число раз одну и ту же информацию, а на приемной стороне производится сравнение между собой одноименных кодовых комбинаций (либо одноименных двоичных разрядов). Потребителю выдается тот символ (или бит), который был принят большее число раз (мажоритарный метод). Избыточность информации растет пропорционально количеству повторений одних и тех же символов, аналогично возрастают и затраты времени на передачу массива.
Вероятность ошибочного приема символа Ркк, состоящего из nк - разрядной комбинации, при трехкратном повторении и посимвольном сравнении не превышает величины, определяемой по формуле
Ркк≈ 3nк2Ро,
где Ро - вероятность ошибочного приема единичного элемента.
При пятикратном повторении nк - элементной комбинации эта вероятность равна:
Ркк≈ 10nк2Ро3.
При поразрядном сравнении принимаемых символов, состоящих из nк бит, вероятность ошибочной регистрации кодовой комбинации при трехкратном и пятикратном повторении соответственно равна
Ркк≈ 3nкРо2; Ркк≈ 10nкРо3.
Эти формулы справедливы при независимых ошибках в дискретном канале. При пакетировании ошибок (объединении одиночных ошибок в пакеты, в пачки) вероятность поражения соседних символов, а тем более бит, высока, что может привести к значительному снижению помехоустойчивости. Для устранения этого явления производят декорреляцию ошибок, увеличивая интервал между повторяемыми символами (битами), то есть следует повторять не отдельные символы блока, а их группы либо весь блок. Такой алгоритм пере-
Глава 21. Устройства защиты от ошибок в передаваемой информации |
293 |
дачи приводит к усложнению аппаратуры и увеличению временной задержки между передачей данных от источника и получением их потребителем.
Способ одновременной передачи по нескольким каналам по помехоустойчивости эквивалентен способу многократной передачи. Он предусматривает наличие нечетного количества каналов, по которым передаются одни и те же кодовые последовательности. На приемной стороне используется мажоритарный прием. Основное требование таких систем: наличие параллельных каналов с независимыми ошибками. Для обеспечения этого требования каналы связи должны быть разнесены географически или выбираться в разных линиях связи. Недостатком этого способа является резкое повышение стоимости системы передачи данных (СПД).
Наибольшей эффективностью в симплексных СПД обладает способ защиты от ошибок в передаваемой информации, основанный на использовании кодов с исправлением ошибок, называемых также исправляющими или корректирующими кодами. В таких системах передаваемый блок кроме информационных единичных элементов, полученных от источника информации, содержит и избыточные проверочные биты, формируемые кодирующим устройством на основании информационных разрядов по определенным правилам. На приемной стороне декодирующим устройством по тем же правилам осуществляются аналогичные проверки, при которых учитываются и проверочные элементы. В результате проверки определяется номер позиции в принятом блоке, значение которой необходимо в процессе исправления проинвертировать. Вероятность ошибочного приема символа зависит не только от вероятности ошибки в дискретном канале, но и от применяемого помехоустойчивого кода.
Помехоустойчивыми кодами называются коды с избыточностью, позволяющие обнаруживать и исправлять ошибки, возникающие в результате воздействия помех в принимаемых кодовых последовательностях. Корректирующая способность кода зависит от кодового расстояния d, численно равного минимальному числу элементов, которыми отличается любая кодовая комбинация от другой. В общем случае
d=tо +tи +1,
где tо и tи - число обнаруженных и исправленных ошибок соответственно, причем обязательно tо≥ tи. Если код только обнаруживает ошибки, то d=tо+1, а в случае только исправления d=2tи+1. Количество проверочных элементов r корректирующего кода зависит от вида кода, а число информационных элементов k=n-r, где n-длина двоичной последовательности, кодируемой помехоустойчивым кодом. Отношение r/n называется коэффициентом избыточности кода.
Пример 21.1. Выбрать способ защиты от ошибок, обеспечивающий вероятность побайтной передачи Ркк<1·10-6 при передаче данных по симплексному двухпроводному телефонному каналу связи со скоростью 1200 бит/с при условии, что ошибки на выходе дискретного канала группируются в пакеты длиной не более 12 бит, а минимальный интервал между пакетами составляет 3 с. Вероятность ошибки по элементам на выходе дискретного канала Ро<1·10-4.
Для исправления ошибок кратностью 12 наиболее целесообразно в данном случае применить способ многократной передачи информации. Так как пачка ошибок может поразить 3 байта, то повторять следует не менее трех знаков. При трехкратном повторении и поэлементном сравнении вероятность ошибки регистрации знака равна:
Ркк≈ 3nкРо2≈ 3·8(1·10-4)2=0,24·10-6<1·10-6.
Максимальная задержка выдачи информации потребителю при трехкратном повторении составит tз=24τ о=24·0,83≈ 20 мс, что вполне приемлемо для технических нужд.
21.3.Обнаруживающие коды - с проверкой на четность и итеративный код
Одним из простых кодов, позволяющих обнаруживать одиночные ошибки, является код с проверкой на четность. Он образуется путем добавления к передаваемой комбинации, состоящей из k информационных символов неизбыточного кода, одного контрольного бита
Глава 21. Устройства защиты от ошибок в передаваемой информации |
294 |
так, чтобы общее количество единиц в передаваемой комбинации было четным. В итоге общее количество элементов в передаваемой комбинации n=k+1. На приемной стороне производят проверку на четность. При четном числе единиц предполагается, что ошибок нет, и потребителю выдается k бит, а контрольный элемент отбрасывается. Аналогично строится код с проверкой на нечетность.
Кодирующие и декодирующие устройства кодов с защитой на четность - самые простые. Формирование контрольного бита осуществляется сумматором по модулю 2 (Т-триг- гером). Передаваемая в канал двоичная комбинация одновременно подается на вход Т-триг- гера. На соответствующей временной позиции импульсом с распределителя производится опрос сумматора, и при единичном состоянии последнего в канал подается “1” (дополняющая переданную последовательность до четного числа), а при нулевом - “0”. Аналогичная процедура производится на приемной стороне. Нулевое состояние Т-триггера в конце приема блока свидетельствует об отсутствии одиночных ошибок.
Минимальное кодовое расстояние кода d=2, поэтому код позволяет обнаруживать все одиночные ошибки, а кроме того, все случаи нечетного числа ошибок (3, 5, и т.д.).
Вероятность необнаружения ошибок для кода с проверкой на четность зависит от длины
блока n и вероятности ошибочного приема единичного элемента Р0:
Ркк≈ Сn2Ро2(1-Ро)n-2, Cnl=n!/[l!(n-l)1],
где Сnl - число сочетаний из n по l.
Как показывают расчеты по этим формулам, для обеспечения вероятности ошибки по символам менее 1·10-6 допустимая длина кодовой комбинации составляет несколько байт.
Итеративный код характеризуется наличием двух или более систем проверок внутри каждой кодовой комбинации, согласно ГОСТ 20687-75 он строится следующим образом. К семиэлементному коду КОИ-7 добавляют проверочный бит, который располагается в 8-й позиции. Элементы передаваемого блока и проверочные биты образуют матрицу:
а11 |
а12 |
а13 |
. . . а1n |
r1 |
|
а21 |
а22 |
а23 |
. . . |
а2n |
r2 |
. . . . . . . . . . . . . |
|||||
a71 |
a72 |
a73 |
. . . |
a7n |
r7 |
q1 |
q2 |
q3 |
. . . qn |
q(n+1), |
|
где аij (i=1, 2, . . .,7; j=1, 2, . . . , n) - информационные биты; q1, q2, q3, . . . , qn - проверочные биты знаков, образующие первую совокупность проверок. В конце матрицы стоят биты проверки на четность ri (i=1, 2, . . . , 7) которые являются суммой по модулю 2 всех элементов строки; r1 - r7 включается в знак проверки - это вторая совокупность проверок. К семи элементам знака добавляется восьмой проверочный бит q(n+1). Проверочные биты q1, q2, .
. ., q(n+1) формируются таким образом, чтобы число единиц в столбце было четным для асинхронных систем и нечетным - для синхронных. Каждый знак нужно передавать последовательно, начиная с первого бита aij и кончая восьмым проверочным.
Кодирующее устройство итеративного кода (рис. 21.5) содержит параллельный 8-раз- рядный сумматор по модулю 2 (D1), в котором формируется проверочный элемент столбца qj. Проверочный бит вместе с поступающей информационной кодовой комбинацией заносится в параллельно-последовательный регистр D3. Синхронизация записи осуществляется подачей управляющего импульса на вход С2. Сформированный байт подается на вход параллельно-последовательного сумматора по модулю 2 (D4), в котором осуществляется построчное суммирование передаваемых кодовых комбинаций. Операция суммирования в D4 синхронизируется импульсом, подаваемым на вход С в конце каждого восьмого такта. Поэлементная выдача байта данных в дискретный канал производится под действием сдвигающих тактовых импульсов, подаваемых на вход С1 и D3. Момент времени подачи ТИ и их количество определяются управляющим потенциалом, поступающим от устройства уп-
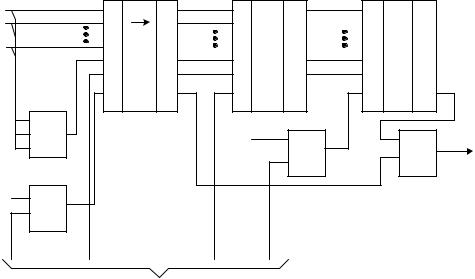
Глава 21. Устройства защиты от ошибок в передаваемой информации |
295 |
равления на вход схемы совпадения D2. В конце информационного блока контрольная сумма r1, r2, . . . , r7, q(n+1) переписывается в регистр сдвига D6 при наличии управляющего потенциала с УУ на втором входе D5 и выдается в последовательной форме на вход устройства преобразования сигналов (УПС).
В состав декодирующего устройства также входят сумматоры по модулю 2, осуществляющие проверку на четность поступающих байтов по столбцам и по строкам. Так как ошибка может быть обнаружена в любом столбце, то ее необходимо фиксировать в момент появления. Несоблюдение признака четности по строкам обнаруживается только по окончании блока.
Начальный знак блока НТ (начало текста) и символ СИН (синхронизация) не включают в суммирование. В блок включается комбинация КБ (конец блока), указывающая, что далее следует знак проверки матрицы.
a1 |
|
D3 |
|
D4 |
|
D6 |
|
D 0 |
RG Q 0 |
T M2 Q 0 |
D 0 |
RG |
|
||
a2 1 |
|
||||||
2 |
D 1 |
Q1 |
T |
|
|
|
|
a7 |
D 8 |
|
|
|
|
|
|
7 |
Q6 |
T |
Q6 |
D 6 |
|
|
|
|
D 7 |
|
|
||||
|
C2 |
Q7 |
T |
Q7 |
D 7 |
|
|
|
C1 |
Q8 |
C |
|
C |
Q7 |
|
|
D1 |
|
|
|
|||
|
M2 |
|
|
D5 |
|
|
|
|
q |
|
|
ТИ |
|
& |
На УПС |
|
|
|
& |
|
|||
ТИ |
|
|
|
|
|
D7 |
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D2
От УУ УЗО
Рис. 21.5. Кодирующее устройство итеративного кода
Кодовое расстояние итеративного кода d=4, он обнаруживает все ошибки кратности до трех и нечетной кратности, а также любой пакет ошибок длиной l+1, где l - длина строки матрицы кода. Недостатком итеративного кода, использующего проверку на четность по столбцам и строкам, является его высокая избыточность (≈ 15%). Однако кодирование и декодирование таких кодов очень просто реализуется программными методами, поэтому итеративные коды используются в аппаратуре передачи данных (АПД) с микропроцессорными УЗО. При более жестких требованиях по достоверности передачи данных применяют итеративный код с тремя проверками.
21.4. Корректирующий код Хэмминга
Код Хэмминга - один из наиболее эффективных кодов, позволяющих исправлять любую одиночную ошибку. Кодовое расстояние d=3. Код образуется путем дополнения информационной части передаваемого блока, состоящей из k бит, r проверочными элементами, причем в информационную часть при кодировании можно включать и служебные символы (номер, начало и конец блока), за исключением маркерных комбинаций, которые целесообразно располагать в начале блока. При выборе длины передаваемого блока n и количества проверочных элементов r следует руководствоваться неравенством 2r≥ n+1. Учитывая, что r=n-k, неравенство запишется в виде
Глава 21. Устройства защиты от ошибок в передаваемой информации |
296 |
2k<=2n/(n+1),
где n и k - целые числа. Неравенство является исходным для определения длины кодовой комбинации по заданному числу k. Из этих неравенств следует, например, что пять контрольных разрядов позволяют передавать в коде Хэмминга от 11 до 26 информационных разрядов и т.д.
Первый проверочный элемент П1 кода Хэмминга (КХ) образуется суммированием по модулю 2 всех нечетных бит блока, начиная с первого:
П1=а1+а3+а5+а7+ . . . .
Результат проверки П2 определяет второй разряд проверочной комбинации, называемой также синдромом ошибки. Он вычисляется суммированием тех бит блока, номера которых соответствуют n-разрядным двоичным числам, имеющим единицу во втором разряде, то есть
П2=а2+а3+а6+а7+а10+а11+ . . . .
Третья проверка П3 охватывает разряды, номера которых соответствуют n-разрядным числам, имеющим единицу в третьем разряде. Аналогично находятся разряды, охватываемые четвертой, пятой и т.д. проверками:
П3=а4+а5+а6+а7+а12+а13+а14+а15+ . . . ,
П4=а8+а9+а10+а11+а12+а13+а14+а15+ . . . ,
П5=а16+а17+а18+а19+а20+ . . . .
В таблице 21.2 показан пример построения КХ для семиразрядного слова.
Место расположения проверочных элементов не имеет значения, их можно размещать перед, после и чередуя с информационными символами. Если их расположить на местах, кратных степени 2, то есть на позициях 1, 2, 4, 8 и так далее, то код двоичного числа, образованного проверочными элементами, на приемной стороне будет указывать номер разряда, в котором произошла ошибка.
Таблица 21.2. Построение кода Хэмминга
_________________________________________________
Номер разрядов кодового слова Проверочные разряды
_________________________________________________
Десятичный Двоичный 1 2 3
_________________________________________________
1 |
0001 |
* |
|
|
2 |
0010 |
|
* |
|
3 |
0011 |
* |
* |
|
4 |
0100 |
|
|
* |
5 |
0101 |
* |
|
* |
6 |
0110 |
|
* |
* |
7 |
0111 |
* |
* |
* |
__________________________________________________
Контроль по КХ реализуется с помощью набора схем проверки на четность, которые при кодировании определяют контрольные разряды, а при декодировании формируют корректирующее число.
Поскольку основной операцией в кодирующих и декодирующих устройствах КХ является суммирование по модулю 2, то их схемы отличаются от схем кодеров итеративного кода образованием проверочных элементов. Для упрощения технической реализации (исключение многоразрядных параллельных сумматоров, входного накопительного регистра) вначале посылают в канал информационные биты, а затем проверочные. При таком способе формирование контрольных элементов можно осуществлять с помощью одноразрядных
Глава 21. Устройства защиты от ошибок в передаваемой информации |
297 |
последовательных сумматоров по модулю 2 одновременно с передачей информационных разрядов. Чтобы сохранить корректирующие свойства КХ, необходимо произвести перестановку разрядов в проверочных равенствах с учетом изменения номеров суммируемых элементов за счет вынесения в конец блока проверочных битов. При такой перестановке уравнения проверки будут охватывать следующие разряды:
П1 : 1, 2, 4, 5, 7, 9, 11, 12, 14, . . . ; П2 : 1, 3, 4, 6, 7, 10, 11, 13, 14, . . . ; П3 : 2, 3, 4, 8, 9, 10, 11, . . . ; П4 : 5, 6, 7, 8, 9, 10, 11, . . . .
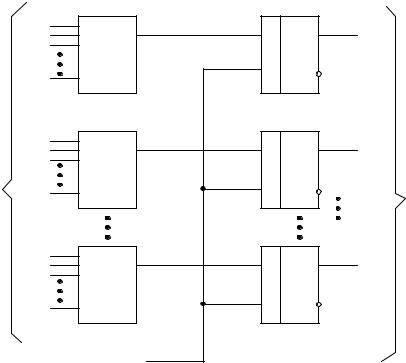
Бит первой проверки будет располагаться на (k+1)-й позиции блока, второй - на (k+2)- й, последний - на n-й позиции. На рис. 21.6 приведена схема одного из вариантов формирования проверочных битов КХ, которая может быть использована как в кодере, так и в декодере. Информационные элементы, поступающие от источника, подаются на счетные входы Т-триггеров (сумматоров по модулю 2) и через УПС - в канал связи. Количество триггеров равно числу контрольных элементов r . Синхронизация суммирования осуществляется импульсами с распределителя, которые объединяются схемами ИЛИ. Входы первого элемента ИЛИ соединяются с выходами распределителя в соответствии с первой проверкой П1, второй - проверкой П2 и так далее. Таким образом обеспечивается суммирование на Т- триггерах тех битов, номера которых определяются соответствующими проверками. После прихода последнего k-го информационного элемента в сумматорах будет зафиксировано r проверочных элементов. В кодирующем устройстве эти биты преобразовываются в последовательную форму и через УПС поступают в канал связи. На приемной стороне вместе с информационными суммированию подвергаются и проверочные элементы. Полученная r- разрядная кодовая комбинация (синдром ошибки) подается на дешифратор, определяющий номер разряда, в котором произошла ошибка. Данный дешифратор отличается от классического дешифратора КХ и должен учитывать перестановки контрольных элементов, произведенные при кодировании.
От распределителя
1 |
1 |
С |
Т |
Q1 |
2 |
||||
4 |
|
|
|
|
|
|
Т |
|
|
1 |
1 |
С |
Т |
Q2 |
3 |
||||
4 |
|
|
|
|
|
|
Т |
|
Проверочные |
|
|
|
биты |
|
|
|
|
|
|
|
1 |
С |
Т |
Qr |
|
|
Т |
|
|
|
|
Вход |
|
|
Рис. 21.6. Схема формирования проверочных элементов кода Хэмминга
