
- •Предисловие
- •Введение
- •1. Роль и место прогнозирования при обосновании направления развития систем
- •1.1. Классификация методов прогнозирования
- •1.2. Краткая характеристика методов прогнозирования
- •1.3. Виды прогнозов. Основные термины и определения прогностики
- •2. Прогнозная экстраполяция. Оценка параметров прогнозных моделей методом наименьших квадратов. Точность и достоверность прогноза
- •2.1. Оценка параметров прогнозной модели методом наименьших квадратов
- •2.2. Точность и достоверность прогноза
- •3. Уравнения линеаризуемых трендов и трендов, сводящихся к модифицированной экспоненте
- •3.1. Парные регрессии, сводящиеся к линейному тренду
- •3.2. Парные регрессии, сводящиеся к модифицированной экспоненте
- •3.3. Выбор оптимального вида прогнозной модели
- •3.4. Проверка прогнозной модели на автокорреляцию ошибок
- •4. Многомерное параметрическое прогнозирование. Метод многомерной линейной экстраполяции
- •5. Метод экспоненциального сглаживания. Выбор постоянной сглаживания
- •5.1. Сущность метода экспоненциального сглаживания
- •5.2. Определение параметров прогнозной модели методом экспоненциального сглаживания
- •5.3. Выбор начальных условий и определение постоянной сглаживания
- •6. Вероятностные методы прогнозирования
- •6.1. Приложение теории суммирования случайного числа независимых случайных величин в задачах прогнозирования
- •6.2. Ориентированный процесс случайного блуждания как метод вероятностного моделирования
- •7. Математические модели процессов эволюционного развития техники
- •7.1. Математическое моделирование процессов развития техники
- •7.2. Прогнозная математическая модель динамики замещения
- •8. Экспертные методы прогнозирования. Морфологический анализ. Прогнозирование технического облика образца изделия
- •8.1. Морфологический анализ
- •8.2. Прогнозирование технического облика перспективного образца
- •8.3. Другие методы экспертного прогнозирования
- •3. Метод «мозговой атаки» («мозгового штурма»).
- •9. Методы выявления «сезонной» составляющей в рядах динамики
- •9.1. Выравнивание рядом Фурье
- •9.2. Измерение колеблемости в рядах динамики
- •9.3. Выявление и измерение сезонных колебаний
- •10. Зависимость средней ошибки прогноза от периода предыстории и величины прогнозируемого периода
- •10.1. Обоснование периода упреждения
- •Заключение
- •Библиографический список
- •Предметный указатель
- •Приложение 1 Приложение 2 Квантили распределения максимального относительного отклонения
- •Приложение 3 Квантили распределения величины
- •Приложение 4 Приложение 5
- •Приложение 6 Приложение 6
- •Приложение 7
- •191186, Санкт-Петербург, ул. Миллионная, 5
2. Прогнозная экстраполяция. Оценка параметров прогнозных моделей методом наименьших квадратов. Точность и достоверность прогноза
Основу экстраполяционных методов прогнозирования составляет изучение временных рядов, представляющих собой упорядоченные во времени наборы измерений тех или иных характеристик исследуемого объекта, процесса. Временной ряд yi может быть представлен в следующем виде:
Yt=xt+et ,
где xt – детерминированная неслучайная компонента процесса;
et – стохастическая случайная компонента процесса.
Если детерминированная компонента (тренд) xt характеризует общее направление развития, основную тенденцию временного ряда, то стохастическая компонента et отражает случайные колебания, или шумы, процесса. Обе составляющие процесса определяются каким-либо функциональным механизмом, характеризующим их поведение во времени. Задача прогноза состоит в определении вида экстраполирующих функций xt и et на основе исходных эмпирических данных.
Первым этапом экстраполяции тренда является выбор оптимального вида функции, описывающей эмпирический ряд. Для этого проводятся предварительная обработка и преобразование исходных данных в целях облегчения выбора вида тренда путем сглаживания и выравнивания временного ряда, а также формального и логического анализа особенностей процесса. Следующим этапом является расчет параметров выбранной экстраполяционной функции.
Наиболее распространенными методами оценки параметров зависимостей является метод наименьших квадратов и его модификации, метод экспоненциального сглаживания и метод вероятностного моделирования.
2.1. Оценка параметров прогнозной модели методом наименьших квадратов
Сущность метода наименьших квадратов (МНК) состоит в отыскании параметров модели тренда, минимизирующих ее отклонение от точек исходного временного ряда, то есть
![]() , (2.1)
, (2.1)
где
![]() – расчетные значения исходного ряда;
– расчетные значения исходного ряда;
![]() – фактические
значения исходного ряда;
– фактические
значения исходного ряда;
![]() – число наблюдений.
– число наблюдений.
Если модель тренда представить в виде
![]() ,
,
где ![]() –
независимые переменные;
–
независимые переменные;
![]() – параметры модели;
– параметры модели;
![]() – время,
– время,
то,
для того, чтобы найти параметры модели,
удовлетворяющие условию (2.1), необходимо
приравнять к нулю первые производные
величины S
по каждому из коэффициентов
![]() .
Решая полученную систему уравнений с
k
неизвестными,
находим значения коэффициентов a.
.
Решая полученную систему уравнений с
k
неизвестными,
находим значения коэффициентов a.
Использование процедуры оценки, основанной на МНК, предполагает обязательное удовлетворение целого ряда предпосылок, невыполнение которых может привести к значительным ошибкам.
Нормальность. Случайные ошибки (значение случайной компоненты) имеют нормальное распределение.
Случайные ошибки имеют нулевую среднюю, конечные дисперсию и ковариации.
Дисперсии каждой случайной ошибки одинаковы, их величины независимы от значений наблюдаемых переменных.
Отсутствие автокорреляции ошибок, то есть значения ошибок, различных наблюдений независимы друг от друга.
Значение наблюдаемых переменных свободны от ошибок измерения и имеют конечные средние значение и дисперсии.
В практических
исследованиях в качестве модели тренда
в основном используют следующие
функции: линейную
![]() ;
квадратичную
;
квадратичную
![]() ;
параболу третьей степени
;
параболу третьей степени
![]() ;
степенную
;
степенную
![]() ;
показательную
;
показательную
![]() ;
экспоненциальную
;
экспоненциальную
![]() ;
модифицированную экспоненциальную
;
модифицированную экспоненциальную
![]() ;
логистическую
;
логистическую
![]() .
.
Особенно широко применяется линейная, или линеаризуемая, то есть сводимая к линейной, форма, как наиболее простая и в достаточной степени удовлетворяющая исходным данным. В этом случае при постановке динамической задачи прогнозирования уравнение регрессии имеет вид
![]() , (2.2)
, (2.2)
где
![]() – вычисленное значение
– вычисленное значение
![]() ,
соответствующее моменту времени t.
,
соответствующее моменту времени t.
а и b – константы, которые обращают сумму квадратов отклонений фактических значений от вычисленных в минимум.
Используя метод наименьших квадратов, можно составить систему уравнений:
 ,
,
решая которую, получим уже систему нормальных уравнений:
 (2.3)
(2.3)
Следовательно,
 ,
,
где b называют коэффициентом регрессии (не путать с коэффициентом корреляции), он характеризует наклон линии регрессии (тангенс угла наклона);

или
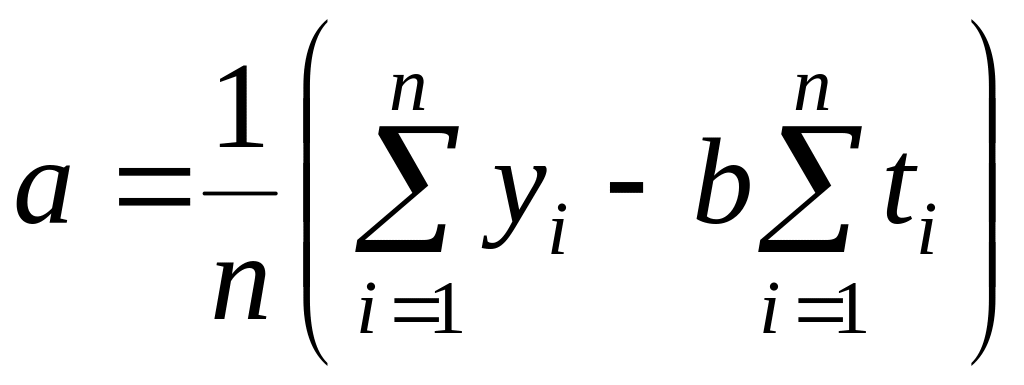 ,
,
где
a
называют начальным или свободным
коэффициентом, он характеризует уровень
пересечения линии регрессии с осью
ординат y,
то есть равен
при
![]() .
.
Система нормальных уравнений существенно упрощается, если начало отсчета времени перенести в середину динамического ряда путем преобразования независимой переменной:
![]() ,
,
тогда для линейной модели
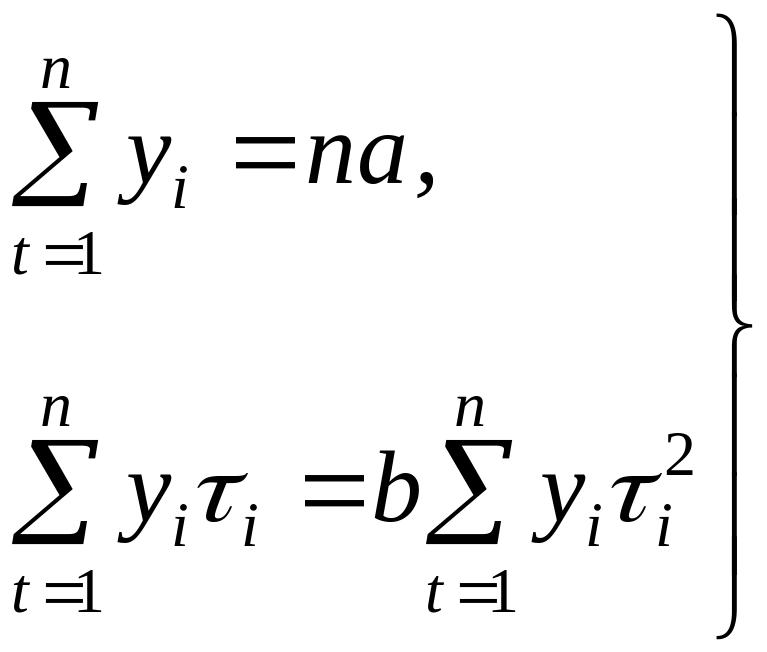
и
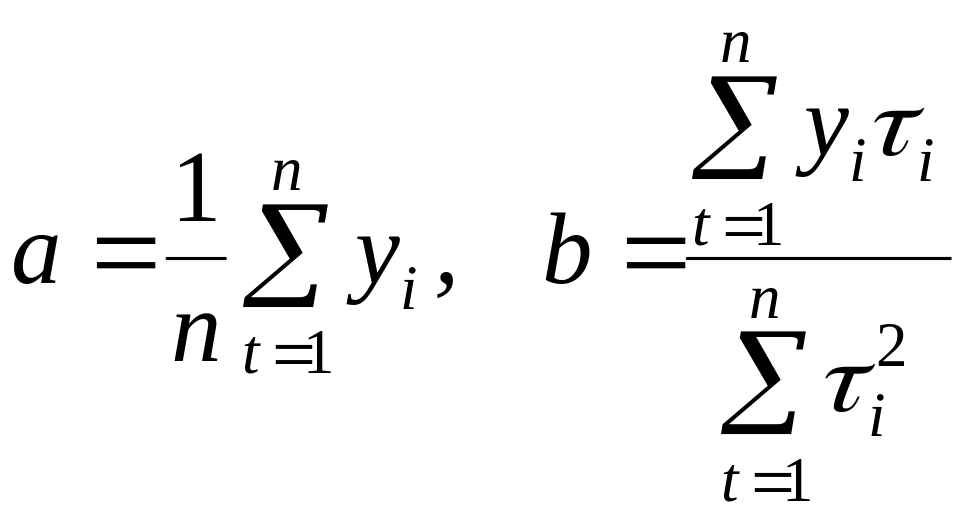 .
.
После того, как определены коэффициенты модели (2.2), точечный прогноз для момента времени tk может быть осуществлен по уравнению регрессии
 .
.
Рассмотренный механизм метода наименьших квадратов позволяет с необходимой точностью аппроксимировать действительное развитие процесса с помощью полиномиального тренда, то есть представить зависимую переменную y как функцию времени в виде многочлена
![]() ,
,
где
![]() – параметры;
– параметры;
– время;
![]() – степень полинома.
– степень полинома.
Оценки параметров
![]() получают, исходя из решения системы
нормальных уравнений, развернутая
запись которых имеет вид (здесь, как и
ранее, переменные xi
заменены на
характеристики времени ti;
знак
означает
получают, исходя из решения системы
нормальных уравнений, развернутая
запись которых имеет вид (здесь, как и
ранее, переменные xi
заменены на
характеристики времени ti;
знак
означает
суммирование
![]() ):
):
![]() (2.4)
(2.4)
где n – число членов в динамическом ряду.
Система (2.4),
состоящая из
уравнений,
содержит в качестве известных величин
![]() ,
,
![]() ,
…,
,
…,
![]() (то есть суммы наблюдаемых значений
уровней динамического ряда, умноженные
на показатели времени в степени 0,
1, 2, …,
и
неизвестных величин aj.
(то есть суммы наблюдаемых значений
уровней динамического ряда, умноженные
на показатели времени в степени 0,
1, 2, …,
и
неизвестных величин aj.
Необходимо отметить, что системы для оценивания параметров полиномов невысоких степеней достаточно просты. Обозначим последовательные параметры полиномов как a, b, c, d. Тогда нормальные уравнения для оценивания квадратичной модели [нормальные уравнения для оценивания прямой см. систему (2.3)] примут вид
![]() ,
,
для параболы третьей степени получим
![]() .
.
Поскольку полиномы выше третьей степени при обработке динамических рядов встречаются крайне редко, то нормальные уравнения для них приводить не будем.
Составление
нормальных уравнений можно упростить,
воспользовавшись тем, что величины
![]() ,
,
![]() ,
… не зависят от конкретных значений
(уровней) динамического ряда. Если
последний состоит из уровней, равноотстоящих
друг от друга (а именно с такими рядами
чаще всего имеет дело исследователь),
то суммы
,
,
… являются функциями только числа
членов в динамическом ряду. Для них
легко получить расчетные формулы, в
частности
,
… не зависят от конкретных значений
(уровней) динамического ряда. Если
последний состоит из уровней, равноотстоящих
друг от друга (а именно с такими рядами
чаще всего имеет дело исследователь),
то суммы
,
,
… являются функциями только числа
членов в динамическом ряду. Для них
легко получить расчетные формулы, в
частности
![]()
![]()
![]()
![]()
![]()
![]() .
.
Во всех приведенных здесь формулах суммирование производится от t=1 до t=n. Значения сумм табулированы для широкого диапазона величин n.
Рассмотрим для примера оценки параметров прямой динамический ряд типовых объектов; соответствующие уровни yt и произведения ytt приведены в табл. 2.1.
Таблица 2.1. Сводная таблица для оценки параметров
T, год |
1973 |
1975 |
1977 |
1979 |
1981 |
1983 |
1985 |
t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
yt, шт. |
227 |
219 |
209 |
197 |
193 |
200 |
199 |
ytt |
227 |
438 |
627 |
788 |
965 |
1200 |
1393 |
|
|
|
|
|
|
|
|
T, год |
1987 |
1989 |
1991 |
1993 |
1995 |
1997 |
1999 |
t |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
yt, шт. |
197 |
191 |
177 |
175 |
167 |
193 |
144 |
ytt |
1576 |
1719 |
1770 |
1925 |
2004 |
2509 |
2016 |
![]() ,
,
![]()
В соответствии с вышеприведенными формулами
![]() ;
;
![]() .
.
В соответствии с системой уравнений (2.3) систему нормальных уравнений запишем в виде
2683 = а · 14 + b · 105; 19157= а · 115 + b · 1015.
Решение этой системы дает
![]() ;
;
![]() .
.
Уравнение регрессии, следовательно, имеет вид
![]() ,
,
а точечный прогноз, например, на 2000 год (tk=17) будет равен
![]() объектов.
объектов.
Таким образом, собственно экстраполяция дает точечную прогностическую оценку. Интуитивно ощущается недостаточность такой оценки и необходимость получения интервальной оценки, с тем чтобы прогноз, охватывая некоторый интервал значений прогнозируемой переменной, был бы более надежным или, другими словами, более достоверным и точным.
