
- •Тема 3.2. Числовая последовательность и ее предел Оглавление
- •1. Понятие числовой последовательности и ее предела
- •1.1. Понятие расстояния. Абсолютная величина (модуль) числа и его свойства
- •1.2. Определение числовой последовательности
- •1.3. Предел числовой последовательности
- •2. Сходящиеся последовательности и их основные свойства
- •2.5. Теорема о вложенных промежутках
- •2.6. Теорема о сжатой переменной (принцип двух милиционеров)
- •2.7. Теорема о предельном переходе в неравенстве
- •2.8. Теоремы о пределах ч. П. Полученных с использованием арифметических операций
- •3.2. Связь бесконечно малых и бесконечно больших величин
- •3.3. Типы неопределенных выражений
- •4. Число
Тема 3.2. Числовая последовательность и ее предел Оглавление
1. Понятие числовой последовательности и ее предела
1.1. Понятие расстояния. Абсолютная величина (модуль) числа и его свойства
Абсолютной
величиной(модулем) действительного
числа называется
называется
 .
.
Покажем, чтосоотношения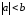 (где
(где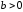 )
и
)
и равносильны
равносильны
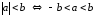 . (1)
. (1)
Действительно,
существует две возможности:
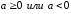 .
Пусть
.
Пусть .
Тогда
.
Тогда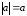 и поэтому
и поэтому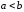 .
Тем более
.
Тем более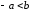 .
Умножая последнее соотношение на -1
получим,
.
Умножая последнее соотношение на -1
получим,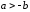 .
Объединяя полученные два неравенства
в одно, получим
.
Объединяя полученные два неравенства
в одно, получим
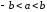 .
.
Аналогично рассматривается другая возможность, а также обратное утверждение.
Из определения модуля следует
 . (2)
. (2)
Прежде всего, отметим справедливость следующих неравенств:
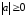 ;
; ;
;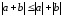 ;
;
Для модулей следующие неравенства находят широкое применение
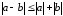 ;
; ;
;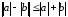 ;
; ;
;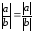 .
.
В качестве примера докажем неравенство 3. Очевидно, выполняются следующие соотношения
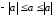 и
и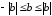 .
.
Сложим почленно оба неравенства. В результате получим
 .
.
Что эквивалентно
в соответствии с формулой (1)
 .
.
Неравенство 4
доказывается заменой в неравенстве 3
 на
на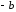 .
.
Неравенство 5 доказывается с использованием очевидного соотношения
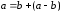 .
.
Используя неравенство 3 получаем
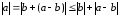 ,
,
откуда следует неравенство (5).
Неравенство 6 доказывается с помощью следующих простых соотношений

Расстояниеммежду числами и
и называется
называется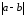 .
.
1.2. Определение числовой последовательности
Рассмотрим натуральные числа, расположенные по возрастанию
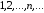 .
.
Каждому натуральному числу сопоставим вещественное число. В результате получим числовую последовательность в виде
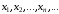 (1)
(1)
В числовой
последовательности (1) индекс при
вещественном числе совпадает с
натуральным числом и имеет смысл номера
члена последовательности. Нумерация
членов последовательности начинается
с единицы. Этот индекс упорядочивает
члены числовой последовательности.
Говорят, что член числовой последовательности
 является последующим по отношению к
является последующим по отношению к ,
если
,
если .
Член
.
Член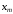 называют также предшествующим. Числовая
последовательность может рассматриваться
как функция натурального аргумента.
называют также предшествующим. Числовая
последовательность может рассматриваться
как функция натурального аргумента.
Примеры числовых последовательностей.
Арифметическая прогрессия
Номер члена числовой последовательности
Член числовой последовательности
1
a
2
a+d
3
a+2d
…
…
n
a+(n-1)d
…
…
Геометрическая прогрессия
|
Номер члена числовой последовательности |
Член числовой последовательности |
|
1 |
a |
|
2 |
aq |
|
3 |
aq2 |
|
… |
… |
|
n |
aqn-1 |
|
… |
… |
Запись
 отождествляют с любым членом
последовательности и называют ееобщим
членом.
отождествляют с любым членом
последовательности и называют ееобщим
членом.
Для арифметической прогрессии общий член представляется выражением
 , (2)
, (2)
а для геометрической прогрессии –
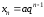 . (3)
. (3)
1.3. Предел числовой последовательности
Число
 называетсяпределомч.п.
называетсяпределомч.п.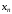 ,
если для любого, в том числе сколь угодно
малого, положительного числа
,
если для любого, в том числе сколь угодно
малого, положительного числа найдется номер
найдется номер ,
зависящий от
,
зависящий от ,
такой, что для любых
,
такой, что для любых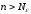 выполняется неравенство
выполняется неравенство
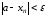 .
.
Предел ч.п. записывают в виде
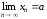 ,
,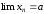 ,
,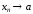 ,
,
и
при этом говорят, что переменная
 стремится к
стремится к или числовая последовательностьсходитсяк
или числовая последовательностьсходитсяк .
Точка
.
Точка является точкой сгущения последовательности,
так как за пределами любой ее окрестности
оказывается ограниченное количество
членов, а неограниченное - внутри нее.
Числовая последовательность, имеющая
предел называетсясходящейся, а не
имеющая предел –расходящейся.
является точкой сгущения последовательности,
так как за пределами любой ее окрестности
оказывается ограниченное количество
членов, а неограниченное - внутри нее.
Числовая последовательность, имеющая
предел называетсясходящейся, а не
имеющая предел –расходящейся.
Коротко определение предела числовой последовательности записывается в виде
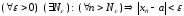 .
.
Ч. п.
 называетсявозрастающей, если
называетсявозрастающей, если
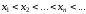 .
.
Ч. п.
 называетсянеубывающей, если
называетсянеубывающей, если
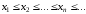 .
.
Аналогично определяется понятие убывающейиневозрастающейпоследовательности.
Ч. п., изменяющиеся в одном направлении, называются монотонными.
