4. Многомерное параметрическое прогнозирование. Метод многомерной линейной экстраполяции

Как отмечалось выше, различают две задачи экстраполяции – статическую и динамическую. Во втором случае задача экстраполяции сводится к прогнозированию поведения процесса во времени, то есть по его наблюдаемому отрезку и на основе каких-то априорных данных следует оценить дальнейшее поведение процесса во времени.

Статическая экстраполяция связана с параметрическим прогнозированием на плоскости или с прогнозированием в пространстве. Это означает, что аргументом здесь является вектор параметров и данный вид экстраполяции состоит в оценке значений векторного поля по отдельным наблюдениям.

Содержательную задачу многомерной параметрической экстраполяции, или, другими словами, пространственной экстраполяции, удобно описывать в следующих терминах. Пусть имеется конечное множество ситуаций – точек в пространстве ситуаций, где определены в ретроспекции некоторые решения (в общем виде – численные векторы). Задача экстраполяции состоит в том, чтобы оценить значение вектора решения в ситуации, которой не содержится в указанном множестве.

В последнее время для решения такого рода задач все большее применение находит так называемый метод многомерной линейной экстраполяции (ММЛЭ).

Задачу прогнозирования часто можно представить как задачу проектирования, то есть преобразования технического задания (объема предпрогнозной информации) в проект (прогноз). Если техническое задание обозначить вектором Х, а проект – Y, то процесс проектирования (прогнозирования) реализует преобразование

,

где – некоторая процедура проектирования.

Для автоматизации этого процесса необходимо формализовать процедуру . Это можно сделать двояким образом.

С одной стороны, можно вскрыть причинно-следственный механизм (правила проектирования), формализовать его и, запрограммировав соответствующим образом ЭВМ, получить с ее помощью проекты Y по техническим заданиям Х. Однако, как легко заметить, этот подход требует детального изучения процесса и реализуется лишь для очень простых конкретных задач.

Можно поступить иначе. Обычно имеется опыт проектирования изделий такого ряда, то есть матрица из n прецедентов (образцов-аналогов)

,

где – i-е задание на проектирование;

– проект, разработанный «старым» способом по этому заданию, то есть

.

Тогда, экстраполируя этот опыт (ретроспективную информацию) на новое техническое задание (новый вектор параметров) , можно получить с некоторой погрешностью, но сразу проект (прогноз) .

Таким образом, экстраполяция сводится к оценке значения и и матрице прецедентов , где F – алгоритм экстраполяции.

Отметим, что если X и Y измеряются в метрических шкалах и являются векторами

,

,

то таблицу прецедентов можно представить в виде числовой матрицы

:

.

Выбор алгоритма экстраполяции F , очевидно, зависит от количества имеющейся информации. Пусть нам известно только k прецедентов, и . Если число k достаточно велико по сравнению с размерностью вектора , то задачу можно решить m-кратным применением метода наименьших квадратов.

Если число наблюдений k соизмеримо с размерностью вектора X, то можно также решить задачу путем построения линейной модели

. (4.1)

Интерес представляет случай, когда число k наблюдений мало и недостаточно для априорного построения линейной модели, то есть

.

Решим задачу экстраполяции в этих условиях информационной недостаточности.

Множество векторов всех возможных ситуаций X обозначим через {X}, а соответствующее множество векторов Y решений – через {Y}. Линейную модель вида (4.1) построим на подмножествах векторов { } и { }, образованных исходя из реальных наблюдений

, , (4.2)

где символ «» обозначает соответствие.

Исходя из того, что элементы линейного пространства могут быть представлены в виде полиномов степени не выше , запишем уравнения для элементов векторных подмножеств { } и { }:

;

;

где и – коэффициенты пропорциональности.

Для доопределения этих функций на подмножествах { } и { } введем дополнительно две гипотезы.

I. Преобразование  линейно. Тогда для удовлетворения соответствия (4.2) следует положить

, .

II. Каждому вектору ставится в соответствие такой вектор , который доставляет минимум функции близости:

.

Таким образом, сформулируем полученный алгоритм решения задачи:

• преобразуем (гипотеза 2);

• отображаем (гипотеза 1);

• отождествляем .

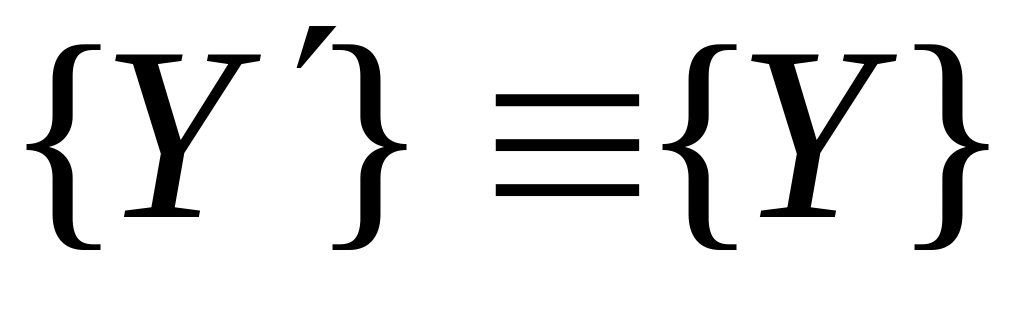Проиллюстрируем идею метода на простом примере двумерного пространства ситуаций.

Для построения алгоритма экстраполяции введем два линейных параметризованных пространства (рис. 4.1): двумерное пространство ситуаций X, где каждая ситуация определяется парой параметров и , и пространство решений Y, в котором каждое решение определяется двумя параметрами: и .

Предположим, что известны две проектные ситуации и , которым в пространстве решений соответствуют решения и .

З адача ставится следующим образом: дана проектная ситуация и нужно найти для нее решение , располагая только указанной ситуацией.

Рис. 4.1. Графическая интерпретация нахождения: а) проектной ситуации ; б) проектного решения , соответствующего ситуации

Через известные ситуации проводим прямую линию, являющуюся подпространством проектных ситуаций { }, через точки и – линию, являющуюся подпространством решений { } (рис. 4.1). Для новой проектной ситуации определим ближайшую точку на подпространстве ситуаций, для чего опустим перпендикуляр из точки на линию . Получим точку , являющуюся отображением точки на подпространстве ситуаций, которая делит отрезок в определенной пропорции. Разделив отрезок в подпространстве { } в этой же пропорции, получим проектное решение , соответствующее ситуации .

В соответствии с изложенным алгоритмом подпространства ситуаций и решений находим { }, { }по следующим формулам

;

,

где и – коэффициенты пропорциональности.

Так как = , то

,

где определяется, исходя из минимума функции близости.

Решение в числовом виде рассмотрим на основе модельного примера в трехмерном пространстве.

Имеются две проектные функции: и , для которых известны решения и . Необходимо найти новое решение для ситуации .

Условия задачи приведены в табл. 4.1.

Таблица 4.1. Условия задачи

Yi	Xi	x1	x2	x3
34,5	X1	2,0	3,0	1,5
49,9	X2	4,0	4,5	2,7
65,0	X3	5,5	6,0	4,0

Значение , определенное по заданному тест-базису, используем для оценки погрешности метода экстраполяции.

Так как , то

Вводим в рассмотрение функцию близости:

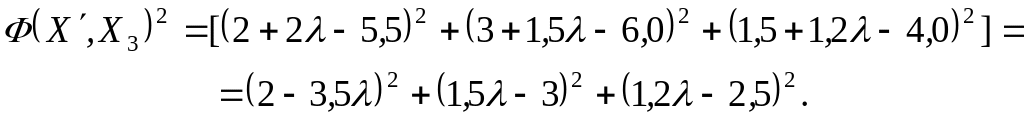
Минимизируем функцию близости, для чего определим ее производную по параметру :

,

откуда .

.

Таким образом, оценка погрешности для данного примера %.

Рассмотрим пример в пятимерном пространстве.

Исследователю известно три ретроспективные ситуации: , для которых известны выходные характеристики системы. Требуется найти оптимальную выходную характеристику системы для новой ситуации , Условия задачи приведены в табл. 4.2.

Как и в предыдущем примере, полагаем, что в ситуации известно точное значение выходной характеристики системы.

Решим задачу в двух вариантах. Вначале воспользуемся информацией по двум проектным ситуациям: и .

Алгоритм решения задачи аналогичен рассмотренному ранее, то есть вначале составляем подпространство известных ситуаций:

.

Формируем квадратичную функцию близости новой ситуации к подпространству :

.

Таблица 4.2. Исходные данные

19,75		2,0	1,0	1,5	2,5	1,0
39,00		3,0	2,5	3,5	3,0	2,0
47,25		4,0	3,5	5,0	5,0	3,0
85,50		5,0	8,0	6,0	6,0	5,0

Минимизируем квадратичную функцию близости, для чего находим производную по и приравниваем ее к нулю:

.

Решая уравнение, находим параметр .

По формуле экстраполяции, отождествляя , находим выходную

характеристику системы в проектной ситуации :

.

Зная точное значение выходной характеристики системы, оцениваем относительную погрешность экстраполяции %.

Решим эту же задачу, используя более полную информацию – проектные ситуации , и .

Как и в первом случае, составляем подпространство известных ситуаций:

вводим квадратичную функцию близости новой ситуации к подпространству :

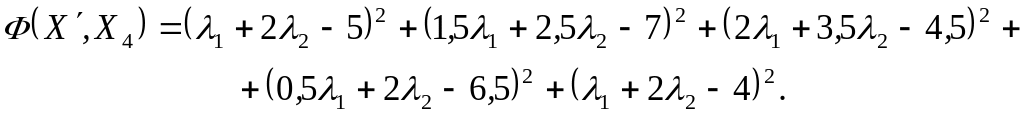
Минимизируем функцию близости, для чего приравниваем производную по переменным параметрам и к нулю:

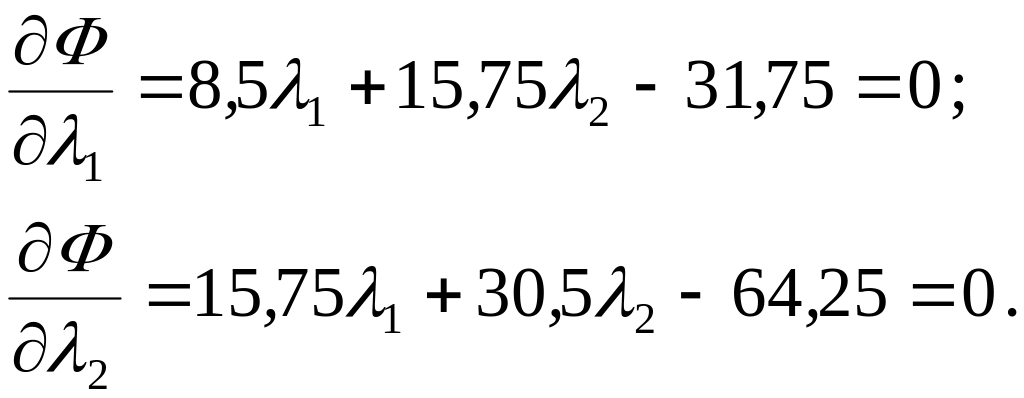
Решая систему уравнений, находим переменные параметры и , минимизирующие функцию близости:

; .

Построив подпространство решений по формуле

и вводя тождества , , находим

.

Используя точное значение модельной задачи, оценим относительную погрешность экстраполяции %.

Сравнивая результаты экстраполяции характеристик системы по двум и по трем аналогам, видим, что погрешность экстраполяции снизилась с 19,1 до 2,7 %.

Таким образом, рассмотренный метод применим для восстановления линейной функции в случае малого числа наблюдений.

Если восстанавливаемая функция нелинейна, метод можно применять при любом числе наблюдений. В этом случае значение функции в новой ситуации определяется не по всем имеющимся наблюдениям, а лишь по ближайшим к новой ситуации. В результате осуществляется локально-линейное приближение нелинейной функции.

Кроме задач прогнозирования, метод применим для восстановления числовых таблиц, для оценки числовых характеристик функций, для решения задач квалиметрии и тому подобных.

В табл. 4.3 представлены в относительных единицах (по отношению к характеристикам «Онест Джон») тенденции роста качественных характеристик основных элементов, а также технического уровня летательных аппаратов США.

Таблица 4.3. Тенденции роста качественных характеристик РК

Наименование ЛА	Год принятия	Элементы летат. аппарата				Технический уровень Q
		СУ	БЧ	ДУ	Корпус материала
«Онест Джон»	1950	1	1	1	1	1
«Ланс»	1970	4	3	3	2	4
«Ланс-2»	1990	10	8	6	5	8
Единая система	2010	15	12	8	7	12

В качестве контрольного для проверки точности алгоритма используем значение .

Таким образом, имеются три альтернативы , и , для которых найдены значения обобщенного показателя , и .

Необходимо определить показатель технического уровня системы с параметрами .

Формируем подпространство известных ситуаций:

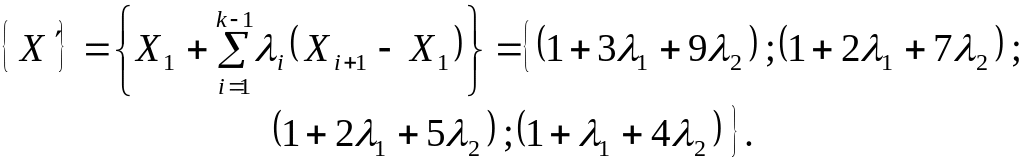
Определим квадратичную функцию близости новой ситуации к подпространству :

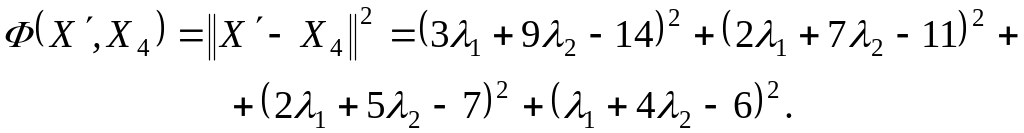
Решая систему уравнений, находим параметры, минимизирующие функцию близости:

; .

Построив подпространство решений по формуле

и вводя тождества , , находим экстраполированную характеристику уровня альтернативы , определяем относительную погрешность экстраполяции %.

При предположении, что восстанавливаемая функция нелинейна, используем лишь ближайшие лишь к новой ситуации наблюдения, то есть и . Тогда

,

минимизируя

,

получим .

Решение для ситуации находим по экстраполяционной формуле

.

В этом случае относительная погрешность экстраполяции %.

При решении методом пропорционального сдвига

;

Минимизируя эту функцию по p и , получим ; . Тогда для ситуации

; %.

Таким образом, алгоритм многомерной линейной экстраполяции позволяет с удовлетворительной точностью восстанавливать неизвестный обобщенный показатель прогнозируемой альтернативы объекта в условиях малого числа наблюдений.