9. Методы выявления «сезонной» составляющей в рядах динамики

Уровни ряда динамики формируются под влиянием взаимодействия многих факторов, одни из которых, будучи основными, главными, определяют закономерность, тенденцию развития, другие, случайные, вызывают колебания уровней.

Как ранее отмечалось, динамика ряда включает три компоненты:

• долговременное движение (так называемый тренд);

• кратковременное систематическое движение (например, сезонные колебания);

• несистематическое случайное движение, вызывающее колебания уровней относительного тренда.

Изучая ряды динамики, исследователи пытаются разделить эти компоненты и выявить основную закономерность развития явления в отдельные периоды, то есть выявить общую тенденцию в изменении уровней рядов, освобожденную от действия случайных факторов. С этой целью (устранить колебания, вызванные случайными причинами) ряды динамики подвергают обработке.

Существует несколько методов обработки рядов динамики, помогающих выявить основную тенденцию изменений уровня ряда, а именно: метод укрепления интервалов, метод скользящей средней и аналитическое выравнивание. Во всех методах вместо фактических уровней при обработке ряда рассчитываются иные (расчетные) уровни, в которых тем или иным способом взаимопогашается действие случайных факторов и тем самым уменьшается колеблемость уровней. Последние в результате становятся как бы «выровненными», «сглаженными» по отношению к исходным фактическим данным. Такие методы обработки рядов называются сглаживанием, или выравниванием, рядов динамики.

9.1. Выравнивание рядом Фурье

Особое место в аналитическом выравнивании динамических рядов занимает выравнивание с помощью ряда Фурье, в котором уровни можно выразить как функцию времени следующим уравнением:

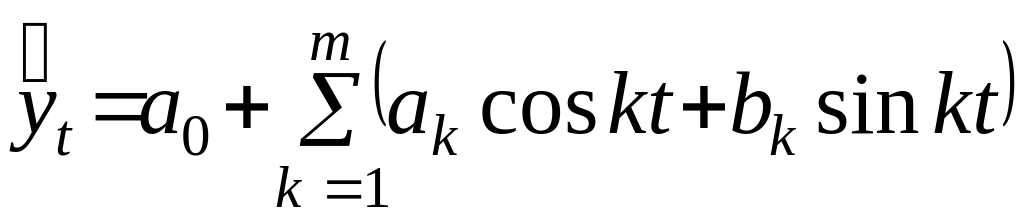. (9.1)

Выравнивание по формуле (9.1) рекомендуется проводить в тех случаях, когда в эмпирическом ряду наблюдается периодичность изменений уровней. В этом случае периодические колебания уровней динамического ряда можно представить в виде синусоидальных колебаний. Поскольку последние представляют собой гармонические колебания, то синусоиды, полученные при выравнивании по ряду Фурье, называют гармониками различных порядков. Показатель k в уравнении (9.1) определяет число гармоник. Обычно при выравнивании по ряду Фурье рассчитывают несколько гармоник (чаще не более 4) и затем уже определяют, с каким числом гармоник ряд Фурье наилучшим образом отражает изменения уровней ряда.

При выравнивании по ряду Фурье периодические колебания уровней динамического ряда представлены в виде суммы нескольких синусоид (гармоник), наложенных друг на друга.

Так, например, при k=1 ряд Фурье будет иметь вид

а при k=2 соответственно

.

Параметры уравнения теоретических уровней, определяемого рядом Фурье, находят, как и в других случаях, методом наименьших квадратов. Приведём без вывода формулы, используемые для исчисления параметров ряда Фурье:

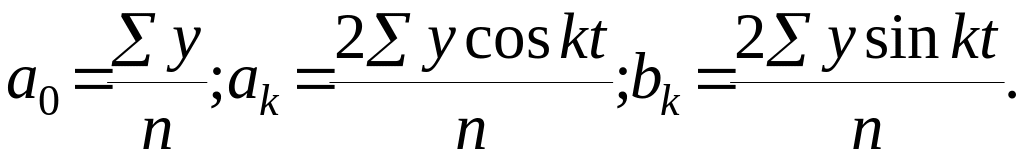(9.2)

Последовательные значения t обычно определяются от 0 с увеличением (приростом), равным – , где п – число уровней эмпирического ряда.

Например, при п=10 временные точки t можно записать следующим образом:

или (после сокращения)

При n=12 значения t, соответственно, будут

.

Значения sin kt и cos kt удобно расположить в таблице. Например, в табл. 9.1, приведены значения sin kt и cos kt (k=1 k=2) для п=12.

Выравнивание по ряду Фурье часто даёт хорошие результаты в рядах, содержащих сезонную волну.

Проиллюстрируем выражение по ряду Фурье на условном примере данных о продаже зимней одежды в одном из районов города в отчетном году.

Таблица 9.1. Значения коэффициентов в разложении (9.1) для п=12

t	cos t	cos 2t	sin t	sin 2t
0 π/6 π/3 π/2 2π/3 5π/6 π 7π/6 4π/3 3π/2 5π/3 11π/6	1 0.866 0.5 0 -0.5 -0.866 -1 -0.866 -0.5 0 0.5 0.866	1 0.5 -0.5 -1 -0.5 0.5 1 0.5 -0.5 -1 -0.5 0.5	0 0.5 0.866 1 0.866 0.5 0 -0.5 -0.866 -1 -0.866 -0.5	0 0.866 0.866 0 -0.866 -0.866 0 0.866 0.866 0 -0.866 -0.866

Таблица 9.2. Сводная таблица расчётных разложений

Месяц	t	Продано, тыс. руб. y	y cos t	y sin t		y cos 2t	y sin 2t
1 2 3 4 5 6 7 8 9 10 11 12	0 π/6 π/3 π/2 2π/3 5π/6 π 7π/6 4π/3 3π/2 5π/3 11π/6	37 40 44 52 46 70 60 48 46 38 36 35	37.0 34.64 22.0 0 -23.0 -60.62 -60.0 -41.57 -23.0 0 18.0 30.31	0 20.0 38.1 52.0 39.84 35.0 0 -24.0 -39.84 -38.0 -31.17 -17.5	35 39.3 45.5 51.7 56.5 58.4 57.0 52.7 46.5 39.3 35.5 33.6	37 20 -22 -52 -23 35 60 24 -23 -38 -18 17.5	0 34.64 38.1 0 -39.84 -60.6 0 41.57 39.84 0 -31.18 -30.31	37.9 39.6 43.0 43.8 56.2 61.0 59.9 53.0 44.0 36.4 35.2 36.2
n=12		552	-66.24	34.43	551.0	17.5	-7.78	551.2

В табл. 9.2 приведены исходные и расчеты показателей, необходимых для получения уравнения первой гармоники (k=1). Итак,

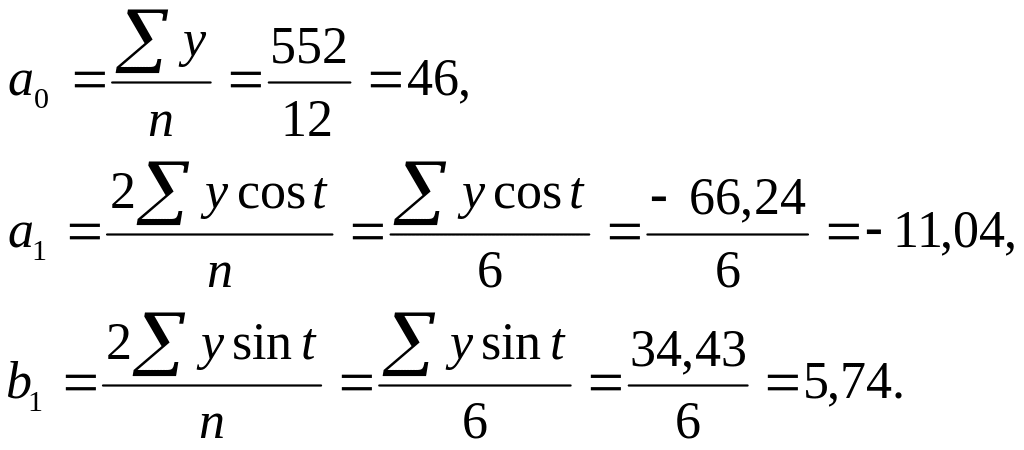
Отсюда

.

Подставляя в данное уравнение значения cos t и sin t (из табл. 9.1), получаем теоретические значения объема продажи по месяцам, показанные в графе «у_t» табл. 9.2. Как видно, теоретические значения y_t, рассчитанные по уравнению первой гармоники, заметно отличаются от эмпирических у. Поэтому попытаемся определить уравнение второй гармоники, то есть

Необходимые расчеты также приведены в табл. 9.2.

Находим параметры а₂ и b₂:

Отсюда уравнение второй гармоники

Подставляя в данное уравнение значения cos t, sin t, cos 2t, sin 2t (из табл. 9.1), получаем теоретические значения (см. последнюю графу табл. 9.2).

Нетрудно заметить, что теоретические значения , рассчитанные по уравнению второй гармоники, более близки к эмпирическим уровням, чем . Об этом свидетельствует и сумма квадратов отклонений теоретических значений от эмпирических:

Аналогично рассчитывают параметры уравнения с применением третьей и четвертой гармоник и проверяют близость теоретических значений к эмпирическим.

В заключение отметим, что выравнивание играет важную роль в анализе рядов динамики. Правильный подбор типа кривой для определения тренда представляет не только теоретический, но и практический интерес, в частности при прогнозировании.

Следует отметить, что найденные уравнения тренда часто используют для прогнозирования методом экстраполяции, то есть распространения в будущее закономерности развития, выявленной в прошлом, в исследованном периоде. Однако экстраполировать ряд по уравнению тренда можно только тогда, когда есть уверенность в том, что выявленная и описанная уравнением тренда закономерность развития устойчива и сохранится и будущем, то есть что условия, в которых происходили изучаемые явления в определенном периоде и в прошлом, стабильны и предположительно не изменятся и в ближайшем будущем, на которое экстраполируется ряд.