31. Приближенные способы преобразования случайных чисел. [1/2]

1. Универсальные способы, которые пригодны для получения чисел с любым законом распределения.

2. Неуниверсальные способы, которые пригодны для получения чисел с конкретным законом распределения.

Неуниверсальный способ:

Пример. Получить случайные числа, имеющие закон распределения Пуассона: . Воспользуемся т. Пуассона:

Если p – вероятность наступления события A, то вероятность наступления m событий в N независимых испытаниях при ,,, асимптотически равноp(m).

Выберем N испытаний такими, чтобы . Будем проводить серии изN независимых испытаний, в каждом из которых события A наступает с вероятностью p. Будем подсчитывать число случаев y_i фактического наступления события A серии с номером j. Числа y_i будут следовать закону распределения Пуассона. N выбирают таким, чтобы p=0.1÷0.2.

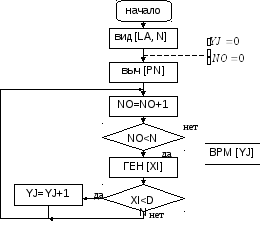
Схема моделирующего алгоритма:

NO – вспомогательная переменная

51

Универсальный способ основан на кусочной аппроксимации функции плотности.

П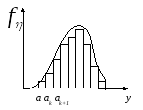усть требуется получить последовательность случайных чисел {y_j}, с заданной функцией плотности , значения которой лежат в интервале (a, b).

Представим функцию плотности в виде кусочно-постоянной функции. Для этого разобьем интервал (а,b) на m интервалов, на каждом из которых , тогда случайную величину можно представить.

- случайная величина, равномерно распределенная в интервале (a_k, a_k+1).

Целесообразно разбить интервал (a, b) на интервалы таким образом, чтобы вероятность попадания величины в интервал (a_k, a_k+1) не зависело от номера интервала. Тогда:

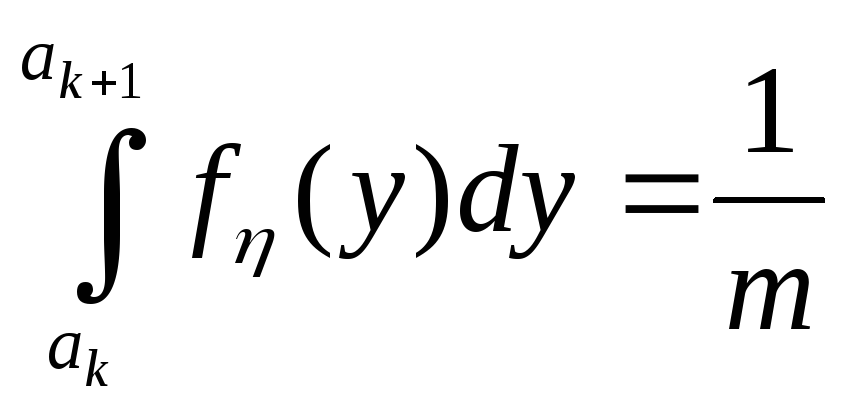
Алгоритм машинной реализации:

1) Генерируются случайное число x_i из интервала (0, 1)

2) С помощью этого числа случайным образом выбирается интервал (a_k, a_k+1).

3) Генерируется x_i+1 и домножается на коэффициент масштабирования (a_k+1 - a_k).

4) Вычисляется число y_j=a_k+x_i+1(a_k+1 - a_k).

Достоинства: небольшие затраты машинного времени, так как операция масштабирования выполняется 1 раз перед моделированием.

52

32. Моделирование непрерывных случайных векторов. [1/1]

Двумерная случайная величина в этом случае описывается совместной функцией плотности f(x, y) с двумя составляющими .f(x, y) позволяет определить :. Отсюда можно определитьx_i. Можно также определить . Отсюда определяемy_i.

(x_i, y_i) – первая реализация непрерывного случайного вектора. Этот способ может применяться для векторов с размерностью >2, однако, с ростом n, значительно увеличивается число вычислений. При n>2 формирование случайных векторов выполняется с использованием корелляционной теории.

53

33. Моделирование дискретных случайных векторов

Когда случайный вектор расположен на плоскости XOY, он может быть задан совместным законом распределения его проекций на осиOx и Oy. Рассмотрим дискретный случайный процесс: двумерная случайная величина является дискретной, и ее составляющаяпринимает значенияx₁, x₂, …, x_n, а . Тогда каждой паре (x_i, y_i) соответствует вероятность p_ij. Каждому возможному значению x_i соответствует вероятность (1). В соответствии с распределением вероятностей (1) можно определить конкретное значениеx_i1, и из всех значений p_ij можно выбрать последовательность p_i11, p_i12, …, p_i1n (2). Распределение (2) описывает условное распределение величины , при условии, что. Определяется конкретное значениеy_i1. Пара (x_i1, y_i1) является первой реализацией дискретного случайного вектора. Далее, аналогично определяется возможное значение x_i2, распределение p_i21, p_i22, …, p_i2n (3) => находят y_i2. И т. д.

54