1.1.3. Теплопроводностные механизмы отвода тепла. Уравнение теплопроводности, начальное и граничные условия

Перенос тепловой энергии (кинетической энергии микрочастиц) в веществе определяется процессами теплопроводности. Явление теплопроводности проявляется при непосредственном соприкосновении отдельных частиц тела или отдельных тел, имеющих различные температуры. В газах перенос тепловой энергии осуществляется путем взаимодействия диффундирующих молекул и атомов, а в жидкостях и твердых телах (диэлектриках) – упругих волн (фононов). В проводниках перенос энергии в основном осуществляется путем диффузии свободных электронов.

Процесс переноса теплоты теплопроводностью возможен лишь тогда, когда в различных точках тела температура неодинакова. Поэтому передача теплоты теплопроводностью в веществе сопровождается изменением температуры, как в пространстве, так и во времени.

Температурным полем называют совокупность значений температуры во всех точках рассматриваемого тела, положение которых задано координатами , , или вектором , в каждый фиксированный момент времени . Основной задачей теории теплопроводности является изучение пространственно-временного распределения температуры, то есть определение зависимости .

Температурное поле, изменяющееся как в пространстве, так и во времени, называется нестационарным температурным полем. Для нестационарного температурного поля характерен неустановившийся режим теплопроводности, когда температура изменяется с течением времени. При обработке материала импульсным лазерным излучением возникает нестационарное температурное поле.

При установившемся тепловом режиме температура в каждой точке тела с течением времени остается неизменной, меняясь лишь от точки к точке. Такое температурное поле называется стационарным. При этом температура является функцией только координат.

, .

В теле с температурой можно выделить поверхность, во всех точках которой в любой, но один и тот же момент времени , температура одинакова. Такая поверхность называется изотермической. Ее уравнение имеет вид

При анализе теплообмена между двумя бесконечно близко расположенными изотермическими поверхностями с температурами и (рис. .2) можно показать, что скорость изменения температуры в некоторой локальной точке пространства в направлении определяется производной функции по направлению

,

, , - направляющие углы вектора в декартовой системе координат.

Наибольшая скорость изменения температуры наблюдается в направлении нормали к изотермической поверхности . Следовательно, в любой точке изотермической поверхности можно построить некоторый вектор, направленный по нормали к этой поверхности в сторону увеличения температуры, который характеризует скорость возрастания температуры в этом направлении (т.е. производную от температурной функции по направлению нормали ). Такой вектор называют градиентом температурного поля и записывают в виде

, , - единичные векторы, совпадающие по направлению с координатными осями соответственно.

Независимо от выбора направления нормали вектор направлен в сторону возрастания температуры. Он показывает насколько интенсивно (резко) меняется температура внутри тела.

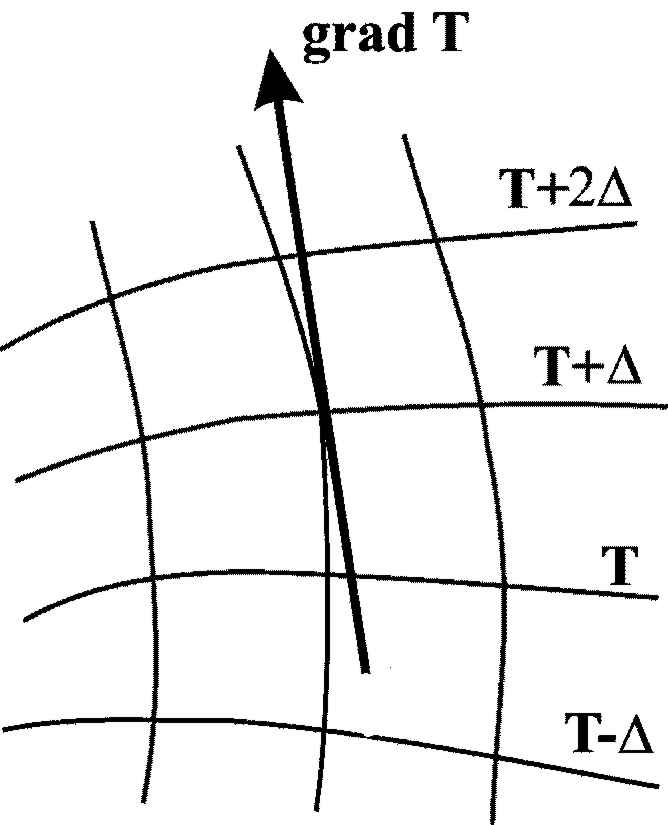
Рис. 1.2. К определению температурного градиента и изотермической поверхности

Согласно сказанному выше, можно записать

,

В теле с неравномерным распределением температуры (не находящемся в полном тепловом равновесии) всегда происходит перенос теплоты, то есть для передачи теплоты теплопроводностью необходимо, чтобы существовал градиент температуры, который определяет величину теплового потока. В этом смысле температурный градиент является основным физическим параметром, определяющим условие возникновения процесса передачи теплоты. Тепловой поток, в отличие от температуры (величины скалярной) имеет вполне определенное направление: от точек тела с высокой температурой к точкам тела с более низкой.

Связь между величинами, определяющими передачу теплоты, устанавливает уравнение теплопроводности. Уравнение теплопроводности выведено на основе закона сохранения энергии и закона Фурье. В общем случае задача теплопроводности описывается системой дифференциальных уравнений. В случае неподвижного источника тепла эта система имеет вид:

(1.1)

Теплофизические коэффициенты – удельная теплоемкость, –плотность, – коэффициент теплопроводности в общем случае зависят от координат, времени и температуры. Плотность мощности теплового источника , действующего в объеме тела, в общем случае также зависит от температуры. Тепловой поток измеряется количеством теплоты, проходящим в единицу времени через единицу площади поверхности, перпендикулярной направлению потока в рассматриваемой точке.

При описании лазерного нагрева вещества необходимо учитывать следующие обстоятельства. Поскольку световая волна проникает в глубь среды, то тепловые источники распределены в объеме среды, они являются объемными, то есть. Из-за уменьшения интенсивности лазерного излучения по мере проникновения его в глубь материала выделение энергии происходит неоднородно по объему взаимодействия, что приводит к неоднородному нагреву вещества и, как следствие, вызывает в нем интенсивные процессы тепло- и массопереноса между различными участками.

Наиболее удобна для аналитического анализа ситуация, когда материал, облучаемый лазерным пучком:

а) изотропен и гомогенен, то есть свойства его одинаковы по всем направлениям, а температурные зависимости оптических и теплофизических коэффициентов слабые.

б) объемный источник теплоты не зависит от температуры.

В этом случае, так как ( – оператор Лапласа), систему (.1) можно преобразовать к следующему уравнению теплопроводности

(1.2)

где – коэффициент температуропроводности.

Уравнению (.2) должна удовлетворять функция , представляющая собой распределение температуры в теле.

В отличие от теплопроводности , которая характеризует способность материала проводить тепло, температуропроводность характеризует теплоинерционные свойства тела. Она является мерой скорости выравнивания температурного поля в рассматриваемой среде. Чем больше , тем быстрее меняется во времени температура. То есть характеризует способность вещества изменять с большей или меньшей скоростью свою температуру во времени (определяет эффективность разогрева среды в процессе переноса тепла).

Особо важно подчеркнуть, что вид решения уравнения (.2) определяется функцией, зависимой от плотности тепловых источников и значениями теплофизических постоянных , , а однозначность решения – граничными условиями для каждой конкретной задачи нагрева. В частности, значение определяет максимальную температуру, соответствующую данной плотности мощности объемных тепловых источников .

При нагревании твердых тел лазерным излучением распределение плотности мощности светового потока в поглощающей среде по глубине описывается законом Бугера – Ламберта, который при коэффициенте поглощения зависящем только от глубины ( ) имеет вид:

, (1.3)

где – плотность падающего светового потока на поверхность материала, – поглощательная способность материала. Поэтому, согласно (.3), плотность мощности объемных тепловых источников может быть определена как

(1.4)

В материале с малой теплопроводностью при определенной равновесная температура всегда выше, чем в веществе с большим значением . Удельная теплоемкость проявляется в способности материала накапливать тепло, поступающее от внешнего источника, пока не достигнуто состояние равновесия. Коэффициент же температуропроводности определяет, как уже было отмечено, скорость установления теплового равновесия в материале при мгновенном включении теплового источника. При этом расстояние, на которое тепловая волна проникает в глубь материала за время , может быть оценено как . Размер прогретой области материала растет за счет температуропроводности пропорционально этому параметру.

Уравнение (.2) получено при некоторой идеализации процесса, поэтому оно является феноменологическим (описательным) уравнением. Вопрос о том, насколько точно это уравнение описывает реальный физический процесс, происходящий при взаимодействии лазерного излучения с материалами, может быть решен только сравнением результатов, полученных при решении уравнения и в эксперименте. В абсолютном большинстве случаев феноменологическое описание процесса теплопроводности находится в весьма удовлетворительном согласии с экспериментом, конечно, при правильном выборе модели реального процесса.

Уравнение теплопроводности есть дифференциальное уравнение в частных производных, в котором независимыми переменными являются время и три пространственные координаты, а зависимой переменной – функция (температура). Это уравнение первой степени (линейное), поскольку зависимая переменная входит в него только в первой степени. Но вместе с тем, оно является уравнением второго порядка, так как оператор Лапласа содержит производные второго порядка от температуры по пространственным координатам. Функция (в общем случае) считается заданной функцией координат и времени.

Уравнение теплопроводности является математической моделью целого класса процессов теплопроводности, но оно само по себе ничего не говорит о развитии процесса передачи теплоты от лазерного источника в рассматриваемом теле. Математически это объясняется неоднозначностью решения дифференциальных уравнений в частных производных. Чтобы получить частное решение, соответствующее конкретной задаче нагрева материала, необходимо иметь дополнительные данные, которых нет в дифференциальном уравнении теплопроводности. Эти дополнительные условия, которые однозначно определяют конкретную задачу теплопроводности, называются условиями однозначности. В условия однозначности входят:

1) геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс теплообмена;

2) условия, определяющие физические и теплофизические свойства тела (тепло- и температуропроводность, теплоемкость, плотность), а также закон распределения объемных источников теплоты ;

3) граничные условия, характеризующие особенности теплового взаимодействия граничной поверхности тела с окружающей средой. В частности, необходимо знать, каким образом происходят потери тепла с поверхности: либо с помощью лучеиспускания (по закону Стефана - Больцмана), конвекции (по закону Ньютона) или испарения;

4) временные или начальные условия, определяющие распределение температуры в любой точке тела в некоторый момент времени, который для конкретной физической задачи задается или принимается за нулевой .

Для тела определенной геометрической формы с известными физическими свойствами (заданы , , , ) условия однозначности сводятся к заданию начального и граничных условий. Начальное условие является краевым условием по времени, а граничные условия – пространственным краевым условием. Эти условия в совокупности называются краевыми условиями. Дифференциальное уравнение теплопроводности вместе с краевыми условиями составляет краевую тепловую задачу.

Начальное условие для уравнения теплопроводности обычно состоит в задании температуры в начальный момент времени во всех точках обрабатываемой лазерным излучением детали

, . (1.5)

Граничные условия – условия теплового взаимодействия тела с окружающей средой – могут быть заданы в различной форме в зависимости от характера процесса. В тех случаях, когда на границе тела не происходит никаких процессов с поглощением или выделением теплоты, а теплообмен определяется только теплопроводностью, граничные условия на поверхности заключаются в равенстве температуры и тепловых потоков на границе

, , (1.6)

где и – температуры тела и среды, и – теплопроводности тела и среды, – нормаль к граничной поверхности тело – среда, - производная по направлению нормали к граничной поверхности.

Условие (.6) весьма неудобно, так как для расчета температуры материала необходимо отыскивать температуру и в окружающей среде, обычно это воздух или газы, подаваемые в зону обработки. По этой причине в большинстве практических случаях используют условия, представляющие собой некую идеализацию действительных физических процессов.

Граничное условие I рода состоит в задании распределения температуры на поверхности тела для любого момента времени

. (1.7)

В частном случае, когда температура на поверхности постоянна на протяжении всего времени протекания процессов теплообмена, условие (.7) упрощается и принимает вид .

При граничных условиях II рода задаются значения плотности теплового потока для каждой точки поверхности тела как функции координат и времени

(1.8)

– нормаль к поверхности, – поглощательная способность материала, – функция, описывающая временную структуру и пространственное распределение плотности потока излучения по поверхности тела, – плотность мощности тепловых потерь, связанных с радиационным или конвективным теплообменом. В случае, когда , потерями тепла с поверхности можно пренебречь. При лазерной обработке указанное условие обычно справедливо при таких плотностях мощности лазерного излучения и временах облучения, когда температура поверхности не превышает температуру плавления.

Именно краевые тепловые задачи с граничными условиями II рода представляют наибольший интерес для процессов взаимодействия лазерного излучения с материалами.

Если заданы температура окружающей среды и закон теплообмена между окружающей средой и поверхностью обрабатываемого материала, то говорят, что в тепловой задаче заданы граничные условия III рода

(1.9)

где – коэффициент теплопередачи ( = Вт/(м²К)) характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Условие (.9) можно с учетом закона Фурье представить в виде

(1.10)

где – нормаль к поверхности тела: индекс " " указывает, что значение температуры и градиента определяются на поверхности тела.

Уравнение (.10) по существу является частным выражением закона сохранения энергии для поверхности тела.

Напомним, что решение уравнения (.3) может быть получено несколькими способами. Наиболее математически мощными и универсальными являются метод разделения переменных, операционный метод или метод интегральных преобразований и метод источников или метод функций Грина.

Операционный метод является одним из самых эффективных аналитических методов при решении краевых задач теплопроводности. Причем решения, получаемые операционным методом, удобны для практического использования. Операционный метод основан на преобразовании искомой функции по одной из переменных, причем это преобразование выбирается с таким расчетом, чтобы уравнение для новой (преобразованной) функции было значительно проще исходного. Находят решение преобразованного уравнения, а затем, применяя к нему обратное преобразование, определяют решение исходного уравнения.

В качестве преобразования, позволяющего реализовать эту идею, обычно применяют преобразования Лапласа по времени.

, (1.11)

где - действительное переменное, - комплексный параметр.

Функция в (.11) называется оригиналом, а - изображением .

Широкое применение операционного метода основано на том, что дифференцированию функции в пространстве оригиналов соответствует алгебраическая операция умножения в пространстве изображений . Благодаря этому свойству преобразование Лапласа является одним из основных методов решения дифференциальных уравнений в частных производных, в том числе уравнения теплопроводности. Использование преобразования Лапласа позволяет уменьшить на единицу количество переменных, по которым производится дифференцирование. В частности, если в уравнении теплопроводности есть производные по времени и одной координате, то в пространстве изображений в соответствующем уравнении будет только производная по одной координате, т.е. уравнение теплопроводности будет обыкновенным дифференциальным уравнением.

Другим мощным математическим методом аналитического решения краевых задач теплопроводности типа (.3) является метод источников или функций Грина. Метод функции Грина весьма универсален: его можно применять для решения краевых задач при достаточно общей постановке в одно, двух и трехмерных случаях, ограниченных и неограниченных областях, при однородных и неоднородных, начальных и граничных условиях, причем как для нестационарных, так и для стационарных температурных полей.

Идея метода состоит в том, что сначала находят специальное решение краевой задачи теплопроводности того же типа (так называемую функцию Грина ), но более простое. Через него определяют интегральное представление решения исходной задачи.

Важным является понятие источника теплоты, локализованного в точке пространства и имеющего вид "мгновенного" теплового импульса, т.е. источника вида

- дельта-функция, , .

При этом, решение уравнения теплопроводности можно заменить решением уравнения относительно функции Грина

Если в уравнении (.2) нет объемных тепловых источников = 0, то для одномерного случая функция вида

(1.12)

удовлетворяет уравнению теплопроводности и называется фундаментальным решением уравнения теплопроводности.

Начальное распределение температуры, удовлетворяющее условию (.12) называется тепловым импульсом. С учетом этого понятия можно сказать, что фундаментальное решение уравнения теплопроводности (.2) дает распределение температуры в любой точке облучаемого тела в момент времени , которое вызывается мгновенным точечным источником теплоты , действующим в точке в момент времени .

Из рис. .3 следует, что во всякой точке тела температура, создаваемая мгновенным точечным источником тепла, действующим в точке , при определяется фундаментальным решением уравнения и довольно быстро выравнивается.

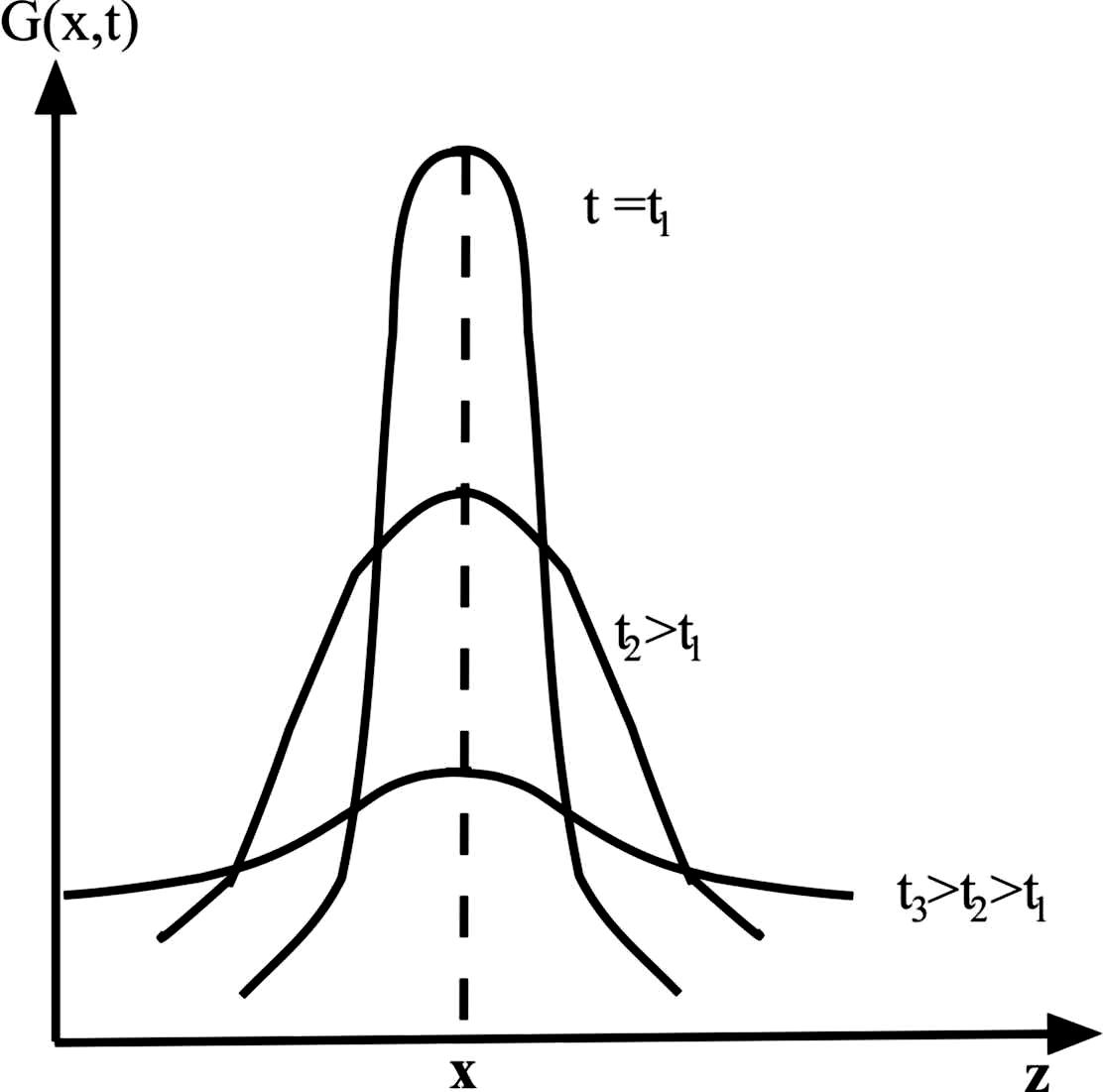
Рис. 1.3. Графическое представление фундаментального решения уравнения теплопроводности

Из сказанного следует, что функция Грина описывает влияния мгновенного точечного теплового источника на температурное поле. Вследствие линейности уравнения теплопроводности вместе с граничными и начальными условиями, решение краевой задачи теплопроводности имеет вид:

(1.13)

Зная начальное распределение температуры и фундаментальное решение (функцию Грина) можно установить искомое температурное поле (в одномерном случае):

(1.14)

Согласно решению (.13, .14), после мгновенного точечного теплового импульса температура в точке нагрева убывает с течением времени по закону , а характерный размер зоны термического влияния растет .

Метод источников (функция Грина) успешно используется при решении тепловых задач лазерного воздействия на материалы с низкой температуропроводностью (биологические объекты, неметаллы и т.д.), в этом случае мгновенный тепловой источник действительно локализован, поэтому можно установить характерные закономерности изменения температурного поля в объеме материала.