1.3. Линейные режимы лазерного нагрева.

Дифференциальное уравнение теплопроводности определяет временное и пространственное распределение температуры внутри нагреваемого тела в любой момент времени. Для того чтобы найти температурное поле, надо знать распределение температуры внутри тела в начальный момент времени (начальные условия), геометрическую форму и размеры тела, закон теплового взаимодействия между поверхностью тела и окружающей средой (граничные условия).

В реальных условиях чаще всего параметры процесса нагревания веществ лазерным излучением зависят от температуры и, следовательно, от пространственного ее распределения. Аналитически решить реальные задачи чаще всего не удается.

Получить аналитическое выражение для распределения температурного поля возможно, когда материал, облучаемый лазерным пучком изотропен и гомогенен, а температурные зависимости оптических и теплофизических коэффициентов являются слабыми, и, кроме того, источник теплоты не зависит от температуры. Это, так называемые, линейные режимы лазерного нагрева.

Действительно, температурная зависимость теплофизических и оптических постоянных для многих материалов не слишком резкая, поэтому при постановке задач нагрева (в первом приближении) эту зависимость можно не учитывать. Поглощательная способность и коэффициент отражения зависят от длины волны лазерного излучения и плотности потока излучения. Однако даже при относительно невысоких потоках (< 10⁶ Вт/см²) их величина известна с небольшой точностью. С ростом температуры коэффициент поглощения a может изменяться. Поэтому в большинстве случаев полагают, что поглощательная способность не зависит от температуры, и в оценках используют ее среднее значение по некоторому интервалу температур.

1.3.1. Нагрев полупространства экспоненциально спадающим с глубиной тепловым источником.

Лазерный нагрев по своей физической сущности не отличается от других видов теплового воздействия, поскольку основная доля теплоты при лазерном воздействии переносится в глубь металла посредством электронной проводимости. Это дает основание рассматривать задачи лазерного нагрева в рамках классической теории теплопроводности. Главная задача при этом состоит в адекватном описании теплового источника в месте воздействия лазерного излучения.

Для получения качественных представлений о нагреве материала непрерывным лазерным излучением достаточно моделировать временный ход оптического воздействия ступенчатой функцией Хевисайда:

В качестве примера установления граничных условий для краевой задачи теплопроводности рассмотрим процесс выравнивания электронной и решеточной температур при лазерном нагреве металла рис. (.14).

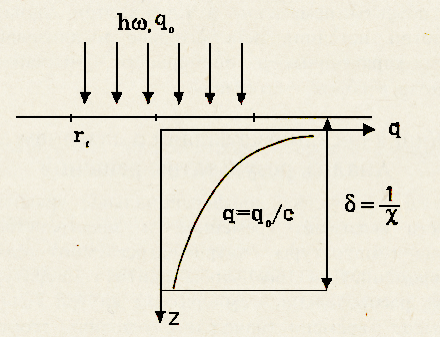
Рис. 1.14. К постановке краевой задачи теплопроводности при выравнивании температур и

Предположим, что на металл, поглощательная способность которого не зависит от температуры, падает лазерное излучение, плотность потока которого равномерно распределена по пятну нагрева радиуса

и не зависит от времени.

Выявление основных закономерностей процесса удобно проводить для одномерных моделей, применение которых справедливо при , где – коэффициент температуропроводности. Практически все начальные стадии нагрева металлов как импульсным, так и непрерывным излучением можно рассматривать в одномерном приближении. В одномерном приближении металл можно представить полупространством, т.е. .

Поскольку закон Ома выполняется в области частот видимого и ИК-спектра, то тепловое действие световой волны первоначально проявится в ограниченном поверхностном слое (скин-слое), так как поле затухает в металле экспоненциально

,

при этом толщина скин-слоя равна

( – плазменная частота).

Свет в металлах поглощается главным образом свободными электронами. Электронный газ и решетка в металле  две слабо взаимодействующие подсистемы. При выполнении условий

(1.33)

( - время установления равновесного распределения по энергиям в электронном газе) и

(1.34)

(  частота столкновений ион-ион;  частота электронно-ионных столкновений) электронный газ и решетку можно характеризовать в отдельности электронной и решеточной температурами. Выполнение условия (.33) означает быстрое перераспределение поглощенной энергии между электронами проводимости, а (.34) означает, что энергия, передаваемая решетке электронами, быстро перераспределяется между ионами.

Рассмотрим последовательно частоты релаксаций , , , , соотношения между которыми существенно определяют характер процессов в металлах при поглощении излучения.

Частота столкновений электронов с фотонами пропорциональна плотности мощности лазерного излучения, поглощенного металлом . Она может быть оценена с помощью соотношения

(1.35)

 поверхностная плотность мощности [эрг/см²с];  энергия кванта [эрг]; n  концентрация электронов, поглощающих излучение [см^3].

Для видимого участка спектра, , (  температура электронов ~ 10³ К). Тогда (n ~ 510²² см^3  концентрация электронов проводимости;  энергия Ферми);

,

где  постоянная Планка;  масса электрона;  5  10 эВ.

Частота межэлектронных столкновений в металле преимущественно определяется количеством электронов в области размытости Ферми и вычисляется с помощью соотношения

, (1.36)

где  скорость электрона на поверхности Ферми ~ 10⁸ см/с;  сечение взаимодействия электрон  электрон; 510^16 см²;  область размытости Ферми. Тогда при ~ 10³ К величина  10¹⁴ с^1, а время установления равновесного распределения электронного газа ~ 10^14с. Скорость передачи энергии электронного газа решетке и температура определяются источником тепла и коэффициентом теплоотдачи от электронов решетке.

Количество энергии, получаемое решеткой от электронного газа в единице объема в единицу времени равно

~10¹⁰ Вт/(см³град) - коэффициент теплообмена между электронами и решеткой.

Частота электронно-ионной релаксации может быть выражена через коэффициент теплообмена

,

где  объемная теплоемкость решетки [10^7 Втс/(см³град)]. Подстановка численных значений дает 10¹¹ с^1 и 10^11 с.

Сравнивая равенства (.35) и (.36), можно показать, что при плотностях потока излучения 10⁹ Вт/см² условие (.33) выполняется всегда и электронный газ в металле характеризуется температурой . Аналогично выполняется условие (.34), поэтому для описания теплового состояния решетки можно ввести температуру .

С учетом вышеприведенных замечаний получим следующие уравнения теплопроводности для электронной

(1.37)

и решеточной температуры

, (1.38)

где – проникающий тепловой поток, который затухает по экспоненциальному закону; – коэффициент теплообмена между электронной и решеточной подсистемами; , – соответственно теплоемкости кристаллической решетки и электронного газа; , – коэффициенты теплопроводности для рассматриваемых подсистем; – определяет энергию, получаемую решеткой от электронного газа в единице объема в единицу времени, т.е. имеет физический смысл теплового источника для решетки.

Граничные условия запишем в следующем виде (граничные условия II рода)

,

т.е. поверхность теплоизолирована от окружающей среды, практически это выполняется для Вт/м² всегда. Начальные и конечные условия стандартны

, .

На начальном этапе облучения передача энергии решетке отсутствует, поэтому электронный газ греется изолированно и очень быстро из-за его небольшой теплоемкости . Температура решетки изменяется мало, поскольку время релаксации температуры электронного газа существенно меньше времени релаксации температуры решетки. Затем рост температуры замедляется из-за того, что становится существенной теплопередача решетке, начинается ее разогрев. Таким образом, с определенного момента времени электронный газ является буферным, передаточным звеном, эффективность которого максимальна тогда, когда максимальна. В дальнейшем эта разность (см. рис. .15) уменьшается и можно ввести понятие температуры металла. Обычно это время выравнивания 10^-9 с.

Поскольку и , то можно пренебречь первым членом в уравнении (.37) и вторым членом в (.38), получим:

(1.39)

. (1.40)

Перепишем (.39), (.40) в удобном для анализа виде, вводя табличные параметры процесса теплопередачи и металле, а именно положив , , где и - соответственно истинные (табличные) коэффициент теплопроводности и теплоемкость металла,

(1.41)

, (1.42)

–время начала роста температуры решетки.

Проанализируем частные случаи решения системы (.41, .42).

Решение зависит от трех характерных масштабов , , : – глубина затухания световой волны (толщина скин-слоя); – параметр, характеризующий разогрев электронного газа и энерговыделение в решетке; – глубина проникновения теплового потока в глубь материала из-за теплопроводности.

1) При ( см, см) решение системы (.41, .42) имеет вид:

,

где и – функции Бесселя нулевого и первого порядков, , . Температура определяет перегрев электронного газа по отношению к температуре решетки.

Оценим перегревы, которые могут быть при Вт/см², 1 Вт/см К, 0,1.

К.

Это очень высокая степень перегрева. Из рис. .15 следует, что, начиная с некоторого времени , рост за счет обмена энергией электронного газа с решеткой существенно быстрее, чем рост , поэтому через определенное время можно ввести понятие температуры металла . Это произойдет при времени , когда , с. Таким образом, при длительности лазерного импульса с можно с хорошим приближением считать, что , те есть идет уже прогрев металла как единого целого. При этом оптические свойства не должны зависеть от температуры ( ).

Рис. 1.15. Схема изменения решеточной и электронной температур от времени.

2) , – это случай, когда тепловой поток мгновенно разогревает решетку, разрыва в величинах и нет, весь процесс поглощения энергии лазерного импульса определяется глубиной проникновения световой волны в толщину металла, т.е. определяется коэффициентом поглощения в законе Бугера - Ламберта (.3). Решением системы (.41, .42) будет

где – функция Лапласа или интеграл ошибок.

В аналитической теории теплопроводности широко применяется интеграл типа

,

который называется функцией Лапласа или интегралом ошибок. Значения этой функции табулированы. Установлено, что

а) монотонно возрастает, изменяясь в пределах -1,+1, и , так что таблицы составлены только для положительных значений аргумента:

б) , , , .

В некоторой литературе используют обозначения , а также , .

При ,

- дополнительная функция ошибок.

При , для

В частности , при .

Выпишем в заключение формулу для перегрева электронного газа в общем случае:

Используя ее можно получить оба рассмотренных частных случая.

Теперь рассмотрим задачу о нагревании полупространства равномерно распределенным по его поверхности лазерным излучением с плотностью мощности , объемный источник тепла будет ( ). Считаем, что с, то есть .

(1.43)

Начальное условие (.5) запишем для равномерного распределения температуры в теле: (в большинстве случаев можно считать ). Тогда, когда процесс нагревания определяется абсолютной температурой, считать нельзя, если процесс реагирует на перепад температуры, то можно принять .

Граничные условия (.7) описывают поведение температуры на большом удалении от облучаемой поверхности

(1.44)

На облучаемой поверхности действуют граничные условия II рода (.8) при

- теплопотери (отрицательные по величине), первый член – потери конвекционные, при 1000 К ~10 Вт/см², второй член – лучистые потери, при 1000 К ~5 Вт/см², последний член – потери на испарение, наиболее существенный, в определенных условиях могут компенсировать ввод тепла полностью.

На стадии, когда разрушения вещества нет (скорость испарения мала), этим членом пренебрегают.

Таким образом, в большинстве случаев поверхность, на которую падает лазерное излучение, можно считать теплоизолированной. Поэтому граничные условия на поверхности выглядят так:

следовательно, при малых потерях

. (1.45)

Применив преобразования Лапласа (.11) к уравнению (.43) и граничным условиям (.44, .45), получим дифференциальное уравнение в полных дифференциалах для рассматриваемой краевой задачи

(1.46)

В (.46) учтено, что , кроме того, и . Условия (.44, .45) приобретают вид:

, .

При этих условиях решение (.46) будет:

Воспользовавшись таблицами обратных преобразований, получим:

(1.47)

- глубина проникновения излучения (масштаб затухания излучения в раз).

Весь разогрев определяется соотношением трех величин, имеющих размерность длины: - координата, - глубина проникновения излучения, - длина теплопроводности (то есть расстояние, на которое уходит температурная волна от места, в котором она образовалась).

Проанализируем выражение (.47). При получим выражение для температуры на поверхности:

(1.48)

Для нахождения температуры на поверхности после окончания воздействия длительностью можно воспользоваться понятием стока. Под стоком понимают источник тепла с отрицательной интенсивностью, равной интенсивности источника, включенный на время позднее источника.

Частные случаи:

1) Теплопроводность еще не работает – , ( ),

(1.49)

весь разогрев определяется тепловыделением на глубине .

Если тепловой поток является функцией времени, то следует заменить на . Для металлов это приближение справедливо при временах . При этих временах для металлов можно говорить только о температуре электронов . Для диэлектриков, когда может быть , выражение (.49) справедливо почти всегда.

В тех случаях, когда теплопроводность играет определяющую роль в распределении температуры ( ), что характерно для большинства случаев лазерного воздействия на металлы, распределение температуры можно получить из (.47) при . Но можно специально решить задачу о нагревании полупространства при поглощении лазерного излучения на границе.