19 Экспоненциальный закон распределения.

В различных приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике и т.д. широко применяется экспоненциальное (показательное) распределение.

Время занятости канала связи, время безотказной работы ЭВМ, продолжительность поиска чего–либо – все это экспоненциально распределенные случайные величины.

Неотрицательная величина X называется распределенной по экспоненциальному закону, если ее плотность распределения имеет вид

,

где - параметр экспоненциального распределения.

График плотности распределения изображен на рис. 13.

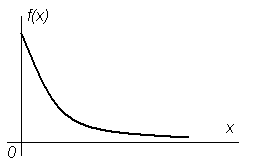
Рисунок 13 График плотности вероятности экспоненциально распределенной случайной величины

Определим основные числовые характеристики этого распределения:

,

т.е. математическое ожидание есть величина обратная параметру закона. Для отыскания дисперсии используем формулу

. Откуда средне – квадратичное отклонение будет равно

.

Вероятность попадания случайной величины на заданный участок, распределенной экспоненциально можно рассчитать, используя формулу

.

20 Вероятность попадания случайной величины на заданный участок.

Пусть случайная величина X распределена равномерно на интервале от a до b, причем плотность вероятности ее известна и равна f(x)=1/(b-a). Требуется определить вероятность попадания ее на участок от c до d (рис.9), т.е. .

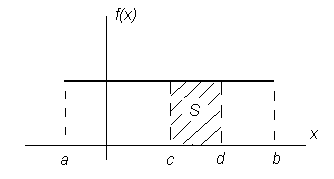
Рисунок 9 Определение вероятности попадания случайной величины на заданный участок

Определяя эту вероятность как интеграл от плотности вероятности f(x), получаем

.

Следовательно, вероятность попадания случайной величины на заданный участок от c до d определяется как площадь заштрихованного прямоугольника.

Округление результатов измерений имеет равномерное распределение.

21 Теорема Чебышева.

При достаточно большом числе независимых опытов среднее арифметическое из опытных данных сходится по вероятности к математическому ожиданию случайной величины.

Пусть a – истинное значение измеряемой величины, - среднее арифметическое ряда измерений, - максимальное значение квадрата отклонения в произведенных измерениях, n – число измерений. Теорема Чебышева утверждает, что

. (5.1)

Для доказательства теоремы обратим внимание на то, что математическое ожидание любого измерения , где a – неизвестное истинное значение измеряемой величины. Далее, так как

, то

, т.е. математическое ожидание среднего значения случайной величины также равно истинному значению a. Дисперсия величины

. Так как можно написать, что

.

Теперь после замены x на и на a легко получаем теорему Чебышева.

Из теоремы следует, что при любых конечных и будет справедливо предельное соотношение

или эквивалентное ему соотношение

.

Таким образом, теорема Чебышева доказывает, что среднее арифметическое опытных данных (измерений) мало отличается от истинного значения при большом числе испытаний. Однако входящее в неравенство значение указывает на то, что увеличением числа измерений нельзя полностью компенсировать ошибки измерительного инструмента.

Выводы теоремы можно распространить и на другие моменты распределения. Например, для дисперсии получаем приближенную формулу, пригодную для практических вычислений:

,

где вместо a, согласно теореме Чебышева, можно пользоваться :

.

Неравенство и теорема Чебышева для практических задач могут использоваться в тех случаях, когда известна дисперсия, очевидно, она должна быть конечной величиной.