36 Условное математическое ожидание. Уравнение линии регрессии.

Определение. Случайные величины являются связанными между собой, если при изменении одной из них другая реагирует изменением своего условного математического ожидания.

Условное математическое ожидание случайной непрерывной величины можно определить по формуле

,

где M(X/Y) - условное математическое ожидание случайной величины X при условии, что случайная величина Y приняла частное значение y.

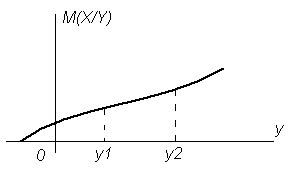
Рисунок 3.9 Графическая интерпретация условного математического ожидания M(X/Y)

Условное математическое ожидание M(X/Y) является функцией случайной величины Y (рис. 3.9). Если , то случайные величины X и Y считаются связанными. Связанность случайных величин является частным случаем их зависимости.

На практике чаще всего M(X/Y) имеет вид прямой линии, которую называют линией регрессии, описываемой уравнением

.

Положение линии регрессии зависит от величины и знака корреляционного момента (рис. 3.10). Если значение корреляционного момента случайных величин X и Y меньше нуля, то регрессия отрицательная, а если значение корреляционного момента больше нуля, то регрессия положительная. Если значение корреляционного момента равно нулю, то случайные величины X и Y между собой не связаны.

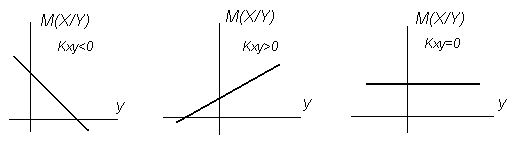
Рисунок 3.10 Положение линии регрессии в зависимости от величины и знака корреляционного момента

37 Корреляционный момент. Коэффициент корреляции.

Для характеристики системы случайных величин важную роль играет второй смешанный центральный момент

,

т.е. математическое ожидание произведения центрированных величин.

Эта характеристика называется корреляционным моментом или ковариацией:

.

Корреляционный момент кроме рассеяния случайных величин X и Y характеризует еще и связь их между собой.

Свойства корреляционного момента:

а) ;

б) ;

в) - корреляционная матрица.

Для системы двух случайных величин числовыми характеристиками являются: .

Из определения корреляционного момента следует, что размерность его равна размерности произведения случайных величин X и Y. Поэтому для одних и тех же величин значения его будут зависеть от единиц измерения случайных величин.

Эта особенность корреляционного момента является его недостатком, так как вызывает затруднения при сравнении корреляционных моментов различных пар случайных величин. Для устранения этого недостатка вводят новую числовую характеристику – коэффициент корреляции или нормированный корреляционный момент.

Коэффициентом корреляции случайных величин X и Y называют отношение корреляционного момента к произведению средне – квадратичных отклонений этих величин:

.

Для независимых величин ; для величин, связанных между собой линейной зависимостью, или . Равенство нулю коэффициента корреляции еще не свидетельствует о том, что случайные величины являются независимыми.

38 Теорема сложения математических ожиданий.

Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин.

Постановка задачи. Дана система случайных величин (X,Y), плотность распределения которой известна. Требуется определить математическое ожидание суммы случайных величин M(Z)=M(X+Y).

Используя определение математического ожидания случайной непрерывной величины, получаем

Т.е. .

Если случайная величина , то . (4.1)

Эта теорема справедлива как для зависимых, так и для независимых величин.

Математическое ожидание линейной функции случайных величин равно той же линейной функции от математических ожиданий этих величин:

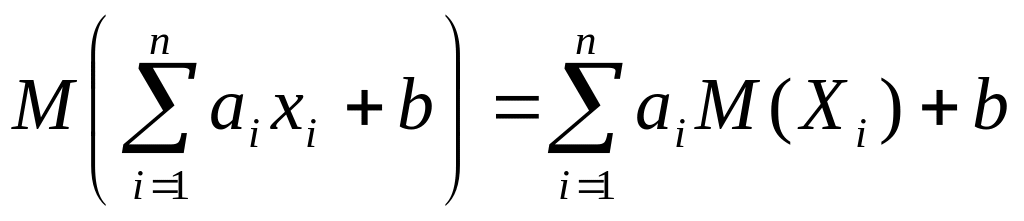, где - неслучайные величины.

В случае комплексного характера случайной величины математическое ожидание ее также будет комплексным:

.

Математическое ожидание произведения нескольких независимых случайных величин равно произведению математических ожиданий этих случайных величин.

Постановка задачи.

Пусть случайная величина имеет закон распределения . Требуется определить МО M(Z) случайной величины Z.

.

Поскольку случайные величины являются независимыми, то функцию можно представить как произведение сомножителей:

.

Тогда математическое ожидание случайной величины Z будет равно

. Откуда

. (4.2)

Выражение (4.2) не применимо для зависимых случайных величин.

Математическое ожидание произведения двух зависимых случайных величин равно сумме произведений их математических ожиданий и корреляционного момента:

. (4.3)

Справедливость этого свойства вытекает из формулы корреляционного момента.

Математическое ожидание нелинейной функции случайных аргументов. Пусть случайная величина Z является функцией случайных аргументов . Требуется определить МО M(Z).

Поставленная задача решается точно только для некоторых частных случаев. В общем случае при решении этой задачи сначала нелинейную функцию в окрестности точки линеаризуют разложением ее в ряд Тейлора:

. Применяя к этой случайной величине свойство МО линейной функции, находим:

, (4.4)

учитывая, что .

Таким образом, МО нелинейной функции случайных аргументов равно этой же функции от математических ожиданий этих аргументов.