3 Геометрический способ определения вероятностей событий.
Данный способ применяют тогда, когда опыт относится к схеме случаев, но число благоприятных случаев и число равновозможных и несовместных случаев подсчитать невозможно, но можно поставить этим числам в однозначное соответствие определенные длины, площади, объемы и другие физические величины.
Пример 4: Имеется некоторый монтажный провод длиной L. Разрыв может произойти в любой точке с одинаковой вероятностью. Определить вероятность того, что разрыв произойдет на участке длиной l, если считать, что разрыв одновременно в нескольких точках невозможен.
Решение.
Поставив в соответствие числам m и n длины l и L, вероятность разрыва провода на участке l можно определить по формуле
Рассмотренный пример иллюстрирует геометрическое определение вероятности: вероятность случайного события есть отношение длины участка благоприятного появлению события к длине всего провода. Геометрическое определение вероятности является обобщением классического определения на случай, когда число равновозможных исходов бесконечно.
4 Теорема сложения вероятностей для совместимых событий.
Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их совместного появления. Т.е., если события A и B совместны, то
Доказательство.
Пусть испытание имеет n элементарных равновозможных исходов, из которых событию A благоприятны m исходов, событию B благоприятны k исходов, событию AB благоприятны l исходов, тогда
Число исходов,
благоприятных сумме A+B
событий A
и B
будет равно`
поэтому
что и требовалось доказать.
В случае трех совместных событий вероятность их суммы вычисляется по формуле
В случае же n совместных событий вероятность их суммы может вычисляться по формуле
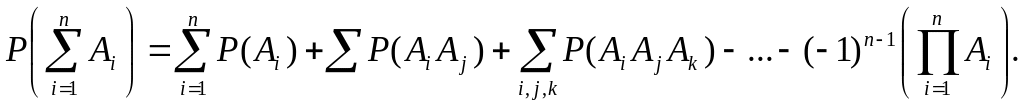
Пример 3: Три стрелка стреляют по одной цели. Найти вероятность поражения цели при одном залпе, если вероятности поражения цели соответственно равны: 0,8; 0,8; и 0,9.
Решение.
Рассмотрим события:
A – поражение цели;
B – поражение цели I - м стрелком (I =1,2,3).
Так как требуется
определить вероятность поражения цели
вообще, то событие A
есть сумма
событий
являющихся совместными и независимыми.
Поэтому
5 Теорема сложения вероятностей для несовместимых событий.
Вероятность суммы
нескольких несовместных событий равна
сумме вероятностей этих событий,
т.е.
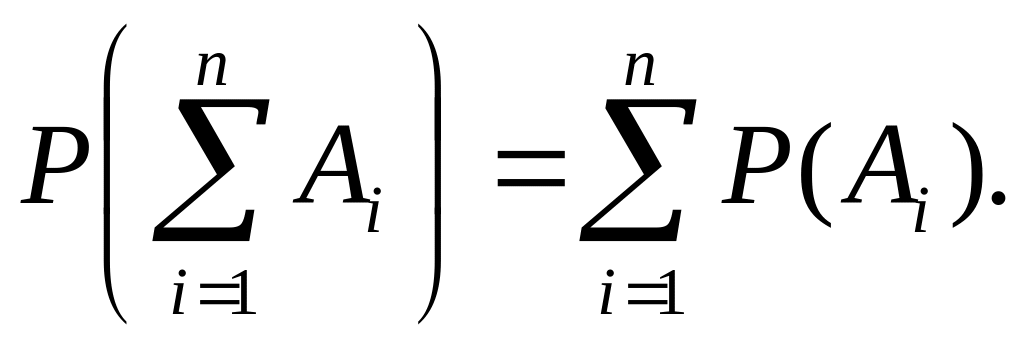
Эта теорема является частным случаем теоремы сложения вероятностей для несовместных событий.
Следствия из теоремы.
Следствие 1. Если
события
несовместны
и образуют полную группу, то
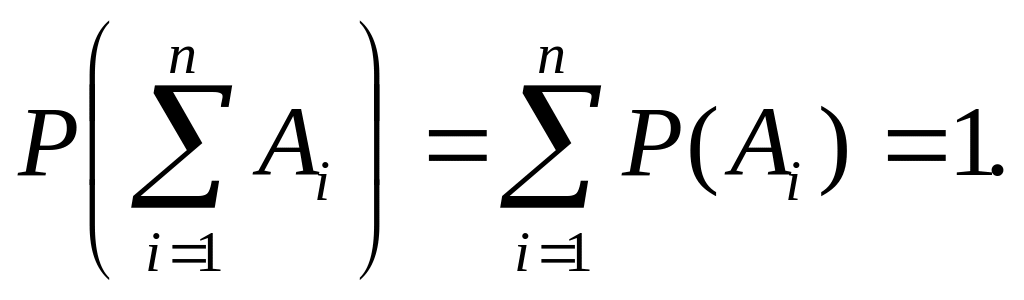
Следствие 2. Два несовместных события, образующих полную группу, называют противоположными событиями. Сумма вероятностей противоположных событий равна единице, т.е.
.
6 Зависимые и независимые события. Условные вероятности событий.
Для нахождения вероятностей совместного появления событий необходимо уточнить понятия зависимости и независимости событий.
Событие A называют зависимым от события B, если вероятность события A зависит от того, произошло событие B или нет.
Событие A будем называть независимым от события B, если вероятность события A не зависит от того, произошло или не произошло событие B.
Пример зависимых событий. В ящике 3 белых и 5 черных шаров. Последовательно берутся 2 шара. Определить вероятность того, что второй шар будет белым.
Решение.
Случай 1. Если первым
вынут черный шар, то вероятность того,
что второй шар будет белым равна
Случай 2. Если первый
шар оказался белым, то вероятность того,
что второй шар будет белым равна
Примером независимых событий является этот же пример, но с возвращением первого шара в ящик.
Вероятность появления зависимого события называют условной вероятностью, а вероятность появления независимого события - безусловной вероятностью. Под условной вероятностью P(A/B) события A понимают вероятность этого события, которая вычислена при условии, что событие B произошло.
Если события A и B независимы, то условная вероятность события A равна безусловной вероятности этого события, т.е.
Если же события A и B зависимы, то условная вероятность события A неравна безусловной вероятности этого события, т.е.
