14 Вероятность попадания случайной величины на заданный участок.

Пусть случайная непрерывная величина X может принять частное значение в интервале , причем известна ее функция распределения F(x). Требуется найти вероятность попадания ее в этот интервал, т.е. .

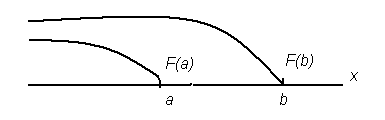
Рисунок 4 Определение значений функции распределения на границах интервала

По определению значение функции распределения F(b) в точке b является вероятностью того, что случайная величина примет значение меньшее b, а значение функции распределения F(a) в точке a - вероятностью того, что случайная величина примет значение меньшее a. Следовательно, вероятность попадания случайной величины в этот интервал будет определяться разностью значений функций распределения в граничных точках, т.е.

. (2.1)

Рисунок 5 Определение по функции распределения

Вероятность попадания случайной величины на заданный участок равна приращению функции распределения на этом участке (рис. 5).

Пример 1: Прибор рассчитан на входное напряжение не большее 220 Вольт, а напряжение сети является случайной величиной с функцией распределения

если 210<X<230;

F(x) =0, если X<210;

F(x) =1, если X>230.

Определить вероятность отказа прибора из–за непостоянства напряжения сети.

Решение.

Обозначим через A – событие отказа прибора в работе; V – случайная величина напряжения в сети.

P(A)=P(220<V<230)=F(230)-F(220).

F(230)=(x-210)/20=(230-210)/20=1;

F(220)=(220-210)/20=0,5. Откуда P(A)=1-0,5=0,5.

15 Математическое ожидание случайной величины и ее свойства.

Математическим ожиданием (МО) случайной величины называют ее среднее значение, определяемое по следующим формулам.

Для случайных дискретных величин МО равно

, где - частное значение случайной дискретной величины; - вероятность ее появления.

Для случайной непрерывной величины МО определяется выражением

, где x – частное значение случайной непрерывной величины; f(x)dx – элемент вероятности.

Математическое ожидание случайной величины представляет собой центр, около которого группируются частные значения ее.

Свойства математического ожидания:

а) математическое ожидание случайной величины может быть положительным и отрицательным, целым и дробным, и обладает размерностью случайной величины;

б) не все случайные величины имеют МО. Случайные величины не имеют МО, если или ;

в) математическое ожидание постоянной величины равно самой постоянной величине, т.е. .

г) постоянную величину можно выносить за знак математического ожидания, т.е.

.

Частный случай математического ожидания. Пусть случайная величина X может принимать только два частных значения . Тогда вероятности появления этих частных значений будут равны

.

Откуда математическое ожидание .

Следовательно, математическое ожидание такой случайной величины равна вероятности того, что случайная величина примет значение равное единице.

Пример 1: В технической системе имеется n элементов. Вероятность выхода из строя элемента в течении N часов работы равна p. Требуется определить математическое ожидание числа отказавших элементов в течении N часов работы.

Решение.

Обозначим через X – случайную величину числа отказавших элементов, а через M[X] - математическое ожидание этого числа.

Для использования формулы математического ожидания определяем из условия задачи, что случайная величина X принимает частные значения , причем .

Тогда математическое ожидание числа отказавших элементов будет равно

.

Отсюда следует, что если случайная величина X подчиняется биномиальному закону, то ее МО равно произведению числа опытов на вероятность появления события в одном опыте.