
- •Ответы на вопросы.
- •1 Способ непосредственного подсчета вероятностей событий.
- •2 Статистический способ определения вероятностей событий.
- •3 Геометрический способ определения вероятностей событий.
- •4 Теорема сложения вероятностей для совместимых событий.
- •5 Теорема сложения вероятностей для несовместимых событий.
- •6 Зависимые и независимые события. Условные вероятности событий.
- •7 Теорема умножения вероятностей.
- •8 Формула полной вероятности.
- •9 Теорема гипотез (Формулы Бейеса).
- •10 Повторение испытаний. Формулы Бернулли.
- •11 Понятие случайной величины. Виды законов распределения.
- •12 Функция распределения случайной величины и ее свойства.
- •13 Плотность распределения случайной величины и ее свойства.
- •14 Вероятность попадания случайной величины на заданный участок.
- •15 Математическое ожидание случайной величины и ее свойства.
- •16 Дисперсия случайной величины и ее свойства. Среднее квадратичное отклонение.
- •17 Закон равномерной плотности.
- •18 Нормальный закон распределения.
- •19 Экспоненциальный закон распределения.
- •20 Вероятность попадания случайной величины на заданный участок.
- •21 Теорема Чебышева.
- •22 Теорема Бернулли.
- •23 Элементы математической статистики. Генеральная и выборочная совокупности. Статистическое распределение выборки.
- •24 Эмпирическая функция распределения, ее построение по опытным данным.
- •25 Гистограмма частот и относительных частот.
- •26 Статистические оценки параметров распределения. Несмещенные, эффективные и состоятельные оценки.
- •27 Интервальные оценки параметров распределения. Доверительный интервал.
- •28 Интервальная оценка математического ожидания нормального распределения при известном среднем квадратичном отклонении.
- •29 Интервальная оценка среднеквадратического отклонения нормального распределения.
- •30 Функция распределения системы случайных величин и ее свойства.
- •31 Плотность распределения системы случайных величин и ее свойства.
- •32 Законы распределения отдельных случайных величин, входящих в систему.
- •33 Условные законы распределения случайных величин.
- •34 Числовые характеристики системы двух дискретных случайных величин.
- •35 Числовые характеристики системы двух непрерывных случайных величин.
- •36 Условное математическое ожидание. Уравнение линии регрессии.
- •37 Корреляционный момент. Коэффициент корреляции.
- •38 Теорема сложения математических ожиданий.
- •39 Теорема сложения дисперсий.
- •40 Математическое ожидание линейной функции случайных аргументов.
- •44 Закон распределения суммы двух случайных величин.
- •45 Композиция одномерных нормальных законов.
- •46 Понятие о центральной предельной теореме.
- •47 Понятие о случайной функции.
- •48 Закон распределения случайной функции.
- •49 Математическое ожидание и дисперсия случайной функции.
- •50 Корреляционная функция случайного процесса и ее свойства. Нормированная корреляционная функция.
- •51 Определение характеристик случайной функции по опытным данным.
- •52 Сложение случайных функций.
- •53 Сложение случайной функции со случайной величиной.
- •54 Умножение случайной функции на неслучайную функцию.
- •55 Стационарная случайная функция и свойства ее характеристик.
32 Законы распределения отдельных случайных величин, входящих в систему.
Пусть имеется система
случайных величин (X,
Y),
причем известна ее функция распределения
F(X,
Y)
или плотность
распределения f(x,
y).
Требуется найти законы распределения
случайных величин X,
Y,
входящих в систему, т.е. определить
выражения для функций
![]() .
.
Согласно второму
свойству функции распределения случайных
величин X,
Y
равны
![]() .
Поэтому для получения функции распределения
одной случайной величины, входящей в
систему необходимо в функцию распределения
системы вместо другой случайной величины
подставить «
.
Поэтому для получения функции распределения
одной случайной величины, входящей в
систему необходимо в функцию распределения
системы вместо другой случайной величины
подставить «![]() ».
Для отыскания выражения плотности
распределения, например, случайной
величины X
воспользуемся определением ее, т.е.
».
Для отыскания выражения плотности
распределения, например, случайной
величины X
воспользуемся определением ее, т.е.
![]() ,
или окончательно
,
или окончательно
![]() .
По аналогии
.
По аналогии
![]() .
.
Следовательно, для получения плотности распределения одной случайной величины, входящей в систему, необходимо плотность распределения системы f(x, y) проинтегрировать в бесконечных пределах по другой случайной величине как переменной.
Пример 1. Дана
система случайных величин (X,
Y)
с плотностью распределения
![]() для всех точек внутри треугольника
(рис. 3.7а), вне треугольника f(x,
y)=0.
Требуется определить
для всех точек внутри треугольника
(рис. 3.7а), вне треугольника f(x,
y)=0.
Требуется определить
![]() .
.
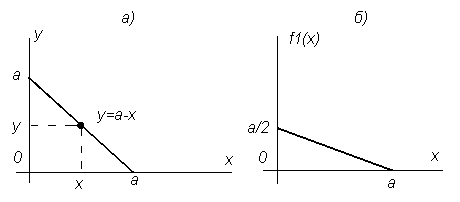
Рисунок 3.7 Иллюстрация к примеру
Решение.
Используя полученное
выражение для плотности распределения
случайной величины X,
получим
![]() .
Аналогично находим выражение для
плотности распределения случайной
величины Y
.
Аналогично находим выражение для
плотности распределения случайной
величины Y
![]() (см. рис. 3.7б).
(см. рис. 3.7б).
33 Условные законы распределения случайных величин.
Ранее были получены формулы для нахождения плотностей распределения составляющих величин по плотности распределения системы двух случайных величин f(x, y).
В ряде случаев бывает необходимо определять плотность распределения системы двух случайных величин f(x, y) по известным плотностям распределения отдельных случайных величин , входящих в систему.
Для решения этой задачи кроме плотностей распределения отдельных случайных величин необходимо знать их взаимные связи и зависимость между ними. Эта зависимость характеризуется условными законами распределения, которые являются аналогами условных вероятностей.
Условным законом распределения случайной величины X, входящей в систему (X, Y) называют ее закон распределения, вычисленный при условии, что другая случайная величина Y приняла определенное значение y.
Условные функции распределения случайных величин X и Y будем обозначать через F(x/y) и F(y/x) соответственно, а условные плотности распределения – через f(x/y) и F(y/x).
Постановка задачи. Пусть имеется система случайных величин (X, Y), причем известна ее плотность распределения f(x, y). Требуется найти условную плотность распределения f(x/y) случайной величины X при условии, что случайная величина Y приняла определенное значение y.
Для решения задачи рассмотрим элементарный прямоугольник со сторонами d x, d y (рис. 3.8).

Рисунок 3.8 Элементарный прямоугольник со сторонами d x, d y
Обозначим через C – событие попадания случайной точки в прямоугольник C, через A - событие попадания случайной точки в полосу A, а через B - событие попадания случайной точки в полосу B.
Так как событие C является произведением событий A и B, поскольку может произойти только при появлении и события A и события B, то вероятность события C можно определить с помощью теоремы произведения зависимых событий, т.е.
![]() .
.
Откуда
![]() ,
но
,
но
![]() и
и
![]() .
.
Тогда
![]() .
Разделив обе части этого равенства на
.
Разделив обе части этого равенства на
![]() ,
получим
,
получим
![]() .
В этом выражении отношение
.
В этом выражении отношение
![]() ,
так как оно представляет собой количество
условной вероятности, приходящейся на
единицу длины случайной величины X,
т.е. является условной плотностью
распределения случайной величины X,
при условии, что случайная величина Y
приняла
определенное значение
y.
,
так как оно представляет собой количество
условной вероятности, приходящейся на
единицу длины случайной величины X,
т.е. является условной плотностью
распределения случайной величины X,
при условии, что случайная величина Y
приняла
определенное значение
y.
Следовательно,
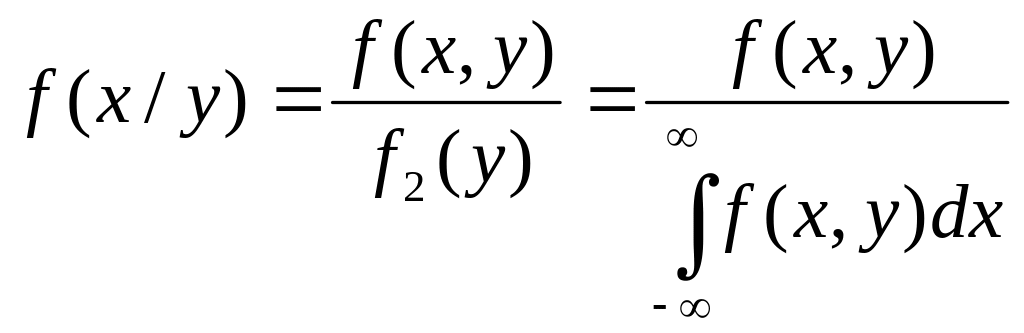 ,
а
,
а
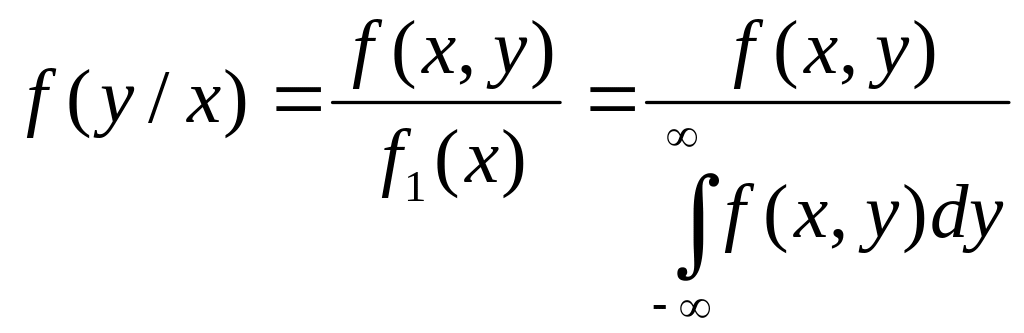 .
.
Пример 3. В условиях примера 1 определить условную плотность распределения f(x/y) случайной величины X.
Решение. Так как
,
![]() ,
,
![]() ,
то
,
то
![]() ,
т.е.
,
т.е.
![]() .
.
Если случайные величины дискретные, то вместо условных плотностей распределения определяются условные вероятности
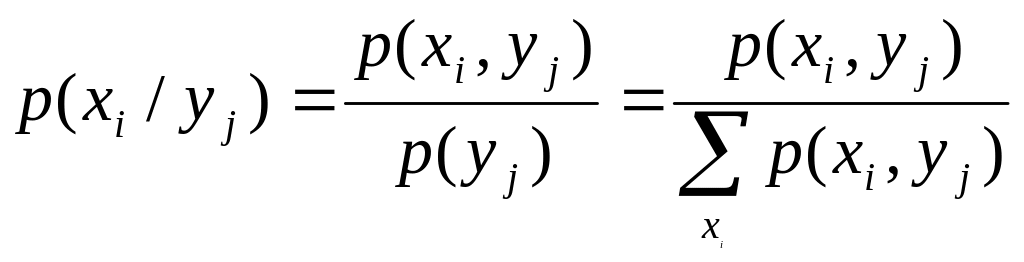 ,
а
,
а
 .
.
