
- •Федеральное агентство по образованию
- •Содержание
- •В машиностроении
- •3.1. Система нормирования и обозначения шероховатости
- •3.2. Нормирование, методы и средства контроля отклонения
- •3.3. Контроль гладких цилиндрических деталей калибрами ……... 60
- •1. Основные понятия о взаимозаменяемости в машиностроении
- •1.1. Понятие о взаимозаменяемости и ее виды
- •1.2. Понятия о размерах, отклонениях, допусках и посадках
- •1.3. Обозначение посадок и предельных отклонений
- •2. Единая система допусков и посадок
- •2.2. Система допусков и посадок гладких цилиндрических сопряжений
- •3. Система нормирования и методы контроля качества поверхностей деталей
- •3.1. Система нормирования и обозначения шероховатости поверхности
- •3.1.1. Параметры шероховатости
- •3.1.2. Обозначение шероховатости поверхности на чертежах
- •3.2. Нормирование, методы и средства контроля отклонения формы и взаимного расположения поверхностей деталей
- •3.2.1. Классификация отклонений геометрических
- •3.2.2. Система нормирования отклонений формы и расположения
- •3.2.3. Отклонение формы цилиндрических поверхностей
- •3.2.4. Отклонение формы плоских поверхностей
- •3.2.5. Отклонение расположения поверхностей
- •3.2.6. Обозначение на чертежах допусков формы
- •3.3. Контроль гладких цилиндрических деталей калибрами
- •3.3.1. Назначение и классификация калибров
- •3.3.2. Допуски калибров
- •3.3.3. Расчет исполнительных размеров калибров
- •3.3.4. Маркировка калибров
- •0,039 0
- •4. Расчет размерных цепей
- •4.1. Термины и определения, относящиеся
- •4.2. Методы расчета размерных цепей и задачи,
- •4.3. Расчет размерных цепей методом
- •4.3.1. Расчет размерных цепей способом “максимума – минимума”
- •4.3.2. Расчет размерных цепей способом равных допусков
- •4.4.1. Способ групповой взаимозаменяемости (селективная сборка)
- •Vk– величина компенсирующего звена.
- •5.2.2. Основные параметры крепежных,
- •5.3.4.1. Допуски и посадки при центрировании по боковым поверх-
- •5.5.1. Назначение и виды зубчатых передач
- •5.5.2. Система допусков цилиндрических зубчатых колес
- •5.5.2.2. Плавность работы передач
- •6.2. Документы по стандартизации и виды стандартов
- •6.3 Организация работ по стандартизации в Российской Федерации
- •7.1. Сущность и содержание сертификации
- •7.3.3. Порядок проведения сертификации продукции
- •7.4. Российские системы сертификации
- •7.6. Перспективные задачи развития сертификации
Vk– величина компенсирующего звена.
В данном случае должно обеспечиваться условие
n
VK≥ ∑TAi –TA0 , (4.37)
i=1
При наличии в размерной цепи размеров, которые в процессе эксплуатации могут изменяться по величине (износ, температурные и силовые деформации и т. д.), к величине компенсации К следует добавлять величину ожидаемого изменения составляющих размеров.
Метод регулирования позволяет достичь высокой точности механизма и поддерживать ее в процессе эксплуатации при расширенных допусках всех размеров размерной цепи. Особую ценность этот способ представляет для решения размерных цепей, в которых имеются изменяющиеся в процессе эксплуатации размеры. К недостаткам данного способа следует отнести увеличение числа звеньев размерной цепи, что усложняет конструкцию, сборку и эксплуатацию.
4.5. Теоретико – вероятностный метод расчета
размерных цепей
При выводе формул (4.2) – (4.4) для расчета размерных цепей способом “максимума – минимума” предполагалось, что в процессе обработки деталей или сборки все звенья размерной цепи могут принимать либо максимальные значения, либо минимальные. Однако на практике это маловероятно, так как отклонения размеров в основном группируются около середины поля допуска и сочетание деталей с такими отклонениями происходит наиболее часто. Если допустить очень малую вероятность (например, 0,27 %) несоблюдения предельных значений замыкающего звена, то можно существенно расширить допуски составляющих звеньев, что позволит снизить себестоимость изготовления деталей. На этих положениях и основан теоретико–вероятностный метод расчета размерных цепей.
Первая задача. Предполагая, что погрешности составляющих и замыкающего звена размерной цепи подчиняются закону нормального распределения (закону Гаусса), а границы рассеяния (6σ) совпадают с границами полей допусков можно принять ТАi= 6σАi или σАi= 1/6TAi. Соответственно будут выполняться равенства ТА0= 6σА0 или σА0= 1/6TA0. При этом у 0,27 % деталей размеры замыкающих звеньев могут выходить за пределы поля допуска.
Используя уравнение суммирования погрешностей можно записать
n

 σ∑
= ∑σx2i
, (4.38)
σ∑
= ∑σx2i
, (4.38)
i=1
где σ∑ − суммарная погрешность размеров деталей, входящих в размерную цепь;
σxi − текущее значение погрешности i – го звена размерной цепи;
n – число составляющих звеньев размерной цепи.
После подстановки значений σАi и σА0в уравнение (4.38) и проведения соответствующие преобразования получим уравнение для определения допуска замыкающего звена
n

 ТА0
= ∑TA2i
, (4.39)
ТА0
= ∑TA2i
, (4.39)
i=1
После определения ТА0по формуле (4.17) находят координату середины поля допуска замыкающего звенаEc(А0), а по уравнениям (4.11), (4.12) – величиныEs(A0) иEi(A0).
Формула (4.39) выведена исходя из предположения, что распределение действительных размеров подчиняется закону нормального распределения, центр группирования размеров совпадает с серединой поля допуска, а величина рассеяния размеров не превышает допуска.
На практике могут быть случаи, когда закон распределения размеров несимметричен, а центр группирования размеров не совпадает с серединой поля допуска (рисунок 4.5)
m










− 3σAi + 3σAi




























T

 Ai
Ai





TAi / 2 TAi / 2


Ec (Ai) αi ·(TAi / 2)



Eм (Ai)

Рисунок 4.5. Координата центра группирования для несимметричной кривой
Координата центра группирования для несимметричного закона распределения может быть определена по формуле
Eм (Ai) = Ec (Ai) + αi · (TAi / 2), (4.40)
где αi – коэффициент относительной асимметрии несимметричной кривой распределения отклонений i – го размера.
Коэффициент αi определяет величину смещения центра группирования отклонений относительно середины поля допуска TAi и выражается в долях половины допуска. Из формулы (4.40) можно определить величину коэффициента αi.
αi = [Eм (Ai) – Ec (Ai)] / (0,5·TAi). (4.41)
Если поле допуска симметрично относительно номинального размера, а закон распределения является нормальным, Ec(Ai) = 0,Eм(Ai) = 0 иαi = 0. При условии асимметрии кривой распределения размеров с коэффициентом асимметрииαi, координата середины поля допуска равна
Ec (Ai) = Eм (Ai) – αi · (TAi/2). (4.42)
Координаты середины поля допуска и предельные отклонения замыкаю-щего звена определяют по уравнениям (4.17), (4.11) и (4.12) соответственно после расчета Ec(Ai) для асимметричной кривой распределения по уравнении. (4.42). Следовательно, порядок расчета координаты середины поля допуска и предельных отклонений замыкающего звена для симметричного и асимметричного распределения размеров отличается только в одном – для асимметричного распределения расчеты ведутся с учетом коэффициента относительной асимметрии кривой распределения размеровαi.
В производственных условиях случайные погрешности размеров деталей могут распределяться не по закону нормального распределения (кривой Гаусса). В этом случае при определении допуска замыкающего звена для любого закона распределения в расчетную формулу вводиться коэффициент относительного рассеяния размеров
n

 ТА0
= 1/k0
·
∑ TA2i
k2i
,
(4.43)
ТА0
= 1/k0
·
∑ TA2i
k2i
,
(4.43)
i=1
где k0, ki – коэффициенты, характеризующие отличие закона распределения погрешностей i – го и замыкающего звеньев от нормального распределения по закону Гаусса.
Коэффициент ki определяется из соотношения ki = 6σ/Vm (где Vm – предельное поле рассеяния случайной величины).
Для закона нормального распределения Vm= 6σ. В этом случае
ki= 6σi / 6σi= 1. (4.44)
Для закона равной вероятности
k
 i= 6σi/ (2 √ 3σi)
= 1,73. (4.45)
i= 6σi/ (2 √ 3σi)
= 1,73. (4.45)
При распределении по закону распределения близкому к закону Симпсона (закону треугольника) значение kiравно
k i= 6σi/ (2 √ 6σi
) = 1,22. (4.46)
i= 6σi/ (2 √ 6σi
) = 1,22. (4.46)
Эффективность применения теоретико – вероятностного метода расчета размерных цепей очевидна из следующего примера.
Предположим, что размерная цепь состоит из четырех составляющих звеньев с равными допусками ТА1= ТА2= ТА3= ТА4. Тогда по формуле (4.39) допуск замыкающего звена равен

ТА0= √ 4 ТА2i = 2ТАiоткудаTАi– 1/2TA0.
При решении задачи по способу “максимума – минимума” будем иметь
n
ТА0= ∑TAi= ТА1 +ТА2+ТА3+ТА4= 4ТАi , откуда ТАi= 1/4TA0
i=1
Как видно из примера, применение теории вероятностей в условиях приведенного примера при одинаковом допуске замыкающего звена (в сопоставлении со способом “максимума – минимума”) расширить в два раза допуски составляющих звеньев. Но при этом у 0,27 % деталей размерной цепи (три детали из тысячи) предельные значения замыкающего звена могут быть не выдержаны, то есть имеется возможность появления брака.
Вторая задача. Допуски составляющих размеров при известном допуске замыкающего звена можно рассчитывать четырьмя способами.
1. При способе равных допусков принимают, что величиныTAi,Ec(Ai),αi иki для всех составляющих звеньев размерной цепи одинаковы. По заданной величине ТА0определяют средние допускиTmAiудовлетворяющие равенству (4.39) или (4.43).
Из равенства (4.43) получаем

ТА0= √(m– 1)TmA2ik2i, откуда средний допуск равен

TmAi=TA0/ (ki· √m– 1). (4.47)
Если коэффициент kiнеодинаковый для всех звеньев размерной цепи, то формула (4.47) имеет вид
m

 -1
-1
TmAi = TA0 / ( ∑ ki2 ). (4.48)
i=1
Найденные значения TmAiиEc(Ai) корректируют, учитывая требования конструкции и возможность применения методов обработки деталей, при которых экономическая точность близка к требуемой точности размеров.
2. При способе равной точности(назначение допусков одного квалитета) расчет аналогичен расчету размерных цепей методом полной взаимозаменяемости по уравнению (4.26), но с учетом коэффициентаki, характеризующего отклонение закона распределения размеров размерной цепи от закона нормального распределения Гаусса. Решая совместно уравнения (4.26) и (4.43) относительно числа единиц допуска (а) получим
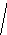


 n
3
n
3
am = TA0 · k0 / ∑(0,45√ D + 0,001D)2k2i. (4.49)
i=1
3. Способ пробных расчетовзаключается в назначении экономически целесообразных для данного производства допусков на составляющие звенья размерной цепи. При этом учитываются конструктивные требования, опыт эксплуатации подобных машин и механизмов и проверенных для данного производства значений коэффициентовαi иki. С целью повышения надежности, долговечности и точности, а также обеспечения функциональной взаимозаменяемости машин допуски и предельные отклонения составляющих звеньев и замыкающего звена ответственных узлов выпускаемых машин корректируют в сторону их ужесточения. Этим самым создают запас на износ. После назначения допусков и отклонений правильность расчетов проверяют по уравнению (4.43). Если условие по уравнению (4.43) не выполняется, то допуски, а иногда и номинальные размеры составляющих звеньев корректируют.
4. Способ равного влиянияоснован на том, что допустимое отклонение каждого составляющего звена размерной цепи должно вызывать одинаковое изменение размера замыкающего звена. Этот способ применяют при решении плоских и пространственных размерных задач.
4.6. Расчет плоских и пространственных размерных цепей
Плоские и пространственные размерные цепи рассчитывают теми же методами, что и линейные. Для этого плоские или пространственные цепи приводят к виду линейных. Осуществляется это путем проектирования размеров плоской цепи на одно направление, как правило, на направление совпадающее с направлением замыкающего (исходного) звена. Размеры пространственных цепей проектируются на две или три взаимно перпендикулярные оси.
В качестве примера рассмотрим плоскую пространственную размерную цепь с замыкающим звеном А0, определяющим максимальное продольное перемещение толкателя (рисунок 4.6). Приведем размерную цепь к линейной у которой размер А′5= А5 ·cosα(на рисунке 4.6, в А3есть А′3).
Используя уравнения (4.5), (4.39) и (4.43) определяем допуск замыкающего звена:
по способу “максимума – минимума”
n
ТА0 = ∑ (∂A0 /∂Ai) · TAi ; (4.50) i=1







 А2
А1
А2
А1






























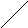












А






 5
5











































































α












А4 А3 А0




 а
а


 А2
А1
А2
А1



А5
α
А



 3
А0
3
А0




А 4
4
б



 А5
А2
А1
А5
А2
А1




 А4
А3
А0
А4
А3
А0



в
Рисунок 4.6. Эскиз узла (а) плоская (б) и линейная (в) размерные цепи
теоретико – вероятностным методом
n
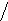

ТА0 = ∑(∂A0 /∂Ai)2 · TAi k2i ; (4.51)
i=1
где ∂A0 /∂Ai – частная производная функция замыкающего размера по i – му составляющему звену (эту величину называют также передаточным отношением ui).
Передаточные отношения характеризуют степень и характер влияния погрешностей размеров составляющих звеньев на размер замыкающего звена. Для параллельных звеньев размерной цепи все передаточные отношения у4величивающих звеньев равны “плюс” единице, а уменьшающих – “минус” единице. При расчета допуска замыкающего звена передаточные отношения ∂A0 /∂Ai необходимо принимать по абсолютным значениям.
Рассмотрим пример расчета допуска замыкающего звена хплоской размерной цепи (рисунок 4.7). Номинальные размеры и отклонения составляющих звеньев размерной цепи, а также углы наклона β и γ заданы. При этом, углы наклона размеров допусками не ограничены.


 А1
А2
А1
А2
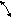
β γ
Х
Рисунок 4.7. Плоская 3 – х звенная размерная цепь
Номинальная величина размера х равна
х=f(A1,A2) =A1 ·cosβ+A2·cosγ.
Допуск замыкающего размера Тхопределяется по формуле (4.50)
Тх = (∂f / ∂A1) · TA1 + (∂f / ∂A2) · TA2 , (4.52)
Где ТА1 и ТА2 – допуски составляющих звеньев.
Передаточные отношения ∂f/ ∂A1=cosβ; ∂f/ ∂A2 =cosγ.
Тригонометрические функции углов принимаются условно постоянными, так как погрешности сторон треугольника незначительны. Подставляя найденные значения передаточных отношений в формулу (4.52) получим допуск замыкающего звена
Tx = TA1 cosβ + TA2 cosγ. (4.53)
Если размерная цепь рассчитывается теоретико – вероятностным методом, то уравнение (4.53) имеет вид

Тх = √ k21 · TA21·cosβ + k22 ·TA22 ·cosγ , (4.54)
где k1 и k2 – коэффициенты относительного рассеяния отклонений состав- ляющих звеньев.
Рассмотренные методы решения размерных цепей могут применяться для решения любых размерных задач. Выбор того или иного метода определяется конкретной размерной задачей и, в первую очередь, необходимой точностью ее решения.
5. ДОПУСКИ И ПОСАДКИ ТИПОВЫХ СОПРЯЖЕНИЙ
МЕХАНИЗМОВ И МАШИН
5.1 Система допусков и посадок подшипников
качения
5.1.1. Назначение и классы точности подшипников качения
Подшипники качения являются широко распространенными стандартными узлами, изготавливаемыми на специализированных подшипниковых заводах. Они применяются практически во всех машинах и механизмах в качестве опор валов и осей. Подшипники качения обладают полной внешней взаимозаменяемостью (по присоединительным размерам), то есть по наружному Dи внутреннемуdдиаметрам колец. В свою очередь подшипники качения обладают неполной внутренней взаимозаменяемостью. Обусловлено это малыми допусками и зазоров и допусками на размеры тел качения (шариков или роликов). В связи с этим детали подшипников качения изготавливают с расширенными допусками, а затем применяют селективную сборку. Полная взаимозаменяемость по присоединительным размерам позволяет производить быструю замену, вышедших из строя подшипников с сохранением требуемого качества узлов.
При прочих равных условиях качество подшипников качения определяется следующими факторами:
точностью присоединительных размеров d,Dи шириной кольца В, а для роликовых радиально – упорных подшипников – точностью монтажной высоты Т (рисунок 5.1);
T


B
B


 r
r





































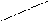


























D


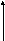




D


 d
d
d






а б
Рисунок 5.1. Схемы подшипников качения: радиального (а) и конического радиально – упорного (б)
точностью формы и взаимного расположения поверхностей колец подшипников и их шероховатостью;
точностью формы, размеров тел качения в одном подшипнике и шероховатостью их поверхностей;
точностью вращения, которая характеризуется осевым и радиальным биением беговых дорожек колец подшипника, а также торцовым биением колец подшипника.
В зависимости от указанных факторов, определяющих точность подшипников по стандарту СТ СЭВ 774 – 77установлено пять классов точности подшипников качения, обозначаемых цифрами (в порядке увеличения точности): 0; 6; 5; 4; 2. Различия в требованиях к точности для каждого класса очень существенны. Например, для радиальных и радиально – упорных подшипников качения d= 80 ….. 120 мм допустимое радиальное биение дорожки качения внутреннего кольца и биение торца подшипника 2 – го класса составляет 2,5 мкм, а у подшипников 0 – го класса указанные биения составляют 25 мкм, то есть различаются в 10 раз.
До появления стандарта СТ СЭВ 774 – 77 классы точности подшипников качения обозначались буквами, а не цифрами. Класс точности обозначался первой буквой его названия: Н – нормальный; П – повышенный; В – высокий; С – сверхвысокий; А – прецизионный. Новое и старое обозначение классов точности подшипников качения взаимосвязаны следующим образом:
0


 ;
6; 5; 4; 2
;
6; 5; 4; 2
Н; П; В; С; А.
По стандарту СТ СЭВ 774 – 77 класс точности подшипника качения указывается в обозначении подшипника, через тире перед условным его обозначением. Например, 6 – 205, 0 – 310 и т. д.
Выбирают класс точности подшипника исходя из предъявляемых требований к точности вращения, в соответствии с условиями работы механизма. Для большинства машин и механизмов общего назначения применяют подшипники качения класса 0 (нормального). Боле высокие классы точности подшипников применяют для больших частот вращения и в случаях необходимости обеспечения высокой точности вращения (шпиндели шлифовальных и прецизионных станков, подшипниковые узлы авиационных двигателей, высокоточные приборы и т. д.). Так, например, для гироскопических и других прецизионных (особо точных) приборов применяются подшипники качения класса 2.
5.1.2. Допуски и посадки подшипников качения
С целью сокращения номенклатуры выпускаемых подшипников качения их изготавливают с отклонениями наружного и внутреннего диаметров колец, не зависящими от посадок, по которым они будут монтироваться в машине или механизме. Для всех, без исключения, классов подшипников наружный диаметр наружного кольца (посадочный размер в корпус) изготавливается как основной вал. Следовательно, верхнее отклонение у него равно нулю, а нижнее имеет знак “минус” (рисунок 5.2, а).
Td
TD
T′d



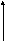 0
0 0
0
0
0 0
0

 d
d
 D
−
−
D
−
−
 а
б
а
б
Рисунок 5.2. Схемы полей допусков наружного (а) и внутреннего (б) колец подшипника качения
Внутреннее кольцо подшипника качения изготавливается с полем допуска основного отверстия (штриховой прямоугольник на рисунке 5.2, б), но для получения большего числа посадок кольца с небольшим натягом из числа переходных посадок, поле допуска внутреннего кольца переворачивается (сплошной прямоугольник на рисунке 5.2, б). Следовательно, для внутреннего кольца подшипника посадки с небольшим гарантированным натягом можно получить, используя основные отклонения, применяемые для переходных посадок: k,m,n. Посадки с большими натягами для подшипников качения не применяются, так как тонкостенные кольца подшипника будут деформироваться и возникнут сложности в обеспечении необходимого рабочего зазора между телами качения и беговыми дорожками колец.
В целях обеспечения высокого качества подшипниковых узлов непостоянство диаметров колец (овальность) и средняя конусообразность колец шариковых и роликовых радиально – упорных подшипников 5 – 2-го классов точности допускается не более 50% допуска на диаметры колец (Dmиdm). В свободном состоянии подшипника овальность и конусообразность могут быть больше 50% от допуска, но при монтаже подшипника его кольца выправляются. Вследствие овальности, конусообразности и других погрешностей при измерениях диаметры колец в разных сечениях могут быть неодинаковыми, что, безусловно, оказывает влияние на характер соединения кольца с соответствующей сопрягаемой деталью(посадка в корпус или на вал).
В связи с изложенным, стандартом устанавливаются предельные отклонения предельные отклонения номинальных значений D,dи среднего значения диаметровDm,dm . ВеличиныDmиdmопределяют как среднее арифметическое наибольшего и наименьшего значений диаметра, измеренных в двух крайних сечениях кольца. Для посадок колец подшипников качения применяют поля допусков, показанные на рисунке 5.3.
К


 лассы
точности подшипников
лассы
точности подшипников
0 6 5 4
2
6 5 4
2
Н
 8G5
8G5
G
 7
7
О тверстия
корпусов
тверстия
корпусов
H
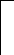 7H6H5
7H6H5
J
 s7
s7
J s6
s6
K 7
Js5
7
Js5
K
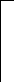
 5
5

 M7
K6
M7
K6
0













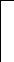



































 0
0
N







 7
7
M












 6
6
N





 6
6
− P7P7
P7P7



 DmНаружное
М5 кольцоM5
DmНаружное
М5 кольцоM5
N
 5
5
n5
В
 нутреннее
нутреннее
кольцо m5n4



 m6
n6
m6
n6



 k6
k5
m4
k6
k5
m4
k

 4
4

j s6
js5
s6
js5
j













 s4
s4


















































 h6
h5
0
h6
h5
0
0







 g6
g6






















f





 7
7
h 4
4
Валы
g 5
5
dmg4

Рисунок 5.3. Схема применяемых полей допусков для посадок колец подшипников качения
Из рисунка 5.3 видно, что для наружного и внутреннего колец подшипников качения поля допусков выполняются по различным квалитетам. Существует общая закономерность – размеры посадочных мест для внутреннего кольца подшипника (валы) выполняются на один квалитет точнее, чем размеры посадочных мест для наружного кольца. Эта закономерность распространяется на все классы точности подшипников.
Высокие требования предъявляются к шероховатости посадочных и торцовых поверхностей колец подшипников качения. Повышенные требования к шероховатости поверхностей предъявляются и для валов и посадочных мест корпусов. Например, у колец подшипников качения 4 и 2 – го классов точности диаметром до 250 мм шероховатость указанных выше поверхностей должна быть в пределах Rа = 0,63 … 0,32 мкм. Особые требования предъявляются к шероховатости поверхностей тел качения и беговых дорожек колец подшипников: например, уменьшение шероховатости этих поверхностей отRа = 0,32....0,16 мкм доRа = 0,16 … 0,06 мкм повышает ресурс подшипника более чем в два раза, а дальнейшее уменьшение шероховатости поверхностей тел качения и беговых дорожек колец подшипника доRа = 0,08 .. 0,04 мкм увеличивает ресурс подшипника еще на 40 %.
Примеры указания требований к точности деталей подшипникового узла приведены на рисунке 5.4. Для соединения колец подшипников с валами и корпусами применяют специальные, так называемые, подшипниковые посадки. Отличие подшипниковых посадок от посадок по ГОСТ 25346 – 89 состоит в том, зазоры и натяги в этих посадках имеют другие величины. Это обусловлено тем, что предельные отклонения колец подшипников качения по СТ СЭВ 774 – 77 отличаются от предельных отклонений устанавливаемых ГОСТ 25346 – 89 (СТ СЭВ 145 – 88). Если для соединения колец подшипника с валом и корпусом принять предельные отклонения размеров колец по ГОСТ 25346 – 89 (СТ СЭВ 145 – 88), то характер соединения будет совершенно другой.
По СТ СЭВ 774 – 77 посадка подшипника качения указывалась одним полем допуска. Например, 40k6,90Н7, то есть указывалось поле допуска сопрягаемой с кольцом подшипника детали, а поле допуска кольца подшипника не указывалось. По ГОСТ 3325 – 85 в подшипниковых посадках наружное и внутреннее кольцо обозначаются буквойlиL, после которых указывается класс точности подшипника. Например,l0,L0. Цифра 0 означает класс точности подшипника качения. Следовательно, посадки колец подшипника будут выглядеть следующим образом:40k6/L0,90Н7/l0.




















































































































 50H7
50H7



























































































 50Н7/t690H7/l0
б
50Н7/t690H7/l0
б
а
40Е9/k790H8/d10

 40L0/k6
40L0/k6
 90d10
90d10





















 90Н7
90Н7


















R








 а1,25
а1,25


























































































R





 а
2,5
а
2,5
е
50t640k6d1=2040Е9




д
вг
Рисунок 5.4. Обозначение посадок подшипников качения на сборочных чертежах (а) и полей допусков на чертежах деталей: зубчатое колесо (б); крышка подшипника (в); отверстие в корпусе (г); вал пустотелый (д); распорная втулка (е)
5.1.3. Выбор посадок подшипников качения
Посадку подшипника качения на вал и в корпус выбирают в зависимости от следующих факторов: тип и размеры подшипника, условия эксплуатации, величина и характер действующих на него нагрузок, вид нагружения колец подшипника. Различают три вида нагружения колец подшипника: циркуляционное, местное и колебательное (рисунок 5.5).

Ц

















Ц












М















М







а б






























 М
Ц
М
Ц





























г
в
Рисунок 5.5. Виды нагружения колец подшипника качения (а, б) и эпюры напряжений при местном (в) и циркуляционном (г) нагружениях.
При циркуляционном нагружениикольцо воспринимает результирующую радиальную нагрузкуFrпоследовательно всей окружностью дорожки качения и также последовательно передает ее всей посадочной поверхности вала или корпуса (рисунок 5.5, а – наружное кольцо и рисунок 5.5, б – внутреннее кольцо).
Местное нагружение– это вид нагружения, при котором кольцо подшипника воспринимает постоянную по направлению результирующую Радиальную нагрузку одним и тем же ограниченным участком окружности дорожки качения и передает ее соответствующему ограниченному участку посадочной поверхности вала или корпуса (рисунок 5.5, а – внутреннее кольцо и рисунок 5.5, б – наружное кольцо).
При колебательном нагружениинеподвижное кольцо воспринимает равнодействующую силFrиFc(Fr– постоянная по величине,Fc– меньшая по величине, вращается) ограниченным участком окружности дорожки качения и передает ее ограниченному участку посадочной поверхности вала или корпуса. Равнодействующая силаFr + cне совершает полного оборота, а колеблется в пределах заданного угла поворота.
Эпюры напряжений при местном и циркуляционном нагружении показаны на рисунке 5.5, в, г. При колебательном нагружении эпюра напряжений подобна эпюре напряжений при циркуляционном нагружении, но она ограничивается углом поворота подвижного кольца подшипника.
При выборе посадок колец подшипников качения необходимо исходить из условия, что вращающееся кольцо должно быть смонтировано по посадке с натягом, а неподвижное кольцо – по посадке с зазором. Натяг вращающегося кольца подшипника должен быть минимальным, но исключающим возможность обкатки или проскальзывания кольца. Вращающимся является циркуляционно-нагруженное кольцо подшипника, неподвижным – местно- нагруженное кольцо. Для нормальной работы подшипника качения и выполнения им заданных функций после монтажа колец должен обеспечиваться рабочий (монтажный) зазор между телами качения и дорожками качения колец в установившемся режиме работы подшипника. Этот зазор должен быть оптимальным, что обеспечивает равномерное распределение нагрузки на все тела качения. При большом рабочем зазоре возникает большое радиальное биение и нагрузка воспринимается меньшим числом тел качения. При очень малом рабочем зазоре возможно заклинивание тел качения в процессе работы подшипника. Оптимальный зазор между телами качения и беговой дорожкой кольца обеспечивает наибольшую долговечность подшипника.
Выбор посадок подшипника качения начинают с кольца, которое испытывает циркуляционное нагружение. Посадку выбирают по интенсивности радиальной нагрузки, которая рассчитывается по формуле
PR = (Fr / b) · k1 · k2 · k3 , (5.1)
где PR – интенсивность радиальной нагрузки;
Fr– радиальная нагрузка на опору;
b– рабочая ширина посадочного места подшипника
b= В – 2r(см. рисунок 5.1.);
k1 – динамический коэффициент посадки, зависящий от характера нагрузки (при перегрузке до 150 % и умеренных толчках и вибрацииk1= 1,0; при перегрузке до 300 % сильных ударах и вибрацииk1= 1,8);
k2– коэффициент, учитывающий степень ослабления натяга при пустотелом вале или тонкостенном корпусе (для сплошных валовk2= 1,0);
k3– коэффициент неравномерности распределения радиальной нагрузкиFrмежду рядами тел качения в многорядных подшипниках (шариковых или роликовых), а также между сдвоенными подшипниками на одной опоре при наличии осевой нагрузкиFoна опору (для однорядных подшипников каченияk3= 1,0). Числовое значение коэффициентаk3 зависит от величины соотношения (Fo/Fr)ctgβ(гдеβ– угол контакта тел качения с беговой дорожкой качения наружного кольца и зависит от конструкции подшипника).
Величина коэффициента в зависимости от соотношения F0/Frможет быть принята из следующих рекомендаций (таблица 5.1).
Таблица 5.1
Значение коэффициента k3
|
F0/Fr |
до 0,2 |
0,2 – 0,4 |
0,4 – 0,6 |
0,6 – 1,0 |
свыше 1,0 |
|
k3 |
1,0 |
1,2 |
1,4 |
1,6 |
2,0 |
Из уравнения (5.1) видно, что с увеличением радиальной нагрузки увеличивается интенсивность радиальной нагрузки PR, а это влечет за собой увеличение необходимого натяга при посадке кольца подшипника.
По рассчитанному значению интенсивности радиальной нагрузки из таблицы выбирают посадку кольца подшипника, имеющего циркуляционное нагружение, а затем из таблицы рекомендуемых посадок для местно-нагруженных колец подшипника выбирают посадку для кольца, имеющего местное нагружение.
В случаях, когда динамический коэффициент k1 найти невозможно, посадку (натяг) для циркуляционно-нагруженного кольца рассчитывают по приближенной формуле
Nmin = 13 · Fr · N′ / [105 · (B – 2r)] , (5.2)
где Nmin – минимальный натяг;
Fr– радиальная нагрузка;
N′ − коэффициент, зависящий от серии подшипника (для легкой серииN′ =2,8; для средней серииN′ = 2,3; для тяжелой серииN′ = 2,0);
По найденной величине Nminвыбирают ближайшую посадку.
Во избежание разрыва колец подшипника наибольший натяг посадки не должен превышать допустимую величину (Nдоп), которая определяется по формуле
Nдоп = (11,4 · σд · N′ · d) / [(2N′ – 2) · 105] (мм), (5.3)
где σд – допустимое напряжение на растяжение (для подшипниковой стали σд = 400 МН/м2);
d – диаметр кольца подшипника.
При назначении больших натягов необходимо производить проверку на наличие радиальных зазоров и выход за пределы допустимых. При расчете посадок подшипников качения, работающих при повышенных температурах необходимо учитывать неравномерный нагрев и различие температурных коэффициентов расширения металлов внутреннего кольца подшипника и вала и выбирать посадку с натягом, тем большим, чем больше рабочая температура подшипника.
5.2. Взаимозаменяемость, методы и средства
контроля резьбовых соединений
5.2.1. Назначение и виды резьб
Резьбы широко распространены в машиностроении. В современных машинах и механизмах свыше 60 % деталей имеют резьбу, которая выполняет различные функции (крепежная резьба, кинематическая, ходовая и т. д.). По эксплуатационному назначению различают резьбы общего применения и специальные, которые предназначены для соединения деталей одного типа определенного механизма. Наиболее распространенными являются резьбы общего применения. К этой группе относятся резьбы: крепежные, кинематические, трубные (арматурные).
Крепежныерезьбы применяются для создания разъемных соединений деталей машин. По углу профиля эти резьбы бывают метрические и дюймовые. Основное требование к крепежным резьбам – обеспечить прочность соединения и сохранить плотность стыка в процессе длительной эксплуатации.
Кинематические резьбы. По профилю бывают трапецеидальные и прямоугольные. Применяются для ходовых винтов, винтов суппортов станков и столов измерительных приборов и т. д. Главное требование к кинематическим резьбам – обеспечение точного перемещения при наименьшем трении (для точных микрометрических приборов) и обеспечение плавности вращения и высокой нагрузочной способности (в прессах и домкратах).
Трубные (арматурные)резьбы. К ним относятся трубная цилиндрическая и коническая, коническая метрическая резьбы. Применяются для для трубопроводов и арматуры разного назначения. Общими требования к трубным и арматурным резьбам является надежность, долговечность и свинчиваемость без подгонки независимо изготовленных резьбовых деталей. При этом обязательно должны сохраняться эксплуатационные свойства соединений.
