3.2. Нормирование, методы и средства контроля отклонения формы и взаимного расположения поверхностей деталей

3.2.1. Классификация отклонений геометрических

параметров деталей

При анализе точности геометрических параметров деталей различают : номинальные поверхности (не имеющие отклонений формы и размеров), форма которых задана чертежом иреальные (действительные) поверхности, полученные в результате обработки или видоизменения в процессе эксплуатации детали.

Номинальное расположение поверхностиопределяется номинальными линейными и угловыми размерами между ними и базами или между рассматриваемыми поверхностями, если базы не даны.Реальное расположение поверхности(или профиля) определяется действительными линейными и угловыми размерами.База– поверхность или выполняющее ту же функцию сочетание поверхностей, ось, точка, принадлежащая заготовке или изделию и предназначенная для базирования.Профиль поверхности – линия пересечения (или контур сечения) поверхности с плоскостью или заданной поверхностью. Реальные поверхности и профили отличаются от номинальных.

Из-за отклонений действительной формы от номинальной, размеры деталей в различных сечениях, отличаются друг от друга (рисунок 3.6).

Отклонение текущего размера R(при определенном значении х) от номинального (постоянного размераR₀) определяется по формуле

∆R=R–R₀=f(φ), (3.8)

где f(φ) – функция, изображающая погрешность профиля.

Контур поперечного сечения должен удовлетворять условиям замкнутости, т. е. должно выполняться условие

f(φ+ 2π) =f(φ), (3.9)

где 2π – период функции полярного угла φ.

Контур сечения действительной поверхности можно характеризовать как совокупность гармонических составляющих отклонений профиля, определяемых спектрами фазовых углов и амплитуд, т. е. совокупностью отклонений с различными частотами. Для описания действительного профиля (контура сечения) поверхности используют разложение функции погрешности f(φ) в ряд Фурье, рассматривая отклонение ∆Rрадиуса-вектора как функцию полярного угла φ

_{к = ∞}

f(φ) =a₀/ 2 + ∑ (а_к·coskφ+b_k·sinkφ), (3.10)

^{к =1}

bZ

х

φе

Действительный

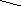
∆ФR₁ R профиль

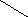
Номинальный профиль

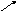
Шероховатость

bповерхности

R₀Прилегающая окружность

φ₁

D_min

∆D(отклонение размера)

D_max

Рисунок 3.6. Отклонение геометрических параметров различных порядков

где a_k,b_k – коэффициенты ряда Фурьеk–й гармоники;

k– порядковый номер составляющей гармоники;

a₀/2 – нулевой член разложения.

Ряд Фурье можно представить в виде

_k=∞

f(φ) = c₀ / 2 + ∑ c_k cos (kφ + φ_k), (3.11)

^k=1

где с_k – амплитуда k-й гармоники;

φ_k – начальная фаза.

При практическом применении формулы (3.11) число членом ряда Фурье ограничивают, т. е. пользуются тригонометрическим полиномом

_k=n

f(φ) =c₀/ 2 + ∑c_k cos(kφ+φ_k), (3.12)

^k=1

где n– порядковый номер высшей гармоники полинома.

Согласно теории Фурье, нулевой член разложения равен

_2π

c₀ / 2 = 1/2π∫f(φ)dφ, (3.13)

⁰

т. е. величина c₀/2 в общем случае является средней величиной функции f(φ) за период Т = 2π, определяемым расстоянием от базового уровня отсчета текущего размера до средней линии геометрических отклонений профиля. Таким образом, нулевой член разложения c₀/2 есть постоянная составляющая отклонения текущего размера.

Первый член разложения c₁ · cos(φ + φ₁) выражает несовпадение центра вращения действительного профиля с геометрическим центром номинального профиля (эксцентриситет е), т. е. отклонение расположения поверхности. Величина с₁ является амплитудой эксцентриситета е, φ₁– фаза эксцентриситета.

Члены ряда, начиная со второго и до k=p, т. е.

_k=p

∑ c_k cos(kφ + φ_k), (3.14)

^k=2

образуют спектр отклонений, характеризующих погрешности формы в поперечном сечении. При этом второй член ряда Фурье с₂cos (kφ + φ₂) выражает овальность, третий член с₃cos (kφ + φ₃) – огранку с трехвершинным про-филем и т. д. Последующие члены ряда после k > p выражают волнистость. При достаточно большом количестве членов ряда получают высокочастот-ные составляющие, соответствующие шероховатости поверхности.

Аналогичным образом могут представляться отклонения контура цилиндрической поверхности в продольном сечении. При этом условие замкнутости контура отсутствует

f(z) ≠f(z+l), (3.15)

где z– переменная величина, отсчитываемая вдоль оси цилиндра, при этом

0 ≤ z ≤ l;

l – длина детали.

В цилиндрической системе координат и с учетом координат R,zи φ, а также приняв условно период Т = 2l, отклонения контура реальной цилиндрической детали в продольном направленииf(z) можно представить в виде тригонометрического полинома

_k=p

f(z) = c₀/2 + ∑ c_k · sin(kπ/2l) · z, (3.16)

^k=1

где k– порядковый номер члена разложения.

При k= 1 первый член полинома имеет вид

f(z) =c₁·sin(π/2l)z, (3.17)

При z= 0f₁(z) = 0, а приz=lf₁(z) =c₁.

Первый член разложения характеризует угол наклона образующей цилиндра, т. е. конусообразность. Второй член разложения имеет вид

f₂(z) =c₂·sin(π/l)z, (3.18)

и характеризует выпуклость цилиндрического контура в продольном сечении (бочкообразность). Этот же член ряда Фурье при сдвиге фазы на величину π/2, имеет вид

f₂(z) =c₂·sin[(π/l)z– (π/2)] =c₂·cos(π/l)z, (3.19)

и выражает вогнутость цилиндрического контура (седлообразность).

Отклонения геометрических параметров можно классифицировать и более укрупнённо: отклонение размера (∆Dна рисунке 3.6) относят к отклонениям нулевого порядка; отклонение расположения поверхностей (е) – к отклонениям 1-го порядка; отклонение формы поверхности (∆Ф на рисунке 3.6) – к отклонениям 2-го порядка; волнистость поверхности – к отклонениям 3-го порядка; шероховатость поверхности – к отклонениям 4-го порядка.