4.2. Методы расчета размерных цепей и задачи,

решаемые при расчете размерных цепей

Существуют два метода расчета размерных цепей: метод расчета обеспечивающий полную взаимозаменяемость и метод расчета обеспечивающий неполную взаимозаменяемость.

При решении размерных цепей методом полной взаимозаменяемости существуют три способа решения: способ “максимума – минимума”; способ равных допусков; способ равной точности.

При решении размерных цепей методом неполной взаимозаменяемости существую также три способа: способ групповой взаимозаменяемости (селективная сборка); способ пригонки; способ регулирования.

Первая задача. Определение номинального размера и допуска (предельных отклонений) замыкающего звена по заданным номинальным размерам и предельным отклонениям составляющих звеньев. Такая задача обычно возникает при необходимости проверки соответствия допуска замыкающего звена допускам, составляющих размеров, проставленных на чертеже, т. е. это проверочный расчет.

Вторая задача. Определение допусков и предельных отклонений составляющих звеньев размерной цепи по заданным номинальным размерам всех размеров размерной цепи и заданными предельными размерами замыкающего звена. Такая задача решается при проектном расчете размерной цепи.

4.3. Расчет размерных цепей методом

полной взаимозаменяемости

4.3.1. Расчет размерных цепей способом “максимума – минимума”

Данный метод расчета размерных цепей применяется в случаях, когда для сборочной единицы необходимо обеспечить полную взаимозаменяемость. Способом “максимума – минимума” решается первая задача. Расчет ведется в предположении, что все звенья размерной цепи одинаково вероятно могут принимать как максимальные, так и минимальные размеры. Данный метод обеспечивает заданную точность сборки без какого – либо подбора или подгонки деталей.

Рассмотрим расчет методом “максимума – минимума”, на примере размерной цепи, состоящей из mзвеньев (рисунок 4.2).

В общем случае при nувеличивающих иpуменьшающих звеньях номинальный размер замыкающего звена А₀определяется из уравнения

_{n p}

А₀ = ∑ А_{i ув.} – ∑ А_{j ум.} , (4.1)

^{i=1 J =1}

где А_{i ув.} – размер i – го увеличивающего звена размерной цепи;

А _{j ум.}– размерj– го уменьшающего звена размерной цепи;

n– количество увеличивающих звеньев размерной цепи;

p– количество уменьшающих звеньев размерной цепи.

А₁А₃ А₆ А₇

А₂ А₄А₅ А₈А₉

А₀

Рисунок 4.2. Расчетная схема размерной цепи

Следует отметить, что деталь по замыкающему размеру не обрабатывают. Этот размер получается в результате обработки детали по другим размерам, которые связаны с этим размером. В сборочных размерных цепях замыкающий размер определяется последовательностью сборки.

Более важными являются предельные размеры замыкающего звена, так как составляющие размерную цепь звенья изменяются в установленных допусками пределами. Предельные размеры замыкающего звена определяются из уравнений

_{n p}

А_0max = ∑ А_{imax ув.} – ∑ А_{jmin ум.} , (4.2)

^{i=1 J =1}

_{n p}

А_0min = ∑ А_{imin ув.} – ∑ А_{jmax ум.} , (4.3)

^{i=1 J =1}

Учитывая, что разность между предельными размерами есть допуск, вычитая почленно равенство (4.3) из равенства (4.2) получим

_{n p}

ТА₀ = ∑ ТА_{i ув.} – ∑ ТА_{j ум.} (4.4)

^{i=1 J =1}

_n

ТА₀= ∑ ТА_i (4.5)

ⁱ⁼¹

Кроме того, допуск замыкающего звена размерной цепи можно определить как разность предельных размеров этого звена по уравнению

ТА₀= А_0max– А_0min. (4.6)

Если принять общее число звеньев размерной цепи равным m, а число составляющих звеньевm– 1, то допуск замыкающего звена равен

Иногда при расчете размерных цепей целесообразно определять не величины допуска замыкающего звена, а величины его отклонений. Расчет ведут по формулам

_{n p}

Es (А₀) = ∑ Es (А_i)_ув. – ∑ Ei (А_j)_ум., (4.7)

^{i=1 J =1}

_{n p}

Ei (А₀) = ∑ Ei (А_i) _ув. – ∑ Es (А_j) _ум. , (4.8)

^{i=1 J =1}

где Es – верхнее отклонение размера размерной цепи;

Ei– нижнее отклонение размера размерной цепи.

Иногда при расчетах удобно пользоваться координатой середины поля допуска Ec(А_i) и половиной поля допускаTA_i/2 (рисунок 4.3)..

Tai/2

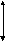
Ec(Ai) Es(Ai)

0 0

TAi Ei(Ai)

номинальный

размер

Рисунок 4.3. Схема для определения координаты середины поля допуска звена размерной цепи

Для любого составляющего звена размерной цепи предельные отклонения можно определить по формулам

Es(Ai) = Ec(Ai) + TАi/2, (4.9)

Ei(Ai) = Ec(Ai) – TАi/2, (4.10)

где Eс – координата середины поля допуска i – го звена размерной цепи;

TА_i/2 – половина поля допускаi– го звена размерной цепи.

Величины отклонений EsиEiопределяются по таблицам стандартов ГОСТ 25346 – 89 (СТ СЭВ 145 – 88).

Аналогично определяются предельные отклонения и для замыкающего звена размерной цепи

Es(A₀) = Ec(A₀) + TА₀/2, (4.11)

Ei(A₀) = Ec(A₀) – TА₀/2, (4.12)

Используя уравнения (4.9), (4.10), (4.11) и (4.12) можно определить предельные размеры замыкающего звена по формулам

_{n p}

A₀ + Es (A₀) = ∑[A_i + Es(A_i)]_ув. – ∑[A_j + Ei(A_j)]_ум., (4.13)

^{i=1 j=1}

_{n p}

A₀ + Ei (A₀) = ∑[A_i + Ei(A_i)]_ув. – ∑[A_j + Es(A_j)]_ум., (4.14)

^{i=1 j=1}

Подставив в уравнения (4.7) и (4.8) значения предельных отклонений, выраженных через координату середины поля допуска по уравнениям (4.11) и (4.12) получим уравнения для расчета предельных отклонений замыкающего звена через координаты середин полей допусков

_{n p}

Ec (A₀) + TA₀/2 = ∑ [Ec(A_i) + TA_i/2]_ув. – ∑ [Ec(A_j) – TA_j/2] , (4.15)

^{i=1 j=1}

_{n p}

Ec (A₀) – TA₀/2 = ∑ [Ec(A_i) – TA_i/2]_ув. – ∑ [Ec(A_j) + TA_j/2] , (4.16)

^{i=1 j=1}

Сложив почленно уравнения (4.15) и (4.16) и разделив полученную сумму на 2, получим выражение для определения координаты середины поля допуска замыкающего звена размерной цепи

_{n p}

Ec(A₀) = ∑ Ec(A_i)_ув. – ∑ Ec(A_j)_ум. (4.17)

^{i=1 j=1}

Совпадение результатов расчетов параметров замыкающего звена, выполненных по разным уравнениям, указывает на правильность расчета размерной цепи.