[Править]Определение через разложение по первой строке

Схема расчета определителя матрицы   .

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы   детерминант определяется как

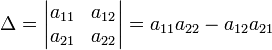
Для матрицы   определитель задаётся рекурсивно:

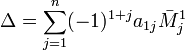,    где   — дополнительный минор к элементу  . Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы   такова:

Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):

Доказательство  [показать]

Также справедливо и аналогичное разложение по любой строке (столбцу):

Доказательство  [показать]

Обобщением вышеуказанных формул является разложение детерминанта по Лапласу (Теорема Лапласа), дающее возможность вычислять определитель по любым k строкам (столбцам):

[Править]Определение через перестановки

Для матрицы   справедлива формула:

,

где   — перестановка чисел от 1 до  ,   — число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка  . Таким образом, в определитель войдёт   слагаемых, которые также называют «членами определителя». Важно заметить, что во многих курсах линейной алгебры это определение даётся как основное.

[Править]Альтернативные методы вычисления

• Метод конденсации Доджсона, основанный на рекурсивной формуле:

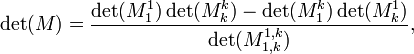 где   матрицы, получающиеся из исходной вычёркиванием соответствующих строк и столбцов.

[Править]Свойства определителей

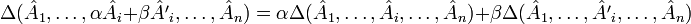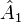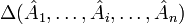• Определитель — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам):   , где   и т. д. — строчки матрицы,   — определитель такой матрицы.

• При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится.

• Если две строки (столбца) матрицы совпадают, то её определитель равен нулю.

• Если две (или несколько) строки (столбца) матрицы линейно зависимы, то её определитель равен нулю.

• Если переставить две строки (столбца) матрицы, то её определитель умножается на (-1).

• Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

• Если хотя бы одна строка (столбец) матрицы нулевая, то определитель равен нулю.

• Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю.

• Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

• Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей (cм. также формулу Бине-Коши).

• С использованием индексной нотации определитель матрицы 3×3 может быть определён с помощью символа Леви-Чивита из соотношения:

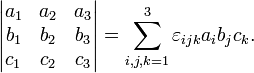
[Править]Алгоритмическая реализация

• Наивные методы для вычисления определителя могут быть основаны непосредственно на его определении, как суммы по перестановкам, или на разложении Лапласа по определителям меньшего порядка. Однако такие методы очень неэффективны, так как требуют О(n!) операций для вычисления определителя  -го порядка.

• Один из более быстрых методов заключается в простой модификации метода Гаусса. Следуя методу Гаусса, произвольную матрицу 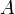  можно привести к ступенчатому виду(Верхнетреугольная матрица), используя лишь две следующие операции над матрицей — перестановку двух строк и добавление к одной из строк матрицы другой строки, умноженной на произвольное число. Из свойств определителя следует, что вторая операция не изменяет определителя матрицы, а первая лишь меняет его знак на противоположный. Определитель матрицы, приведённой к ступенчатому виду, равен произведению элементов на её диагонали, так как она является треугольной, поэтому определитель исходной матрицы равен:

где   — число перестановок строк, выполненных алгоритмом, а   — ступенчатая форма матрицы  , полученная в результате работы алгоритма. Сложность этого метода, как и метода Гаусса, составляет  .

• Определитель можно вычислить, зная LU-разложение матрицы. Если 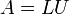 , где   и   — треугольные матрицы, то 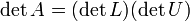 . Определитель треугольной матрицы равен просто произведению её диагональных элементов.

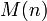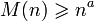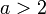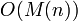• Если доступен алгоритм, выполняющий умножение двух матриц порядка   за время  , где  , для некоторого  , то определитель матрицы порядка  может быть вычислен за время  .^[1] В частности это означает, что, используя для умножения матриц алгоритм Копперсмита — Винограда, определитель можно вычислить за время  .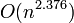

   Алгебраические дополнения 

     Алгебраическое дополнение элемента   определителя   - определитель   где   - минор элемента  .

     Разложение определителя 

     По элементам i-й строки:

     По элементам j-го столбца:

     Например, при n = 4 разложение по первой строке

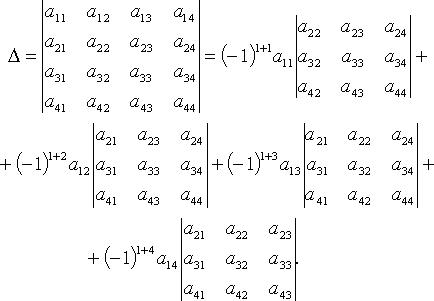
     Свойства определителя 

     1. 

     2. Если все элементы какой-нибудь строки (столбца) определителя равны нулю, то определитель равен нулю.

     3. Если матрица B получена из матрицы A перестановкой двух каких-либо ее строе (столбцов), то 

     4. Общий множитель всех элементов произвольной строки (столбца) определителя можно вынести за знак определителя.

     5. Определитель, содержащий две пропорциональные строки (столбца), равен нулю.

     6. Пусть   - квадратная матрица порядка n; k - фиксированное натуральное число:   - матрицы, которые получаются из A заменой ее k-й строки (столбца) соответственно строками (столбцами)     Тогда 

     7. Определитель не меняется от прибавления к какой-либо его строке (столбцу) другой его строки (столбца), умноженной на произвольное число.

     8. Если какая-либо строка (столбец) определителя есть линейная комбинация других его строк (столбцов), то определитель равен нулю.

     9. 

Обратная матрица

Обратной матрицей называется матрица, которая при умножении как справа, так и слева на данную матрицу дает единичную матрицу. Обозначим обратную матрицу к матрице А через  , тогда согласно определению получим:

где Е – единичная матрица. Квадратная матрица называется неособенной (невырожденной), если ее определитель не равен нулю. В противном случае она называется особенной (вырожденной) или сингулярной.  Имеет место теорема: всякая неособенная матрица имеет обратную матрицу. Операция нахождения обратной матрицы называется обращением матрицы. Рассмотрим алгоритм обращения матрицы. Пусть дана неособенная матрица n-го порядка:

где Δ = det A ≠ 0.

Алгебраическим дополнением элемента матрицы n -го порядка А называется взятый с определенным знаком определитель матрицы (n –1)-го порядка, полученной вычеркиванием i-ой строки и  j-го столбца матрицы А: 

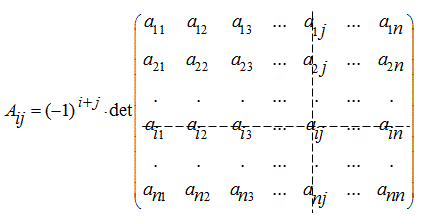
Составим так называемую присоединенную матрицу:

где – алгебраические дополнения соответствующих элементов матрицы А. Заметим, что алгебраические дополнения элементов строк матрицы А размещаются в соответствующих столбцах матрицы Ã, то есть одновременно производится транспонирование матрицы. Разделив все элементы матрицы Ã на Δ – величину определителя матрицы А, получим в результате обратную матрицу :

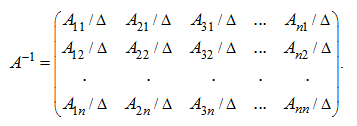
Отметим ряд особых свойств обратной матрицы: 1) для данной матрицы А ее обратная матрица    является единственной; 2) если существует обратная матрица  , то правая обратная и левая обратная матрицы совпадают с ней; 3) особенная (вырожденная) квадратная матрица не имеет обратной матрицы. Основные свойства обратной матрицы: 1) определитель обратной матрицы и определитель исходной матрицы являются обратными величинами; 2) обратная матрица произведения квадратных матриц равна произведениюобратных матриц сомножителей, взятому в обратном порядке:

3) транспонированная обратная матрица равна обратной матрице от данной транспонированной матрицы:

П р и м е р .  Вычислить матрицу, обратную данной:

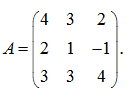
Р е ш е н и е . Определитель матрицы  А равен:

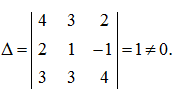
Следовательно, матрица  А неособенная. Присоединенная матрица Ã имеет вид:

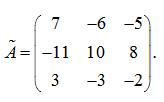
Разделив все элементы присоединенной матрицы Ã на Δ = 1, получим обратную матрицу  :

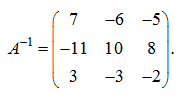
Проверим, что действительно, 

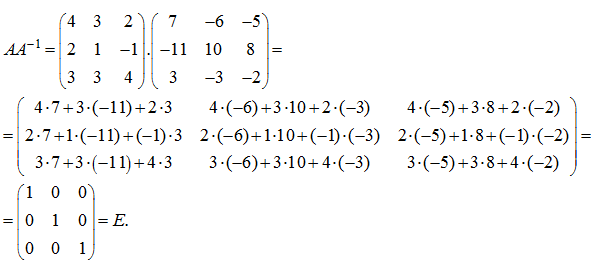
Таким образом, найденная матрица  является обратной для заданной матрицы А.

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод.

[править]Описание метода

Для системы   линейных уравнений с   неизвестными (над произвольным полем)

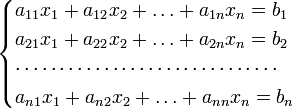
с определителем матрицы системы  , отличным от нуля, решение записывается в виде

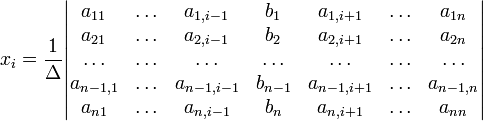
(i-ый столбец матрицы системы заменяется столбцом свободных членов). В другой форме правило Крамера формулируется так: для любых коэффициентов c₁, c₂, …, c_n справедливо равенство:

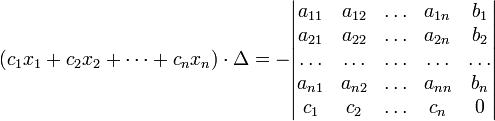
В этой форме формула Крамера справедлива без предположения, что   отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы   и  , либо набор   состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

[править]Пример

Система линейных уравнений:

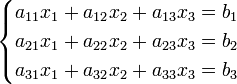
Определители:

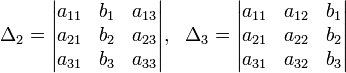
Решение:

Пример:

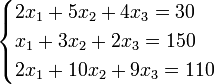
Определители:

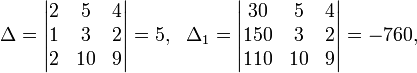
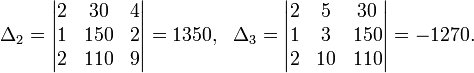
[править]Вычислительная сложность

Метод Крамера требует вычисления   определителей размерности  . При использовании метода Гаусса для вычисления определителей, метод имеет временную сложность порядка  , что хуже, чем если бы метод Гаусса напрямую использовался для решения системы уравнений. Поэтому метод считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностью  , сравнимой со сложностью метода Гаусса.^[1]

Теорема Безу. Если многочлен   разделить на двучлен x - a, то в остатке получим число R, равное значению данного многочлена при x = a, т. е. R = P_n(a).

Схема сокращенного деления многочлена на двучлен. При делении многочлена  , расположенного по убывающим степеням x, на двучлен x - a применяется метод сокращенного деления, называемый схемой Горнера.

Имеют место следующие формулы для нахождения коэффициентов частного b₁, b₂, ..., b_n-1 и остатка R:

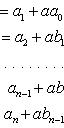
Практически вычисление коэффициентов частного Q_n-1(x) и остатка R проводится по следующей схеме (схеме Горнера).

Пусть требуется разделить многочлен   на двучлен x - a.

Значение a двучлена, коэффициенты многочлена (b_n-1, b_n-2, ..., b₀) и остаток запишем в следующей форме:

an	an-1	an-2	...	a1	a0
bn-1 = an	bn-2 = an-1 + abn-1	bn-3 = an-2 + abn-2	...	b0 = a1 + ab1	R = a0 + ab0

Отсюда записываем частное

если R = 0, и результат деления

 или  ,

если R ≠ 0.