[Править]Примеры

Следующие пять многочленов демонстрируют некоторые элементарные свойства неприводимых многочленов:

,

,

,

,

.

Над кольцом   целых чисел, первые два многочлена — приводимые, последние два — неприводимые. (Третий вообще не является многочленом над целыми числами).

Над полем   рациональных чисел, первые три многочлена являются приводимыми, двое других — неприводимыми.

Над полем   действительных чисел, первые четыре многочлена — приводимые, но   является неприводимым. В поле действительных чисел неприводимыми являются линейные многочлены и квадратичные многочлены без действительных корней. Например разложение многочлена   в поле действительных чисел имеет вид  . Оба множителя в данном разложении являются неприводимыми многочленами.

Над полем   комплексных чисел, все пять многочленов — приводимые. Фактически, каждый отличный от константы многочлен   над   может быть разложен на множители вида:

где   — степень многочлена,   — старший коэффициент,   — корни  . Поэтому единственными неприводимыми многочленами над   являются линейные многочлены (основная теорема алгебры).

[править]Конечные поля

Многочлены с целочисленными коэффициентами, которые являются неприводимыми над полем   могут быть приводимыми над конечным полем. Например, многочлен  является неприводимым над  , но над полем   из двух элементов мы имеем:

Симметрический многочлен

[править]

Материал из Википедии — свободной энциклопедии

Симметри́ческий многочле́н — многочлен от n переменных  , не изменяющийся при всех перестановках входящих в него переменных.

[править]Примеры

• Дискриминант — многочлен вида 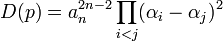 , где 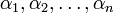  — корни некого многочлена от одной переменной:  .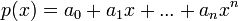

• Степенные суммы — суммы одинаковых степеней переменных, то есть 

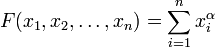
• Основные симметрические многочлены — многочлены вида

определённые для  , то есть такие:

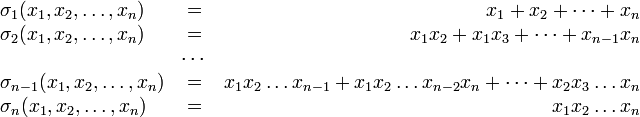
[править]Основная теорема теории симметрических многочленов

Основная теорема теории симметрических многочленов гласит, что любой симметрический многочлен может быть представлен единственным образом в виде многочлена от основных симметрических многочленов.

Алгебраическое число

[править]

Материал из Википедии — свободной энциклопедии

Алгебраи́ческое число́ над полем   — элемент алгебраического замыкания поля  , то есть корень многочлена (не равного тождественно нулю) с коэффициентами из  .

Если поле не указывается, то предполагается поле рациональных чисел, то есть  , в этом случае поле алгебраических чисел обычно обозначается  . Поле   являетсяподполем поля комплексных чисел.

Эта статья посвящена именно этим «рациональным алгебраическим числам».

[Править]Связанные определения

• Комплексное число, не являющееся алгебраическим, называется трансцендентным.

• Целыми алгебраическими числами называются корни многочленов с целыми коэффициентами и со старшим коэффициентом единица.

• Есл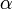и   — алгебраическое число, то среди всех многочленов с рациональными коэффициентами, имеющих   своим корнем, существует единственный многочлен наименьшей степени со старшим коэффициентом, равным  . Такой многочлен автоматически является неприводимым, он называется каноническим, или минимальным, многочленом алгебраического числа  . (Иногда каноническим называют многочлен, получающийся из минимального домножением на наименьший общий знаменатель его коэффициентов, то есть многочлен с целыми коэффициентами)

  • Степень канонического многочлена   называется степенью алгебраического числа  .

  • Другие корни канонического многочлена   называются сопряжёнными к  .

  • Высотой алгебраического числа   называется наибольшая из абсолютных величин коэффициентов в неприводимом и примитивном многочлене с целыми коэффициентами, имеющем   своим корнем.