Подстановка

Определение 1. Произвольное взаимно однозначное отображение множества первых   натуральных чисел называетсяподстановкой¹⁾  -го порядка.

Замечание 1. Часто подстановки называют перестановками.

Обычно подстановку   изображают следующим образом:  , что задает образы всех элементов:  ,   и так далее. Также используют запись  .

Пример 1. Подстановку   можно записать также в виде  , так как в обоих случаях мы имеем отображение  ,  ,  .

Определение 2. Элемент   подстановки   называется действительно перемещаемым, если  .

Пример 2. В подстановке   два действительно перемещаемых символа: 1 и 3.

Операция умножения на подстановках определяется как композиция отображений, причем знак композиции   обычно опускают

.

Транспозиции и циклы

Определение 3. Циклической подстановкой²⁾, или циклом³⁾ называется такая подстановка  , что при повторении ее достаточное число раз всякий из действительно перемещаемых ею символов может быть переведен в любой другой из этих символов. Для обозначения цикла используют запись  , где   — число действительно перемещаемых символов подстановки, которое называется длиной цикла⁴⁾.

Пример 3. В подстановке

действительно перемещаемыми символами являются 1, 3, 4, 5, 6. Выберем любой из них, например, 3.  ,  . Поэтому цикл можно записать как  .

Определение 4. Циклы называются независимыми⁵⁾, если они не имеют общих действительно перемещаемых символов.

Предложение 1. Любая подстановка   из   может быть разлжена в произведение попарно независимых циклов. Такое представление определено однозначно с точностью до порядка перемножения циклов.

Пример 4.   — разложение подстановки в произведение попарно независимых циклов.

Определение 5. Цикл длины 2 называется транспозицией⁶⁾.

Предложение 2. Каждая подстановка может быть представлена в виде произведения транспозиций.

Доказательство.

В отличие от представления в произведение попарно независимых циклов, представление в виде произведения транспозиций может не быть единственным.

Пример 5. Подстановка   может быть разложена в произведение транспозиций   или  .

Четность подстановки

Определение 6. Пусть   — разложение подстановки   в произведение транспозиций. Тогда число   называетсязнаком⁷⁾(четностью) подстановки  . Подстановка называется четной⁸⁾, если   и нечетной⁹⁾ в противном случае.

Предложение 3. Четность подстановки не зависит от способа разложения подстановки в произведение транспозиций.

Предложение 4. Для двух подстановок   и   четность их произведения равна произведению четностей:

.

Доказательство.

Предложение 5. Пусть   — цикл длины  . Тогда его четность равна  .

Доказательство.

Определение 7. Пусть   — разложение подстановки в произведение независимых циклов длин  . Число  называется декрементом¹⁰⁾ подстановки  .

Предложение 6. Пусть   — разложение подстановки в произведение независимых циклов длин  . Тогда четность подстановки  вычисляется по формуле

.

Доказательство.

Пример 6. Любая транспозиция — это нечетная подстановка. Подстановка из примера 4 нечетная, так как декремент   — нечетное число.

Пример 7. Любая подстановка, в разложении которой на независимые циклы все циклы имеют нечетные длины  , четна, так как ее декремент — это сумма   четных чисел  .

-группа

Группа, все элементы в которой имеют порядок, равный некоторой степени простого числа   (не обязательно одинаковой у всех элементов). Также говорят о примарной группе 

Аддитивная группа кольца

Группа, элементами которой являются все элементы данного кольца, а операция совпадает с операцией сложения в кольце.

Группа

Непустое множество   с заданной на нём ассоциативной бинарной операцией  , при которой в   имеется нейтральный элемент  , то есть для всех  выполнено  , и для каждого элемента   есть обратный элемент  , такой, что  .

Системы линейных уравнений

Если в системе (5.40) все функции fi линейны по пере-менным y1,y2,...,yn, то она называется линейной. В этом случае её можно переписать в виде

{y′1=a11(x)y1+a21(x)y2+...+an1(x)yn+b1(x),y′2=a12(x)y1+a22(x)y2+...+an2(x)yn+b2(x),..........................................................................y′n=a1n(x)y1+a2n(x)y2+...+ann(x)yn+bn(x).

5.42

Обозначая матрицу системы через A(x), а вектор (b1(x),b2(x),...,bn(x))T через b(x), систему (5.42) можем переписать в матричной форме

 y′=A(x)y+b(x). (5.42а)

Будем, по возможности, пользоваться матричной формой записи. Если b(x)=0, то получаем соответствующую систему однородных уравнений

y′=A(x)y.

5.43

Для систем линейных уравнений строится теория, полностью эквивалентная теории линейных уравнений порядка n. В частности, справедлива теорема о наложении решений и её следствия. В том числе и теорема о том, что множество решений однородной системы (5.43) образует линейное подпространство в пространстве дифференцируемых вектор-функций. Сформулируем и по возможности докажем эти результаты.

Так же, как для векторов [1,2] и систем скалярных функций, для систем вектор-функций вводятся понятия их линейной зависимости и линейной независимости.

Определение. Система вектор-функций y1,y2,...,ym называется линейно зависимой на отрезке [a,b], если существуют числа α1,α2,...,αm, не все из которых равны нулю, такие, что

 α1y1+α2y2+...+αmym=∑i=1mαiym=0 

всюду на [a,b], и линейно независимой, если такого ненулевого набора не существует.

Рассмотрим совокупность вектор-функций y1,y2,...,yn. Определитель, составленный из их координат,

 W(x)=|y11y21…yn1y12y22…yn2…………y1ny2n…ynn| 

называется определителем Вронского, или вронскианом системы вектор-функций y1,y2,...,yn.

Так же, как и для систем скалярных функций, определитель Вронского системы вектор-функций служит индикатором её линейной зависимости или линейной независимости.

Теорема. Если система вектор-функций линейно зависима, то её определитель Вронского W(x) равен нулю.

Доказательство аналогично соответствующему доказательству для систем векторов [1,2] и систем скалярных функций, приведённому в п. 5.2.3. Предлагается сделать это самостоятельно.

Теорема. Если y1,y2,...,yn - линейно независимая совокупность решений однородной системы уравнений y′=A(x)y, то её определитель Вронского W(x) отличен от нуля для всех x∈[α,β].

Доказательство аналогично соответствующему доказательству для систем скалярных функций, приведённому в п. 5.2.3. Предлагается доказать эту теорему самостоятельно.

Удостоверимся в существовании базиса в пространстве решений системы уравнений y′=A(x)y.

Теорема. Для любой однородной системы линейных дифференциальных уравнений y′=A(x)y порядка n существует система n линейно независимых решений этого уравнения.

Доказательство. Возьмём матрицу

(q11q21…qn1q12q22…qn2…………q1nq2n…qnn)

5.44

с определителем, отличным от нуля. Тогда строки и столбцы этой матрицы линейно независимы. Найдём такие решения yj(x),j=1,2,...n, системы уравнений y′=A(x)y, чтобы выполнялись соотношения ykj(x0)=qkj,k=1,2,...n. По теореме существования и единственности такой набор решений существует. Найденная система решений линейно независима, так как её определитель Вронского в точке x0 совпадает с определителем матрицы (5.44). Теорема доказана.

Матрицу (5.44) можно взять единичную.

Теорема (о виде общего решения однородной системы линейных дифференциальных уравнений). Если y1,y2,...,yn - линейно независимая совокупность решений однородной системы уравнений y′=A(x)y, то любое решение этой системы есть линейная комбинация решений y1,y2,...,yn, то есть

 y(x)=∑j=1nCjyj(x) 

и, следовательно, y1,y2,...,yn - базис пространства решений системы уравнений y′=A(x)y.

Доказательство. Нам нужно доказать, что для любого набора начальных данных (5.41) (y1(x0),y2(x0),...,yn(x0))T=  =(y10,y20,...,yn0)T можно подобрать константыCj, j=1,2,...,n, так, что соответствующее решение y(x) удовлетворяет (5.41). Потребовав, чтобы решение y(x) удовлетворяло условиям (5.41), получим систему линейных алгебраических уравнений

 ∑j=1nCjykj(x0)=yk(x0)=yk0,  k=​​​ 1,2, ..., n, 

определитель которой W(x0)≠0 и поэтому существует единственное решение этой системы.

Таким образом, нами показано, что подпространство решений однородной системы линейных дифференциальных уравнений конечномерно.

Определение. Любой базис пространства решений однородной системы линейных дифференциальных уравнений  n -го порядка называется фундаментальной системой решений этой системы уравнений.

Так же, как и в линейной алгебре, имеет место следующий результат.

Теорема (о виде общего решения линейного неоднородного дифференциального уравнения). Общее решение yон линейной неоднородной системы дифференциальных уравнений y′=A(x)y+b(x) есть сумма общего решения yоо соответствующей однородной системы уравнений y′=A(x)y и какого либо частного решенияyчн неоднородной системы уравнений, то есть yон(x)=yоо(x)+yчн(x).

Доказательство. Пусть yчн(x) какое-нибудь фиксированное частное решение неоднородной системы линейных уравнений y′=A(x)y+b(x). Нам нужно показать, что для любого набора начальных данных (y1(x0),y2(x0),...,yn(x0))T=  =(y10,y20,...,yn0)T можно подобрать константы Cj, j=1,2,...,n, так, что решениеy(x)=∑j=1nCjyj(x)+yчн(x), где y1,y2,...,yn - фундаментальная система решений соответствующей однородной системы уравнений y′=A(x)y, удовлетворяет этому набору начальных данных. Потребовав, чтобы данное решение удовлетворяло начальным условиям, получим систему линейных алгебраических уравнений

 ∑j=1nCjykj(x0)+(yчн)k(x0)=yk(x0)=yk0,  k=1,2, ... , n,

или, что то же самое,

 ∑j=1nCjykj(x0)=yk0−(yчн)k(x0),  k=1,2, ... , n,

определитель которой W(x0)≠0 и поэтому существует единственное решение этой системы. Теорема доказана.

Однородные системы

Однородной системой линейных уравнений называется система вида:

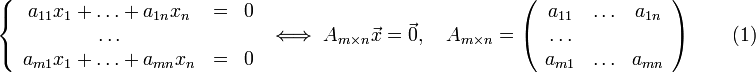
Нулевое решение   системы (1) называется тривиальным решением.

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.

Решения однородной системы обладают свойством линейности:

Сформулируем теорему, которая позволит дать основное определение:

Пусть дана однородная система (1), тогда набор векторов   размера   называется фундаментальной системой решений (ФСР) (1), если:

•  — решения системы (1);

•  линейно независимы;

• .

[Править]Пример

Решим систему

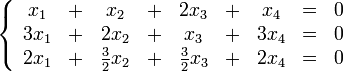
Перепишем её в матричном виде:

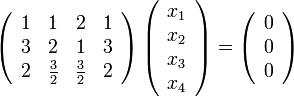
Путём элементарных преобразований над строками приведём её основную матрицу к ступенчатому виду:

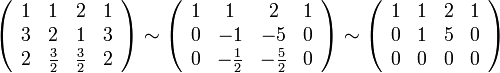
Таким образом ранг системы (ранг её основной матрицы) равен двум. Это значит, что существует   линейно независимых решения системы.

Перепишем полученную систему в виде уравнений:

Возьмём   и   в качестве главных переменных. Тогда:

Подставим по очереди единицы в качестве одной из свободных переменных:   и  .

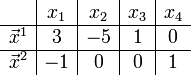
Тогда общее решение рассматриваемой системы может быть записано так:

,

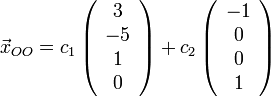а вектора 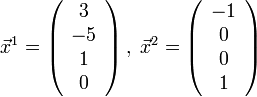  составляют фундаментальную систему решений.

[Править]Неоднородные системы

Неоднородной системой линейных уравнений называется система вида:

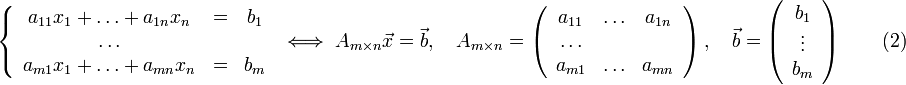
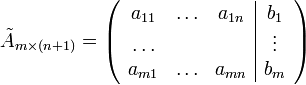 — её расширенная матрица.

[Править]Пример

Решим систему

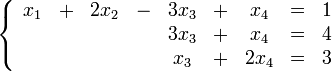
Преобразуем её к

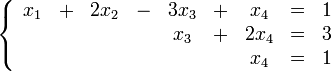
Тогда переменные   и   обязательно будут главными, возьмём также   в качестве главной.

Заметим, что   является частным решением.

Составим однородную систему:

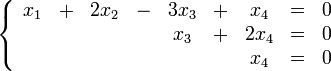
Тогда, подставив единицу в качестве свободной переменной  , получим ФСР однородной системы:

Общее решение системы может быть записано так:

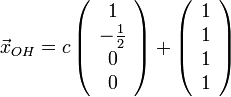
Ранг системы векторов. Базис системы векторов

Теорема. Если система векторов   линейно-зависима, то она эквивалентна системе 

Доказательстово.  Действительно, пусть  одновременно неравные нулю числа такие, что  . Предположим, что  _S  0  , разделим эту сумму на   _S, получим:   или

 , где    .

Заменим систему векторов   эквивалентной системой   с помощью следующего элементарного преобразования:

  при   и   . Тогда  вектор  . Поменяв местами векторы   и     получим систему вида   .  Что и требовалось доказать.

Следствие. Произвольную систему векторов   элементарными преобразованиями можно привести к системе вида    , где

 линейно независимая система векторов.

Число    будем называть  рангом  системы векторов  , а систему

 – базисом  системы векторов  .

Отметим, что ранг системы векторов   не зависит от конкретной цепочки элементарных преобразований.

Алгоритм Гаусса для нахождения ранга и базиса системы векторов

 

Пусть  – система векторов из  .

...............

Запишем систему в виде таблицы (матрицы):

                                   

 

Эта таблица имеет   строк и   столбцов,  – размерность матрицы. Наша цель - элементарными преобразованиями строк привести матрицу к верхней треугольной форме

                                   

Эта матрица соответствует системе векторов   эквивалентной системе  .  Ненулевые векторы системы   линейно независимы и образуют базис системы векторов  . Число ненулевых  векторов в системе   - ранг системы векторов   .

 1 шаг. Рассмотрим первый ненулевой столбец матрицы. Пусть это будет её первый столбец. Просматривая элементы сверху вниз, найдем элемент  , затем переставим первую  строку со строкой с индексом  . 

Получим новую матрицу, которую обозначим также

                                   

Мы поменяли значения переменных строки 1 и строки с индексом  . В этой матрице  .

2 шаг. Разделим первую строку  на   (умножим на  ). Получим: матрицу вида

                                         

3 шаг.  В цикле от   до    по индексу строки   сделаем следующее : от    -ой  строки отнимаем 1 строку, умноженную на  . В результате получим матрицу вида  

                                  

Теперь наше внимание сосредоточим на матрице, полученной из данной вычеркиванием  первой строки и первого столбца.

                                  

 

4 шаг.  Рассмотрим первый  столбец этой матрицы (элементы  ). Если все элементы столбца равны нулю,  то переходим к следующему столбцу, пока не найдем первый ненулевой столбец этой матрицы. Пусть это столбец с индексом     

                             

 

5 шаг.    Этот шаг аналогичен первому.  Просматривая первого столбца матрицы

                                

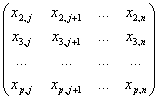
сверху вниз, найдем строку, начинающуюся с ненулевого элемента, затем найденную строку переставим с первой  строкой  этой матрицы.

Получим новую матрицу, которую обозначим также

                                   

в которой  .

6 шаг.  Этот шаг аналогичен второму. Разделим  первую строку  на   (умножим на  ). Получим: матрицу вида

                                   

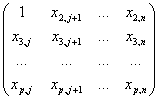
7 шаг.  Этот шаг аналогичен третьему шагу. Вычитая первую строку, умноженную на соответствующие коэффициенты, из последующих строк  матрицы, получим матрицу вида

                               

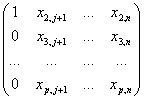
Продолжая процесс аналогичным образом,  придем к матрице верхнего треугольного вида.

Тензор

[править]

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Тензор (компания).

Те́нзор (от лат. tensus, «напряженный») — объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Частными случаями тензоров являются скаляры, векторы, билинейные формы и т.п. Термин «тензор» также часто служит сокращением для термина «тензорное поле», изучением которых занимаетсятензорное исчисление.

Тензор механического напряжения второго ранга. Компоненты тензора в трёхмерной декартовой системе координат образуют матрицу 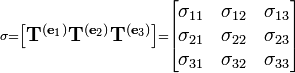 столбцами которой являются силы, действующие на  ,  , и   грани куба.

Часто тензор представляют как многомерную таблицу  , заполненную числами — компонентами тензора(где   — размерность векторного пространства, над которым задан тензор, а число сомножителей совпадает с т.н. валентностью или рангом тензора). Важно, что такое представление (кроме тензоров валентности ноль — скаляров) возможно только после выбора базиса (или системы координат): при смене базиса компоненты тензора меняются определённым образом.

Сам тензор как «геометрическая сущность» от выбора базиса не зависит, что можно наглядно видеть на примере вектора, являющегося частным видом тензора: компоненты вектора меняются при смене координатных осей, но сам вектор — образом которого может быть просто нарисованная стрелка — от этого не изменяется.