Действия над комплексными числами
Сравнение
означает,
что 
и 
(два
комплексных числа равны между собой
тогда и только тогда, когда равны их
действительные и мнимые части).
Сложение
Вычитание
Умножение
Деление
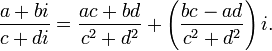
Геометрическая модель
Геометрическое представление комплексного числа
Рассмотрим
плоскость с прямоугольной
системой координат.
Каждому комплексному числу 
сопоставим
точку плоскости с координатами 
(а
также радиус-вектор,
соединяющий начало координат с этой
точкой). Такая плоскость называется комплексной.
Вещественные числа на ней занимают
горизонтальную ось, мнимая единица
изображается единицей на вертикальной
оси; по этой причине горизонтальная и
вертикальная оси называются
соответственно вещественной и мнимой осями.
Часто бывает удобно рассматривать на комплексной плоскости также полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и угол радиус-вектора точки (показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент). Подробнее см. ниже.
В этом наглядном представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него геометрически означает поворот радиус-вектора первого числа на угол, равный аргументу второго числа. Этот факт объясняет широкое использование комплексного представления в теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза».
Геометрическая модель комплексных чисел широко используется в планиметрии: многие планиметрические теоремы можно доказать как некоторые комплексные тождества. Часто этот метод даёт наиболее простое доказательство.
Связанные определения
Модуль, аргумент, вещественная и мнимая части
Пусть
—
комплексное число, где
и
— вещественные
числа.
Числа 
или 
и 
или 
называются
соответственно вещественной и мнимой (аналогично англ. real,
imaginary)
частями
.
Если
,
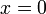то
называется мнимым или чисто
мнимым числом.Если
,
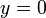то
является действительным
(вещественным) числом.
Модуль и аргумент
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль
комплексного числа
обозначается 
и
определяется выражением 
.
Часто обозначается буквами 
или 
.
Если
является вещественным
числом,
то
совпадает
с абсолютной
величиной этого
вещественного числа.
Для
любых 
имеют
место следующие свойства модуля. :
1) 
,
причём 
тогда
и только тогда, когда 
;;
2) 
(неравенство
треугольника);
3) 
;
4) 
.
Из
третьего свойства следует 
,
где 
.
Данное свойство модуля вместе с первыми
двумя свойствами вводят на множестве
комплексных чисел структуру
двумерного нормированного
пространства над
полем
.
5)
Для пары комплексных чисел 
и 
модуль
их разности 
равен
расстоянию между соответствующими
точками комплексной плоскости.
Угол 
(в
радианах) радиус-вектора точки,
соответствующей числу
,
называется аргументом числа
и
обозначается 
.
Из этого определения следует, что
; 
; 
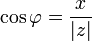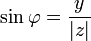.Для комплексного нуля значение аргумента не определено, для ненулевого числа аргумент определяется с точностью до
,
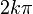где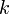 
—
любое целое число.Главным значением аргумента называется такое значение , что
.
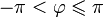Часто главное значение обозначается 
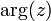[4].
Главное значение аргумента обратного
числа отличается знаком от аргумента
исходного: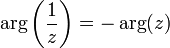 
.