[Править]Примеры
Рациональные числа, и только они, являются алгебраическими числами 1-й степени.
Мнимая единица i и
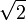являются
алгебраическими числами 2-й степени.
Сопряжёнными к ним являются соответственно
-i и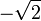 
.При любом натуральном числе n число
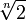является
алгебраическим степени n.
[Править]Свойства
Множество алгебраических чисел счётно, а следовательно, имеет меру нуль.
Множество алгебраических чисел плотно в комплексной плоскости.
Сумма, разность, произведение и частное двух алгебраических чисел (кроме деления на нуль) суть алгебраические числа, то есть множество всех алгебраических чисел образуетполе.
Корень многочлена с алгебраическими коэффициентами есть алгебраическое число, то есть поле алгебраических чисел алгебраически замкнуто.
Для всякого алгебраического числа существует такое натуральное
,
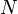что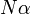 
— целое
алгебраическое число.Алгебраическое число степени имеет различных сопряжённых чисел (включая себя).
и
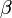сопряжены тогда
и только тогда,
когда существует автоморфизм поля
,
переводящий
в
.Любое алгебраическое число вычислимо, а следовательно, арифметично.
Порядок на множестве действительных алгебраических чисел изоморфен порядку на множестве рациональных чисел.
[Править]История
Впервые
алгебраические поля стал рассматривать Гаусс.
При обосновании теории биквадратичных вычетов он
развил арифметику целых гауссовых
чисел,
то есть чисел вида 
,
где
и 
— целые
числа.
Далее, изучая теорию кубических
вычетов, Якоби и Эйзенштейн создали
арифметику чисел вида 
,
где 
—
кубическийкорень
из единицы,
а
и
—
целые числа. В 1844 году Лиувилль доказал теорему о
невозможности слишком хорошего
приближения корней многочленов с
рациональными коэффициентами рациональными
дробями, и, как следствие, ввёл формальные
понятия алгебраических и трансцендентных
(то есть всех прочих вещественных) чисел.
Попытки доказать великую
теорему Ферма привели Куммера к
изучению полей
деления круга,
введению понятия идеала и
созданию элементов теории алгебраических
чисел. В работахДирихле, Кронекера, Гильберта и
других теория алгебраических чисел
получила свое дальнейшее развитие.
Большой вклад в неё внесли русские
математики Золотарев (теория
идеалов), Вороной (кубические
иррациональности, единицы кубических
полей), Марков (кубическое
поле), Сохоцкий (теория
идеалов) и другие.
Трисекция угла
[править]
Материал из Википедии — свободной энциклопедии
Трисекция угла — задача о делении заданного угла на три равные части построением циркулем и линейкой. Иначе говоря, необходимо построить трисектрисы угла — лучи, делящие угол на три равные части.
Наряду с задачами о квадратуре круга и удвоении куба является одной из классических неразрешимых задач на построение, известных со времён Древней Греции.
П. Л. Ванцель доказал в 1837 году, что задача разрешима только тогда, когда разрешимо в квадратных радикалах уравнение:
Например, трисекция осуществима для углов α = 360°/n при условии, что целое число n не делится на 3. Тем не менее, в прессе время от времени публикуются (неверные) способы осуществления трисекции угла циркулем и линейкой[1][2][3].