10.1 Комплексные числа

         В математике большую роль играют так называемые обратные операции, необходимость выполнения которых обычно приводит к расширению классов имеющихся объектов.

         Например, операция сложения. Когда-то люди не знали отрицательных чисел. Складывая положительные числа, в ответе всегда получались положительное число. Но обратная операция – вычитание – привела к необходимости рассматривать числа отрицательные.

         Операция умножения. Перемножая целые числа, в ответе всегда получаем также целые числа. Обратная операция – деление -приводит нас к необходимости рассматривать дробные, рациональные числа.

         Операция возведения в квадрат. Квадрат рационального числа есть всегда также число рациональное. Но обратная операция – извлечение квадратного корня – приводит к иррациональным числам ( , например, не является рациональным числом).

         Но та же самая операция извлечения квадратного корня дает и еще один класс чисел. Как известно, квадрат любого рационального числа есть число неотрицательное. Поэтому и квадратный корень можно извлечь только из неотрицательных чисел (например,  ). А как быть с  ? Чему он равен? Ведь нет такого рационального числа, квадрат которого был бы равен    – 9.

         Но, как говорится, если нельзя, но очень хочется, то можно. И желание извлекать корни из отрицательных чисел привело к новому классу чисел, называемых комплексными числами. Для их рассмотрения оказалось достаточным ввести всего лишь одно новое число

,

которое называется мнимой  единицей. Считается, что это «число» обладает всеми свойствами обычных чисел и имеет всего одно единственное новое свойство

,

так что, например,  . Числа, содержащие i, называются комплексными числами. Без них немыслима современная математика.

10.1.1 Алгебраическая форма комплексных чисел

         Пусть x и y – обычные числа. Число вида

z=x+iy

называется комплексным числом в алгебраической форме.

         x называют вещественной или действительной частью числа z и обозначают так:  ; y называют мнимой частью числа z и обозначают так:  . Число   называют комплексно сопряженным числу z. Действует следующее общее правило: «чтобы получить число, комплексно сопряженное данному, надо в нем заменить i на –i ».

         Рассмотрим операции над комплексными числами в алгебраической форме. Пусть даны два комплексных числа   и  .

         Равенство и сравнение комплексных чисел.

         Два комплексных числа считаются равными, если у них равны вещественные и мнимые части:

.

         Но вот операции типа «больше» и «меньше» для комплексных чисел не имеют смысла, то есть бессмысленно писать   или  . Совершенно непонятно, что больше   или  . Комплексные числа не упорядочены.

         Сложение и вычитание.

         Сложение и вычитание двух комплексных чисел определяются совершенно естественно

,

то есть надо сложить (или вычесть) отдельно вещественные и мнимые части чисел.

         Умножение.

Умножение двух комплексных чисел производится как умножение обычных чисел, надо лишь помнить, что  :

.

         Деление.

         Для деления комплексных чисел полезно запомнить следующее правило: чтобы разделить два комплексных числа друг на друга надо числитель и знаменатель умножить на число, комплексно сопряженное знаменателю. Тогда легко получить, что

.

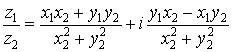         10.1.2 Геометрическая интерпретация комплексных чисел.

Рис. 10.1 Геометрическая интерпретация комплексного числа

         Пусть имеется комплексное число  . Возьмем на плоскости декартову систему координат и комплексному числу z поставим в соответствие точку на этой плоскости с координатами (x, y) (см. рис. 10.1). Таким образом, геометрически комплексные числа – это точки на плоскости (вспомните, что вещественные числа – это точки на числовой оси). Саму плоскость называют плоскостью комплексной переменной z.