Сопряжённые числа

Геометрическое представление сопряжённых чисел

Если комплексное число  , то число   называется сопряжённым (или комплексно сопряжённым) к   (обозначается также  ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.

Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.

•  (сопряжённое к сопряжённому есть исходное).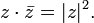

• 

• 

• 

• 

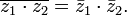
Обобщение:  , где   — произвольный многочлен с вещественными коэффициентами.

• 

• 

Значимость сопряжения объясняется тем, что оно является образующей группы Галуа  .

Представление комплексных чисел Алгебраическая форма

Запись комплексного числа   в виде  ,  , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что  ):

Тригонометрическая и показательная формы

Если вещественную   и мнимую   части комплексного числа выразить через модуль   и аргумент   ( ,  ), то всякое комплексное число  , кроме нуля, можно записать в тригонометрической форме

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:

где   — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

Формула Муавра и извлечение корней из комплексных чисел

Основная статья: Формула Муавра

Корни пятой степени из единицы(вершины пятиугольника)

Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

где   — модуль, а   — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.

Аналогичная формула применима также и при вычислении корней  -ой степени из ненулевого комплексного числа:

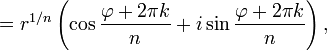
Отметим, что корни  -й степени из ненулевого комплексного числа всегда существуют, и их количество равно  . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного  -угольника, вписанного в окружность радиуса   с центром в начале координат (см. рисунок).

История

Впервые, по-видимому, мнимые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Кардано (1545), который счёл их непригодными к употреблению. Пользу мнимых величин, в частности, при решении кубического уравнения, в так называемом неприводимом случае (когда вещественные корни многочлена выражаются через кубические корни из мнимых величин), впервые оценил Бомбелли (1572). Он же дал некоторые простейшие правила действий с комплексными числами.

Выражения вида  , появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI—XVII веках, однако даже для многих крупных ученых XVII века алгебраическая и геометрическая сущность мнимых величин представлялась неясной. Лейбниц, например, писал: «Дух божий нашёл тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы».^[5]

Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным результатам, или, например, извлечение корня может привести к открытию какого-то нового типа чисел. Задача о выражении корней степени   из данного числа была решена в работах Муавра (1707) и Котса (1722).

Символ   предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова лат. imaginarius. Он же распространил все стандартные функции, включая логарифм, на комплексную область. Эйлер также высказал в 1751 году мысль об алгебраической замкнутости поля комплексных чисел. К такому же выводу пришел д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году.

Геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе Весселя (1799). Первые шаги в этом направлении были сделаны Валлисом(Англия) в 1685 году. Современное геометрическое представление, иногда называемое «диаграммой Аргана», вошло в обиход после опубликования в 1806-м и 1814-м годах работыЖ. Р. Аргана, повторявшей независимо выводы Весселя. Термины «модуль», «аргумент» и «сопряжённое число» ввёл Коши.

Арифметическая модель комплексных чисел как пар вещественных чисел была построена Гамильтоном (1837); это доказало непротиворечивость их свойств. Гамильтон предложил и обобщение комплексных чисел — кватернионы, алгебра которых некоммутативна.

  Построение поля комплексных чисел

Из курса школьной математики известно, что любое уравнение   имет решение при   . С другой стороны, квадратное уравнение не всегда имеет решение. Например, решения не имеет уравнение   . Возникает вопрос, нельзя ли сделать так, чтобы любое квадратное уравнение имело решение?

Предположим, что уравнение   имет решение. Число (абстрактный элемент, не принадлежащий полю вещественных чисел), которое является решением, обозначим буквой   , то есть   . Мы должны иметь возможность умножать это число на любое вещественное число. Значит, должны появиться числа вида   , где    -- вещественное число. Для них должна быть возможность сложения с любым вещественным числом. Поэтому должны появиться числа вида   .

        Определение 17.1   Числа вида   , где   и    -- вещественные числа, называются комплексными числами.         

Посмотрим, какие действия арифметики можно производить с комплексными числами. Сложение чисел должно удовлетворять обычным правилам, поэтому:

(17.1)

При вычислении произведения скобки раскроем привычным способом:

Так как   , то получим

(17.2)

Итак, результаты сложения и умножения комплексных чисел снова оказались комплексными числами. Операцию вычитания определить не сложно:

(17.3)

Рассмотрим операцию деления. Учтем, что при умножении числителя и знаменателя дроби на одно и то же число дробь не меняется:

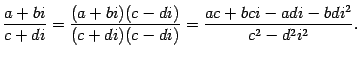
Так как   , то

(17.4)

Результат деления двух комплексных чисел оказывается снова комплексным числом. Как видно из полученной формулы, деление нельзя выполнить лишь в том случае, когда   , но в этом случае делитель   тоже равен нулю. Следовательно, невозможно лишь деление на нуль, что соответствует обычным правилам действий с числами.

Итак, мы вроде бы расширили множество вещественных чисел. Но есть в этом построении один существенный пробел. Мы предположили, что есть такое число   , что   . А, может быть, его на самом деле нет?² Чтобы исправить это упущение, используем для построения комплексных чисел уже существующее множество.

Пусть    -- множество пар вещественных чисел:   . На этом множестве определим операции

1. сложения:

2. вычитания:

3. умножения:

4. деления:

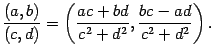
Очевидно, что комплексное число, как оно было определено раньше, -- просто другая форма записи пары вещественных чисел   , где вместо запятой стоит "+", а второй элемент пары выделяется умножением на букву   . В новой форме записи вещественные числа -- это пары   , числу   соответствует пара   , сложение, вычитание, умножение и деление пар чисел и комплексных чисел происходят по одинаковым правилам. Таким образом, комплексные числа стали реально существующим множеством.

Однако в математике, в силу традиции, используется запись комплексного числа   , введенная в начале раздела³. Причем принято считать, что

Можно проверить, что комплексные числа образуют поле. В нем обратным элементом к комплексному числу   служит результат деления 1 на   :

Это поле называется полем комплексных чисел и обозначается   .

Число   называется мнимой единицей, числа    -- мнимыми числами. Если   , то число   называется вещественной частью комплексного числа и обозначается   , число  называется мнимой частью и обозначается   . Число   называется сопряженным числу   и обозначается   , то есть   .

        Замечание 17.1   В электротехнике, где буква   обозначает ток, мнимую единицу обозначают буквой   .         

Если операции сложения, вычитания и умножения комплексных чисел соответствуют обычным правилам раскрытия скобок, то для выполнения деления нужно или запомнить формулу (17.4), или, что проще, каждый раз при выполнении деления умножать числитель и знаменатель дроби на число, сопряженное знаменателю.

        Пример 17.1   Пусть   ,   . Тогда:

Вычислим еще   :