2. Критерий интегрируемости функций. Классы интегрируемых функций. Свойства интеграла, связанные с операциями над функциями.

Критерий Лебега: f(x) интегрируема на [a;b] тогда, когда множество Е-точек разрыва f на [a;b] можно покрыть конечным числом интервалов сколь угодно малой суммарной длины.

Классы интегрируемых функций:

Т1. Если f непрерывна на [a;b], то она интегрируема на нем. Следствие: Всякая элементарная функция непрерывна на 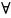отрезке целиком лежащим в ее области определения.

Т2. (смотри критерий Лебега). Функция f(x) ограничена на [a;b] и имеет на нем конечное число точек I рода и интегрируема на нем.

Т3. Монотонная на [a;b] функция интегрируема на нем. Определение: f(x) является кусочно-непрерывной (кусочно-монотонной) на [a;b] если этот отрезок можно разбить на конечное число отрезков, на каждом из которых функция непрерывна (монотонна). Следствие: кусочно-непрерывная (монотонная) на отрезке [a;b] интегрируема на нем.

Свойства определенного интеграла. Замечание: если f(x) интегрируема на [a;b], то число не зависящее от того, какой буквой обозначается переменная интегрирования = .

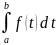Основные свойства определенного интеграла (6 свойств):

1. Принять, что

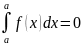
2. При b>a выполняется

3. Пусть функции f(x) и g(x) интегрируемы на сегменте [a, b]. Тогда функции f(x)±g(x), f(x)·g(x), так же интегрируемы на [a, b]. При этом для алгебраической суммы справедливо равенство:

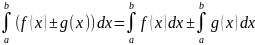
4. Пусть функция f(x) интегрируема на [a, b]. Тогда и функция C·f(x) (где С - постоянная) интегрируема на [a, b]. Тогда

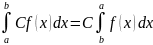
5. Пусть функция f(x) интегрируема на [a, b]. Тогда эта функция интегрируема на любом сегменте [c, d], содержащемся в [a, b].

6. Пусть функция f(x) интегрируема на сегменте [a, c] и [c, b]. Тогда она интегрируема на сегменте [a, b]. При этом справедливо равенство: .

3. Свойства интеграла, связанные с отрезками интегрирования и неравенствами. Оценки интегралов.

Свойства, связанные с отрезками интегрирования

1. Если f(x)интегрируемы на [a, b], то она интегрируема на любом отрезке [c, d] на [a, b].

2. Свойство адитивности по отрезку: если f(x) интегрируема на [a, b] и c - точка интервала (a; b), когда f(x) интегрируема на [a, c] и [c, b] ; (*).

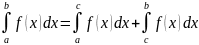Верно и обратное утверждение: если f(x) интегрируема на отрезке [a, c] и [c, b], то она интегрируема на [a, b] и справедливо (*).

Расширение понятия определенного интеграла: 1) если b=a, то по определению 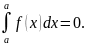2) если b a, то по определению при b<a.

3. Если f(x) интегрируема на отрезке [a, b], то для любых точек C1, C2, C3, лежащих в [a, b] справедливо равенство: .

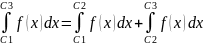Доказательство: по свойству 1 и расширенному определению интеграла, все 3 интеграла существуют в этом пространстве: а) C1< C2<C3. Свойство 3 вытекает из свойства 2, т.е. [C1, C3] разбивается на [C1, C2] и [C2, C3]. б) C1< C3<C2. По свойству 2 отрезок [C1, C2] разбивается на [C1, C3] и [C3, C2] ⇒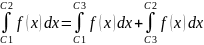 = - 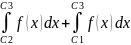. в) C1=C2<C3. Тогда , где 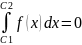- по расширенному определению.

Свойства, связанные с неравенствами

1.Если f(x) интегрируема на [a, b] и f(x)≥0, x [a, b], то

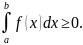
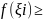Доказательство: Т (f, ξ)= , где и ( =xi-xi-1). Так как f(x) интегрируема на [a, b], то d(Т)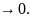 По теореме о пределе 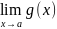≥0 (g(x)≥0) ⇒ = ≥0, то и требовалось доказать.

Следствие: если f(x) и g(x) интегрируемы на [a, b] и f(x) ≥ g(x) x [a, b], то .

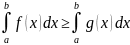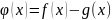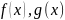Определение: рассмотрим функцию , x [a, b]. 1) интегрируема на [a, b] по свойству линейности (т.к. интегрируемы). 2) по условию следствия x [a, b], тогда ≥0 x [a, b]. Применим предыдущее свойство к ⇒ 0, - , = ≥ .

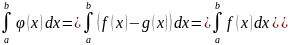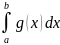2.Пусть выполняются следующие условия: 1) f(x) интегрируема на [a, b]. 2) f(x) ≥0 x [a, b]. 3) Существует x0 лежащее в [a, b] такое, что f(x0)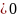 . 4) f(x) непрерывна в точке x0⇒ .

3. Если f(x) интегрируема на [a, b], то 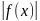интегрируема на [a, b] и справедливо неравенство 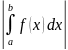не превосходит dx. В обратную сторону утверждение неверно.

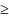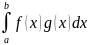4.Пусть f(x) и g(x) интегрируемы на [a, b], g(x) 0 на [a, b]. Пусть m=inf f(x) на [a, b], М=sup f(x)на [a, b], тогда справедливо неравенство: m ≤ ≤M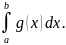

Доказательство: по определению точной верхней и нижней грани m≤f(x)≤M x [a, b], умножим неравенство на g(x) 0⇒ mg(x)≤f(x)g(x)≤Mg(x) – интегрируемы на [a, b] ⇒ по следствию свойства 1 ≤ ≤

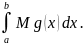
Три оценки определенных интегралов.

1^я. Пусть функция f(x) интегрируема и неотрицательна на сегменте [a, b], т.е. f(x)≥0 при x [a, b].

Тогда

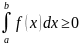
2^я. Пусть функции f(x) и g(x) интегрируемы на [a, b] и пусть на [a, b]выполняется неравенство: f(x)≥g(x).

Тогда справедливо неравенство:

3^я. Пусть функции f(x) и g(x) интегрируемы на [a, b] и пусть на [a, b]выполняется неравенство: g(x)≥0. Пусть кроме того числа m, M – точные нижние и верхние грани f(x) на [a, b]. Тогда справедливы следующие неравенства:

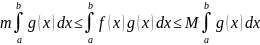
Доказательство: В соответствии с определением m и M должно выполняться: m≤f(x)≤M на [a, b]. Умножим эти неравенства на g(x).

m g(x)≤f(x) g(x)≤M g(x) --->