
- •Ахметова Наиля Абдулхамитовна
- •Введение
- •1. Элементы комбинаторики
- •1.1. Перестановки. Размещения. Сочетания
- •Теорема.
- •1.2. Задачи по комбинаторике
- •2. Функции алгебры логики
- •2.1. Элементарные функции алгебры логики
- •Пример 2.
- •2.2. Формульное задание функций алгебры логики
- •Упрощение записи формул:
- •Теорема о замене подформул на эквивалентные
- •Некоторые свойства элементарных функций
- •Следствия из свойств элементарных функций
- •Пример 3:
- •2.3 Принцип двойственности
- •Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
- •Пример 3. Покажем, что функция х1х2 двойственна к x1&x2, функция х1х2 двойственна к функции x1|x2.
- •Принцип двойственности
- •Лемма о несамодвойственной функции
- •2.4 Разложение булевой функции по переменным
- •Теорема о разложении функции по переменным
- •2.5. Полнота, примеры полных систем
- •Полные системы
- •Представление функции в виде полинома Жегалкина
- •Теорема Жегалкина
- •2.6. Замыкание и замкнутые классы
- •Важнейшие замкнутые классы в р2
- •Теорема Поста о полноте
- •Примеры использования теоремы Поста.
- •3. Составим критериальную таблицу для другой полной системы функций из р2: {0, 1,x1x2,x1x2}.
- •Теорема о достаточности четырех функций.
- •2.7. Функции k - значной логики
- •Теорема о полной в Рk системе функций
- •2.8. Задачи и упражнения по функциям алгебры логики
- •1. Построить таблицы соответствующих функций, выяснить, эквивалентны ли формулы и :
- •2. Построив таблицу для соответствующих функций, убедитесь в справедливости следующих эквивалентностей:
- •3. Минимизация булевых функций
- •3.1. Минимизация нормальных форм
- •Алгоритм Квайна построения сокращенной днф.
- •Метод Блейка
- •Алгоритм построения сокращенной днф с помощью кнф (метод Нельсона)
- •Построение всех тупиковых днф.
- •Алгоритм минимизации функций в классе днф
- •Алгоритм минимизации функций в классе кнф
- •Алгоритм минимизации функций в классе нормальных форм
- •3.2 Минимизация частично определенных функций
- •Алгоритм минимизации частично определенных функций в классе днф
- •Алгоритм минимизации частично определенных функций в классе кнф
- •Метод минимизирующих карт Карно
- •3.3 Задачи по минимизации и доопределению булевых функций
- •4. Логика высказываний
- •4.1. Введение в логику высказываний
- •4.2. Задачи по алгебре высказываний
- •Список литературы
3.3 Задачи по минимизации и доопределению булевых функций
1. Из заданного множестваАэлементарных конъюнкций выделить простые импликанты функцииf:
1) A
=
![]() ,
,![]() =
(00101111);
=
(00101111);
2) A
=
![]() ,
,![]() =
(01111110);
=
(01111110);
3) A
=
![]() ,
,![]() =
(1010111001011110);
=
(1010111001011110);
4) A
=
![]() ,
,![]() =
(1011);
=
(1011);
5) A
=
![]() ,
,![]() =
(00111011);
=
(00111011);
6) A
=
![]() ,
,![]() =
(00101111).
=
(00101111).
2. По заданной ДНФ с помощью метода Блейка построить сокращенную ДНФ:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
3.Построить сокращенную ДНФ по заданной КНФ:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
4. Изобразив
множествоNfфункции![]() вEn,
найдйте коды максимальных интервалов
и построитьйте сокращенную ДНФ:
вEn,
найдйте коды максимальных интервалов
и построитьйте сокращенную ДНФ:
1)
![]() =
(11110100); 2)
=
(11110100); 2)![]() = (01010011);
= (01010011);
3)
![]() =
(11010011); 4)
=
(11010011); 4)![]() = (11100111);
= (11100111);
5)
![]() =
(1111100001001100); 6)
=
(1111100001001100); 6)![]() =
(0001011111101111);
=
(0001011111101111);
7)
![]() =
(1110011000000111); 8)
=
(1110011000000111); 8)![]() =
(1111111111111000).
=
(1111111111111000).
5.С помощью алгоритма Квайна построить сокращенную ДНФ для функцииf, заданной вектором своих значений:
1)
![]() =
(01110110); 2)
=
(01110110); 2)
![]() =
(10111101);
=
(10111101);
3)
![]() =
(00101111); 4)
=
(00101111); 4)![]() =
(11100100);
=
(11100100);
5)
![]() =
(0001101111011011); 6)
=
(0001101111011011); 6)![]() =
(0000111111110110);
=
(0000111111110110);
7)
![]() =
(1111111101111110); 8)
=
(1111111101111110); 8)![]() =
(0000111101111111).
=
(0000111101111111).
6.Найти сокращенную ДНФ функцииfс помощью минимизирующей карты:
1)
![]() =
(01010111); 2)
=
(01010111); 2)![]() =
(11011011);
=
(11011011);
3)
![]() =
(10110000); 4)
=
(10110000); 4)![]() =
(11101111);
=
(11101111);
5)
![]() =
(0001101111011111); 6)
=
(0001101111011111); 6)![]() =
(0011110111111101);
=
(0011110111111101);
7)
![]() =
(0011110111011110); 8)
=
(0011110111011110); 8)![]() =
(0010101111011111).
=
(0010101111011111).
7.С помощью минимизирующих карт построить сокращенную ДНФ для частично определенной функцииf, заданной векторно (прочерки соответсвуют неопределенным значениям):
1)
![]() =
(01--01-1);
=
(01--01-1);
2)
![]() =
(1-01--10);
=
(1-01--10);
3)
![]() =
(1---0-10);
=
(1---0-10);
4)
![]() =
(0--10-1-);
=
(0--10-1-);
5)
![]() =
(10-1-011-0--1-01);
=
(10-1-011-0--1-01);
6)
![]() =
(0--1---0--1-1-01);
=
(0--1---0--1-1-01);
7)
![]() =
(--01-1-00----1-0);
=
(--01-1-00----1-0);
8)
![]() =
(-10-1-11-01-0---).
=
(-10-1-11-01-0---).
8.Найти длину сокращенной ДНФ функцииf:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
9)
![]()
9.Выяснить, является ли ДНФDа) тупиковой, б) кратчайшей, в)минимальной:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
10.Применить алгоритм упрощения к ДНФ:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
11.По заданной сокращенной ДНФDпостроить минимальные ДНФ:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
7)
![]()
8)
![]()
12.С помощью таблицы Квайна построить все тупиковые ДНФ функцииf, заданной вектором своих значений:
1) ![]() =
(01111100); 2)
=
(01111100); 2) ![]() =
(01111110);
=
(01111110);
3) ![]() =
(00011111); 4)
=
(00011111); 4) ![]() =
(1111100001001100);
=
(1111100001001100);
5) ![]() =
(1110100001101000); 6)
=
(1110100001101000); 6) ![]() =
(1110011000010101);
=
(1110011000010101);
7) ![]() =
(0001011110101110); 8)
=
(0001011110101110); 8) ![]() =
(0001101111100111).
=
(0001101111100111).
4. Логика высказываний
4.1. Введение в логику высказываний
Определение.Высказыванием называется повествовательное предложение, о котором имеет смысл говорить, что оно истинно или ложно.
Примеры высказываний: «2х2=4», «Волга впадает в Черное море», «Москва – столица России». Первое и третье высказывания истинны, второе – ложно. Предложение «х +y = 4» не является высказыванием, т.к. оно может быть истинным при некоторых значенияххиyи ложным при других значениях. Из простых, атомарных высказываний можно сооружать сложные высказывания. Например, из двух высказываний: «Москва стоит на берегу Невы» и «Санкт-Петербург стоит на берегу Невы», из которых первое ложно, второе истинно, можно соорудить более сложные высказывания: «Москва стоит на берегу Невы или Санкт-Петербург стоит на берегу Невы» (истинное) или «Москва стоит на берегу Невы и Санкт-Петербург стоит на берегу Невы» (ложное).
В логике высказываний простые высказывания являются булевыми переменными, принимающими значения «истина» (и) или «ложь» (л). Переменной (и) соответствует 1, переменной (л) – 0. Для них стандартным образом определяются булевы функции: дизъюнкция высказываний, конъюнкция (два последних примера), отрицание, эквивалентность, сумма по mod2 (исключающее «или»), импликация.
Рассмотрим более подробно последнюю
функцию
![]() ,
гдеPиQ– высказывания, т.е. утверждение типа:
«
,
гдеPиQ– высказывания, т.е. утверждение типа:
«![]() влечет
влечет![]() »
или «из
»
или «из![]() следует
следует![]() »,
например, «Если 2х2=5, то Москва – столица».
Не математик найдет это выражение
ложным, ибо ему кажется, что в выражении
«
»,
например, «Если 2х2=5, то Москва – столица».
Не математик найдет это выражение
ложным, ибо ему кажется, что в выражении
«![]() влечет
влечет![]() »
»![]() должно по смыслу вытекать из
должно по смыслу вытекать из![]() ,
только в этом случае утверждение истинно.
Но тогда получается, что логическая
связка «
,
только в этом случае утверждение истинно.
Но тогда получается, что логическая
связка «![]() »
зависит от смысла высказываний. Математики
импликацию определяют стандартной
таблицей истинности, которая не
противоречит «здравому смыслу»: «л
»
зависит от смысла высказываний. Математики
импликацию определяют стандартной
таблицей истинности, которая не
противоречит «здравому смыслу»: «л![]() л»
и «л
л»
и «л![]() и»
– эти утверждения истинны, так как из
ложной посылки можно получить как
ложное, так и истинное утверждение.
«и
и»
– эти утверждения истинны, так как из
ложной посылки можно получить как
ложное, так и истинное утверждение.
«и![]() и»
– истинное утверждение, так как из
верной посылки с помощью верных
рассуждений можно получить только
истинное утверждение. «и
и»
– истинное утверждение, так как из
верной посылки с помощью верных
рассуждений можно получить только
истинное утверждение. «и![]() л»
– ложное утверждение, ибо из истинного
утверждения с помощью верных рассуждений
мы не сможем прийти к ложному результату.
л»
– ложное утверждение, ибо из истинного
утверждения с помощью верных рассуждений
мы не сможем прийти к ложному результату.
Простые высказывания (булевы переменные)
будем обозначать буквами
![]() ,
если понадобится, с индексами. Булевы
функции от этих высказываний –
,
если понадобится, с индексами. Булевы
функции от этих высказываний –![]() .
В логике высказываний можно ввести
стандартное для функций алгебры логики
понятие формулы. Формулы будем обозначать
буквами латинского алфавита
.
В логике высказываний можно ввести
стандартное для функций алгебры логики
понятие формулы. Формулы будем обозначать
буквами латинского алфавита![]() где в скобках перечислены входящие в
формулу булевы переменные.
где в скобках перечислены входящие в
формулу булевы переменные.
Формула
![]() называетсятавтологией, если
она принимает значение 1 для любого
набора значений входящих в нее переменных,
т.е. если она реализует функцию константа
1.
называетсятавтологией, если
она принимает значение 1 для любого
набора значений входящих в нее переменных,
т.е. если она реализует функцию константа
1.
Формула
![]() называетсяпротиворечием, если
она принимает значение 0 на всех наборах
значений переменных
называетсяпротиворечием, если
она принимает значение 0 на всех наборах
значений переменных![]() (реализует функцию константа 0).
(реализует функцию константа 0).
Формула
![]() называетсяопровержимой,если существует набор
называетсяопровержимой,если существует набор![]() значений
значений![]() ,
такой что
,
такой что![]()
Формула
![]() называетсявыполнимой, если
существует набор
называетсявыполнимой, если
существует набор![]() значений
значений![]() ,
такой что
,
такой что![]()
С точки зрения логики тавтология – логический закон, так как при любой подстановке вместо переменных конкретных высказываний мы получаем истинное высказывание. Перечислим наиболее важные тавтологии (А,В,С– произвольные формулы):
 т.е.
т.е. Эта тавтология называетсязаконом
исключенного третьего или tertium
nondatur.
Эта тавтология называетсязаконом
исключенного третьего или tertium
nondatur.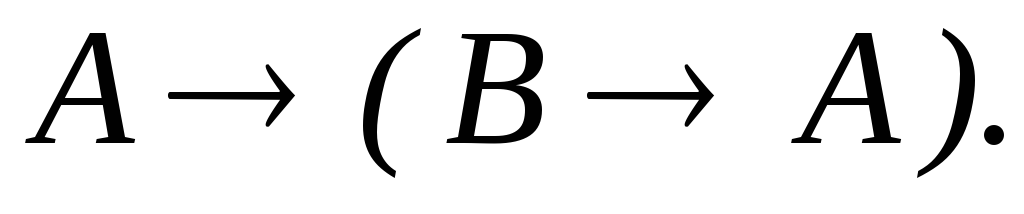
 –цепное рассуждение.
–цепное рассуждение.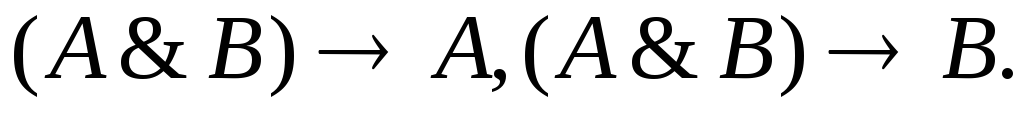
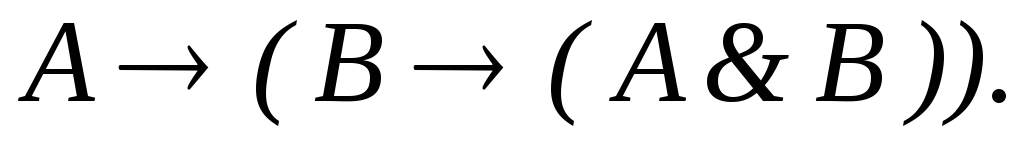


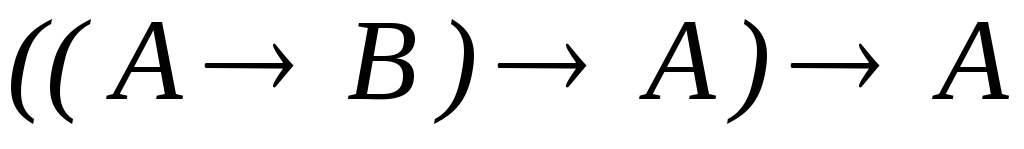 –закон Пирса.
–закон Пирса.
Любую из этих тавтологий можно обосновать, составив таблицу истинности и показав, что соответствующая функция есть константа. К этому же результату можно прийти с помощью эквивалентных преобразований.
Докажем, что
![]() – тавтология.
– тавтология.
![]()
При доказательстве различных утверждений мы пользуемся «рассуждениями».
Рассуждениеназывается правильным,
если из конъюнкции посылок![]() следует заключениеD,
это записывается:
следует заключениеD,
это записывается:![]() ,
т.е. всякий раз, когда все посылки истинны,
то заключение тоже истинно. Таким
образом, чтобы установить правильность
рассуждений, надо показать, что формула
,
т.е. всякий раз, когда все посылки истинны,
то заключение тоже истинно. Таким
образом, чтобы установить правильность
рассуждений, надо показать, что формула![]() является тавтологией. Действительно,
если какая-то из посылок ложна, то
является тавтологией. Действительно,
если какая-то из посылок ложна, то![]() и импликация принимает значение 1. Если
все посылки истинны и рассуждения верны,
то заключение тоже должно быть верно и
импликация вновь принимает значение
1.
и импликация принимает значение 1. Если
все посылки истинны и рассуждения верны,
то заключение тоже должно быть верно и
импликация вновь принимает значение
1.
Пример 1.Рассмотрим следующее
«рассуждение»: «Если число 5 – простое,
то оно нечетное. Число 5 – нечетное,
следовательно, оно простое». Число 5
действительно простое, но сами рассуждения
неверны. Введем обозначения для
высказываний:х– «5 – число простое»,y– «5 – число нечетное».
Тогда посылками будут![]() заключением будет х. Рассуждения шли
по схеме
заключением будет х. Рассуждения шли
по схеме![]() Строим формулу для определения
правильности рассуждения:
Строим формулу для определения
правильности рассуждения:![]() Проверим,
Проверим,
![]()
На наборе х = 0,y= 1 формула принимает значение 0, следовательно, она не является тавтологией. Эта формула будет тавтологией, еслих=y, т.е. простое число и нечетное число – эквивалентные понятия. «Здравый смысл подсказывает», что в этом случае, действительно, рассуждения верны.
Пример 2.Если Петр занимается спортом, то Петр никогда не болеет. Петр занимается спортом, следовательно, он не болеет.
Введем обозначения для высказываний: x– «Петр занимается спортом»,y– «Петр не болеет».
Схема
рассуждений
![]() Проверим правильность этой схемы
рассуждений:
Проверим правильность этой схемы
рассуждений:![]()
Распространенные схемы правильных
рассуждений:![]() и
и![]() .
Правильность первой схемы доказана в
примере 2. Докажем правильность второй
схемы:
.
Правильность первой схемы доказана в
примере 2. Докажем правильность второй
схемы:
![]()
Рассмотрим высказывание вида
![]() гдеА – конъюнкция посылок,В–
заключение. Если формулаА –
тавтология и рассуждения логически
правильны, то заключениеВпринимает
значение «истина», что следует из таблицы
истинности для импликации. Такиеметоды
доказательстваистинности заключения
называютсяпрямыми. Иногда
удобнее доказать истинность другого
высказывания, эквивалентного данному.
Такие формы доказательства называютсякосвенными. Одним из них
является методдоказательства от
противного.
гдеА – конъюнкция посылок,В–
заключение. Если формулаА –
тавтология и рассуждения логически
правильны, то заключениеВпринимает
значение «истина», что следует из таблицы
истинности для импликации. Такиеметоды
доказательстваистинности заключения
называютсяпрямыми. Иногда
удобнее доказать истинность другого
высказывания, эквивалентного данному.
Такие формы доказательства называютсякосвенными. Одним из них
является методдоказательства от
противного.
1. Предполагаем, что высказывание
![]() ложно и приходим к противоречию, получаем,
что истинными являются два высказывания:
ложно и приходим к противоречию, получаем,
что истинными являются два высказывания:![]() и
и![]() ,
т.е.
,
т.е.![]() Применимость этой формы доказательства
оправдывается следующей эквивалентностью:
Применимость этой формы доказательства
оправдывается следующей эквивалентностью:![]()
2. Существуют и другие схемы доказательства
от противного. Предполагаем, что из
![]() следует
следует![]() и приходим к тому, что истинными
оказываются
и приходим к тому, что истинными
оказываются![]() и
и![]() или
или![]() и
и![]() .
Эти схемы основаны на эквивалентности
.
Эти схемы основаны на эквивалентности![]() или
или![]() .
.
Действительно,
![]() и
и![]()
Другой метод косвенного доказательства
– доказательство по закону
контрапозиции, когда
вместо истинности![]() мы доказываем истинность
мы доказываем истинность![]() .
Действительно,
.
Действительно,![]()
Рассмотрим на конкретных задачах применение исчисления высказываний.
Пример 3.Записать составное высказывание в виде формулы, употребляя булевы переменные для обозначения простых высказываний.
а) если идет дождь, то дует ветер и становится холодно;
б) если дует ветер, идет дождь;
в) ветер дует тогда и только тогда, когда идет дождь;
г) неверно, что ветер дует тогда и только тогда, когда нет дождя.
Решение. Введем обозначения:х– «идет дождь»,у– «дует ветер»,z–«становится холодно».
Тогда
приведенные высказывания можно записать
в виде следующих формул: а)
![]() б)
б)![]() в)
в)![]() г)
г)![]() .
.
Пример 4. Выяснить, являются ли следующие рассуждения логически верными.
Если Джонс не встречал ночью Смита, то Смит был убийцей или Джонс лжет. Если Смит не был убийцей, то Джонс не встречал Смита этой ночью, и убийство имело место после полуночи. Если убийство имело место после полуночи, то Смит был убийцей или Джонс не лжет. Следовательно, Смит был убийцей.
Решение. Введем логические
переменные:х– «Джонс не встречал
ночью Смита»,у– «Смит убийца»,z– «Джонс лжет»,t–
«убийство состоялось после полуночи».
Прежде чем записать формулу, надо
уточнить по условию задачи в каком
контексте употребляется союз «или».
Когда мы говорим «А или В», мы можем
подразумевать две разные ситуации: а)![]() или б)
или б)![]() Во втором случае высказыванияАиВне могут быть одновременно
истинными. Чтобы подчеркнуть этот
момент, обычно говорят «либоА, либоВ». В нашей задаче нет такой оговорки,
поэтому мы можем для записи высказывания:
«Смит был убийцей или Джонс не лжет»
использовать формулу
Во втором случае высказыванияАиВне могут быть одновременно
истинными. Чтобы подчеркнуть этот
момент, обычно говорят «либоА, либоВ». В нашей задаче нет такой оговорки,
поэтому мы можем для записи высказывания:
«Смит был убийцей или Джонс не лжет»
использовать формулу![]() .
Итак, мы имеем посылки:
.
Итак, мы имеем посылки:![]() ,
,![]() ,
,![]() заключение:у. Надо составить формулу:
заключение:у. Надо составить формулу:
![]() и посмотреть, будет ли она тавтологией:
и посмотреть, будет ли она тавтологией:
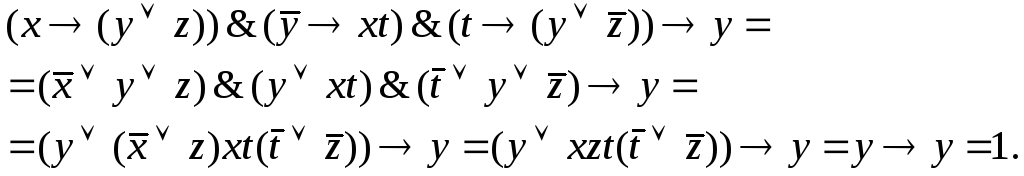
Следовательно, рассуждения логически правильны.
Пример 5.Проверить совместность утверждений.
Либо свидетель не был запуган, либо, если Генри покончил жизнь самоубийством, то записка была найдена. Если свидетель был запуган, то Генри не покончил жизнь самоубийством. Если записка была найдена, то Генри покончил жизнь самоубийством.
Решение.Введем булевы переменные: х – «свидетель не запуган», у – «Генри покончил самоубийством»,z– «записка найдена». Составим конъюнкцию посылок и посмотрим, не является ли она противоречием.
Здесь употреблено выражение «либо...,
либо...», поэтому первое составное
высказывание следует записать в виде
![]() что эквивалентно
что эквивалентно![]() Конъюнкция посылок имеет вид:
Конъюнкция посылок имеет вид:
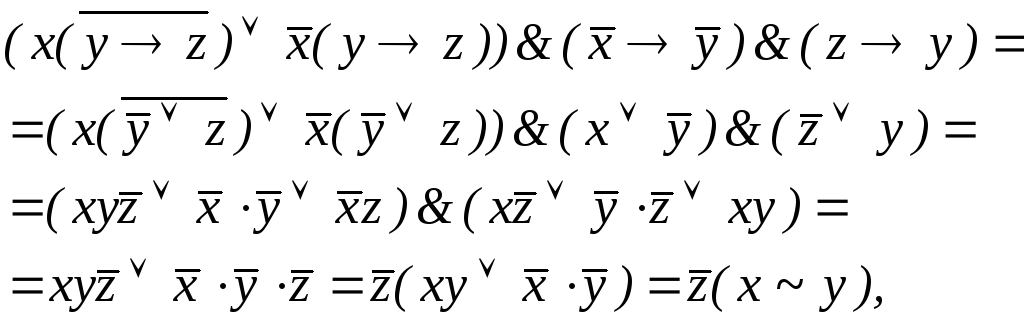
это не равно тождественному 0, следовательно, высказывания не являются противоречивыми.
Пример 6.Четыре ученицы: Маша (М), Нина (Н), Ольга (О) и Поля (П) участвовали в соревнованиях и заняли первые 4 места. На вопрос, кто какое место занял, было дано 3 ответа:
О – второе, П – третье;
О – первое, Н – второе;
М – второе, П – четвертое.
В каждом из этих ответов одна часть верна, а другая нет. Какое место заняла каждая девушка?
Решение.Введем булевы переменные:х– «О – второе»,у– «П –
третье»,z– «О –
первое»,t– «Н –
второе»,u– «М –
второе»,– «П
– четвертое». Получим систему уравнений:![]() так как еслиxистинно,
тогдаyложно, а
так как еслиxистинно,
тогдаyложно, а![]() – истинно и
– истинно и![]() либо
либо![]() Аналогично,
Аналогично,![]() Удобнее записать эту систему следующим
образом:
Удобнее записать эту систему следующим
образом:![]()
Отсюда
![]() или
или![]() окончательно,
окончательно,![]()
Кроме
того,
![]() так как одна ученица не может занять 2
места и одно место не может быть занято
двумя ученицами. В результате в последнем
уравнении останется единственный
ненулевой член
так как одна ученица не может занять 2
места и одно место не может быть занято
двумя ученицами. В результате в последнем
уравнении останется единственный
ненулевой член![]() Отсюда
Отсюда![]() или О – первая, М – вторая, П – третья,
Н – четвертая.
или О – первая, М – вторая, П – третья,
Н – четвертая.
Пример 7. Во время перемены в классе были Аня, Борис, Ваня и Майя. Один из них разбил окно. На вопрос:”Кто разбил окно?”, были даны ответы:
Аня: 1) Я не разбивала. 2) Я сидела и читала. 3) Майя знает, кто разбил.
Борис: 1) Я этого не делал. 2) С Майей я давно не разговариваю. 3) Это сделал Ваня.
Ваня: 1) Я не виновен. 2) Разбила Майя. 3) Борис лжёт, говоря, что разбил я.
Майя: 1) Я не разбивала. 2) Это вина Ани. 3) Борис знает, что я не виновна, т.е. мы с ним беседовали во время перемены.
Затем каждый признался, что из трёх ответов каждого, два – истинны, а один ложный. Кто разбил окно?
Решение.Введем булевы
переменные. Высказывания, принадлежащие
Ане, обозначим буквами![]() с индексами
с индексами![]() ;
высказывания, принадлежащие Борису –
;
высказывания, принадлежащие Борису –![]() соответственно, принадлежащие Ване –
соответственно, принадлежащие Ване –![]() и принадлежащие Майе –
и принадлежащие Майе –![]() .
.
Запишем все формулы, которые являются тавтологиями, получим уравнения:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Выпишем все противоречия:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Чтобы иметь возможность воспользоваться этими противоречиями, возьмём конъюнкцию двух тавтологий:
![]() и
и![]()
что тоже
будет тавтологией. Получим
![]()
В![]() этой формуле слева останется всего три
ненулевых члена:
этой формуле слева останется всего три
ненулевых члена:
![]() или
или![]() Последнее уравнение даёт
Последнее уравнение даёт![]()
![]() Так как
Так как![]() и
и![]() то
то![]() и следовательно,
и следовательно,![]() а
а![]() Следовательно, окно разбила Аня.
Следовательно, окно разбила Аня.
Рассмотрим еще одну задачу, для решения которой не требуется аппарат логики высказываний, но тем не менее эта задача относится к логическим задачам.
Пример 8. В кафе встретились три друга: скульптор Белов, скрипач Чернов и художник Рыжов. «Замечательно, что один из нас имеет белые, один черные, а один рыжие волосы, но ни у кого цвет волос не совпадает с фамилией», – заметил черноволосый. «Ты прав», – сказал Белов. Какой цвет волос у художника?
Решение. Составим таблицу.
|
Фамилия Цвет волос |
Б |
Ч |
Р |
|
б |
0 |
|
|
|
ч |
|
0 |
|
|
р |
|
|
0 |
Н
Фамилия Цвет
волос Б Ч Р б 0 1 0 ч 0 0 1 р 1 0 0
![]()
|
Фамилия Цвет волос |
Б |
Ч |
Р |
|
б |
0 |
0 |
1 |
|
ч |
1 |
0 |
0 |
|
р |
0 |
1 |
0 |
Из условия задачи ясно, что черноволосый не Белов, поэтому первый вариант не подходит. Следовательно, Белов – рыжий, Чернов – белый, Рыжов – черный.
Пример 9.На склад, имеющий два помещения для хранения больших количеств двух видов топлива – угля и кокса, каждого отдельно, поступают грузовики, каждый всякий раз с одним из этих видов топлива. К механизму, открывающему шахты, предъявляется требование, чтобы он открыл шахту в помещении для угля, если прибывает грузовик с этим топливом, и шахту в помещении для кокса, если прибывает грузовик с коксом. Для обеспечения хорошей сортировки топлива было предъявлено дополнительное требование: всякий раз в помещение склада впускается только один грузовик и открывается лишь одна шахта.
Спрашивается, имеет ли этот механизм также следующее свойство: если не въехал в помещение склада грузовик с углем, то шахта для угля не откроется, а если не въехал грузовик с коксом, то не откроется шахта для кокса.
Решение.Введем булевы переменные: высказывание
« прибыл грузовик с углем» обозначим
черезx, « прибыл
грузовик с коксом» –y,
«открыта шахта для угля» –z,
«открыта шахта для кокса» –t.
Тогда посылками будут:
![]()
![]() заключение
заключение![]() Задача сводится к тому, чтобы выяснить,
правильны ли рассуждения
Задача сводится к тому, чтобы выяснить,
правильны ли рассуждения![]() ,
т. е. вытекает ли это заключение из
конъюнкции посылок. Кроме того, имеются
два дополнительных условия, что может
въехать только одна машина и открывается
лишь одна дверь. Эти условия можно задать
равенствами:
,
т. е. вытекает ли это заключение из
конъюнкции посылок. Кроме того, имеются
два дополнительных условия, что может
въехать только одна машина и открывается
лишь одна дверь. Эти условия можно задать
равенствами:![]() и
и![]() .
.![]() аналогично,
аналогично,![]() (представление в виде СДНФ или СКНФ).
Построим формулу:
(представление в виде СДНФ или СКНФ).
Построим формулу:![]()
![]()
![]()
Так как
![]() ,
то
,
то![]() аналогично,
аналогично,![]() ,
следовательно,
,
следовательно,![]() Мы получили тавтологию, следовательно,
рассуждения верны.
Мы получили тавтологию, следовательно,
рассуждения верны.
Пример 10.На предприятии есть три цеха:A,B,C, договорившиеся о порядке утверждения проектов, а именно:
1. Если цех Bне участвует в утверждении проекта, то в этом утверждении не участвует и цехA.
2. Если цех Bпринимает участие в утверждении проекта, то в нем принимают участие цехаAиC.
Спрашивается, обязан ли при этих условиях цех Cпринимать участие в утверждении проекта, когда в нем принимает участие цехA?
Решение.Логические переменные: «Аучаствует
в утверждении проекта» обозначим черезА, «Вучаствует в утверждении
проекта» –В, «Сучаствует в
утверждении проекта» –С. Посылки:![]()
![]() .
Утверждение
.
Утверждение![]() Надо выяснить, верны ли рассуждения,
т.е. выяснить будет ли тавтологией
формула:
Надо выяснить, верны ли рассуждения,
т.е. выяснить будет ли тавтологией
формула:![]()
![]()
![]() следовательно, рассуждения верны.
следовательно, рассуждения верны.
Пример 11.Перед судом стоят три человека, из которых каждый может быть либо туземцем, либо колониалистом. Судья знает, что туземцы всегда отвечают на вопросы правдиво, между тем как колониалисты всегда лгут. Однако судья не знает, кто из них туземец, а кто колониалист. Он спрашивает первого, но не понимает его ответа. Поэтому он спрашивает сначала второго, а потом третьего о том, что ответил первый. Второй говорит, что первый назвал себя туземцем. Третий говорит, что первый назвал себя колониалистом. Кем были второй и третий подсудимые?
Решение.Во-первых, если первый человек туземец, то он назовет себя туземцем, если он колониалист, то тоже назовет себя туземцем. Высказывание «первый сказал, что он туземец» обозначим черезx, «второй туземец» –y, «третий туземец» –z, и заметим, чтоx 1.
Имеем
![]() следовательно, второй – туземец.
следовательно, второй – туземец.![]() следовательно, третий – колониалист.
следовательно, третий – колониалист.
