3. Минимизация булевых функций

3.1. Минимизация нормальных форм

Минимальной ДНФ (МДНФ)функцииf(x₁, ... ,x_n) называется ДНФ, реализующая функциюfи содержащая минимальное число символов переменных по сравнению со всеми другими видами ДНФ, реализующими функциюf.

Если для всякого набора = (a₁, ...,a_n) значений переменных условиеg()=1 влечёт , то функцияgназывается частью функцииf(или функцияfнакрывает функциюg). Если при этом для некоторого набора= (c₁, ...,c_n) функцияg()=1, то говорят, что функцияgнакрывает единицу функцииfна наборе(или чтоgнакрывает конституенту единицы функцииf). Заметим, что конституента единицы функцииfесть часть функцииf, накрывающая единственную единицу функцииf.

Элементарная конъюнкция Kназывается импликантом функцииf, если для всякого набора =(a₁, ...,a_n) из 0 и 1 условиеK()=1 влечетf()=1.

Импликант Kфункцииfназывается простым, если выражение, получающееся из него выбрасыванием любых множителей, уже не импликант функцииf.

Ясно, что всякий импликант функции fесть часть функцииf.

Теорема. Всякая функция реализуется дизъюнкцией всех своих простых имликант (ПИ).

Доказательство.Пустьf(x₁, ...,x_n) есть функция, аA=K₁v ... v K_m – дизъюнкция всех ее простых импликант. Пусть = (a₁, ...,a_n) – произвольный набор длиныnиз 0 и 1.

Если A() = 1, то найдется дизъюнктивное слагаемоеK_i () = 1, что влечетf() = 1, ибоK_i есть импликант функцииf.

Если f() = 1, то в СДНФ для функцииfнайдется элементарная конъюнкцияK, равная на этом наборе единице. Один из простых имликантовK_jфункцииfполучается выбрасыванием некоторых множителей изKи потому K_j() = 1, а тогдаA() = 1.

Следовательно, f=A. Теорема доказана.

Сокращенная ДНФфункцииfесть дизъюнкция всех простых импликант функцииf. Всякая функцияfреализуется своей сокращенной ДНФ. Для всякой функции, не равной тождественно нулю, существует единственная сокращенная ДНФ.

Пусть AиB– произвольные формулы. Из свойств булевых операций вытекают следующие обратимые правила преобразования ДНФ:

1) – полное склеивание (развертывание);

2) – неполное склеивание;

3) – обобщенное склеивание;

4) – поглощение;

5) – идемпотентность ( удаление дублирующих членов).

Теорема ( Квайна ). Если в СДНФ функцииf провести все операции неполного склеивания, а затем все операции поглощения и удаления дублирующих членов, то в результате получится сокращения ДНФ функцииf.

Доказательство. Пусть имеем сокращенную ДНФ функцииf. Проведем все операции развертывания к каждому простому импликанту для получения недостающих переменных в каждом дизъюнктивном слагаемом сокращенной ДНФ. В полученном выражении из нескольких одинаковых дизъюнктивных слагаемых оставим только по одному экземпляру. В результате получим СДНФ функцииf. Теперь, исходя из полученной СДНФ, в обратном порядке проведем операции добавления одинаковых дизъюнктивных слагаемых (с помощью правил идемпотентности), неполного склеивания и поглощения. В итоге получим исходную сокращенную ДНФ.

Алгоритм Квайна построения сокращенной днф.

1. Получить СДНФ функции f.

2. Провести все операции неполного склеивания.

3. Провести все операции поглощения.

Пример 1.Построим сокращенную ДНФ для функции, приведенной в таблице 3.1.

Таблица 3.1

x y z t	0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
f	1 1 1 1 0 1 0 0 1 0 1 0 1 1 1 1

1. Строим СДНФ функции f:

. Пронумеруем дизъюнктивные члены в полученной СДНФ в порядке от 1 до 11.

2. Проводим все операции неполного склеивания.

Первый этап склеивания в таблице 3.2.

После первого этапа склеиваний (и возможных поглощений) получаем, что

Пронумеруем дизъюнктивные члены в полученной ДНФ в порядке их следования от 1 до 15.

Второй этап склеиваний в таблице 3.3.

После второго этапа склеиваний и последующих поглощений получаем, чтоЭто и будет сокращенной ДНФ для функцииf, ибо дальнейшие склеивания невозможны.

Таблица 3.2

Слагаемые	Склеивание по	Результат
1,2	T
1,3	Z
1,6	X
2,4	Z
2,5	Y
3,4	T
3,7	X
5,9	X
6,7	Z
6,8	Y
7,10	Y
8,9	T
8,10	Z
9,11	Z	xyt
10,11	T	xyz

Таблица 3.3

Слагаемые	Склеивание по	Результат
1, 6	Z
2, 4	T
2, 8	X
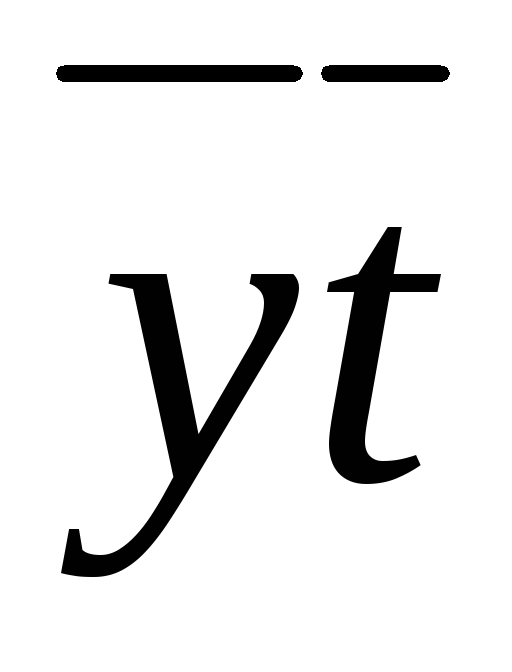
3, 7	Z
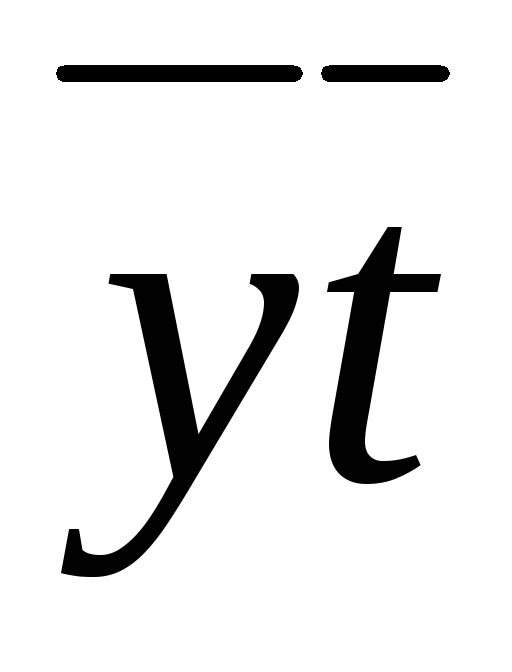
8, 13	Y	x
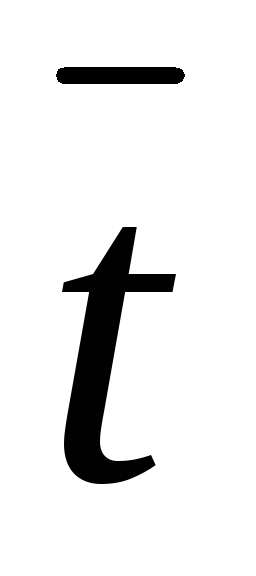
10, 11	Z	x
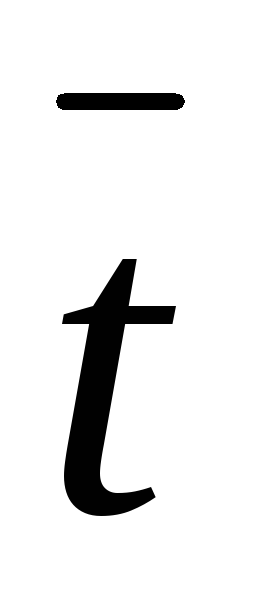
12, 15	Z	xy
13, 14	T	xy