
- •1.Решения
- •1. Решение на числовом промежутке
- •2. Задача Коши
- •3. Продолжение решений.
- •4. Общее решение.
- •5. Интегральная поверхность
- •6. Интегральная кривая, заданная неявно
- •7. Первый интеграл
- •8. Базис первых интегралов
- •2.Траектории
- •1. Траектория
- •3. Регулярные точки
- •4. Виды траекторий
- •5. Параметрическое задание траекторий
- •6. Неявное задание траекторий
- •7. Уравнение траекторий
- •7.Сложные состояния равновесия систем с линейными членами.
- •8. Признаки ограниченности числа предельных циклов.
- •10.Преобразование Бендиксона
- •13. Преобразование Пуанкаре.2
- •14. Круг Пуанкаре.
- •15. Типы диф. Сис-мы на проективной ф.П.
- •16. Поведение траекторий в окрестности экватора сферы Пуанкаре (s2 p)
- •17. Проективный атлас сферы Пуанкаре.
14. Круг Пуанкаре.
Объектом исследования является обыкновенная автономная дифференциальная система второго порядка
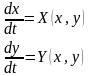 (I)
c
целыми правыми частями
(I)
c
целыми правыми частями
 на предмет глобального поведения
траекторий.
на предмет глобального поведения
траекторий.
Дифференциальную
систему (I)
будем рассматривать, когда целые функции
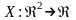 ,
,
 являются алгебраическими, т.е.
- полиномы с коэффициентами из поля
являются алгебраическими, т.е.
- полиномы с коэффициентами из поля
 .
.
Пусть
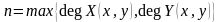 .
Правые части (I)
представим в виде
.
Правые части (I)
представим в виде
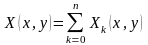 ,
,
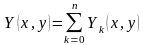 (1) где
(1) где
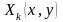 ,
,
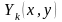 - однородные полиномы степени
- однородные полиномы степени
 при этом выполняется
при этом выполняется
 на
на
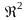 (2)
(2)
Говоря
о глобальном поведении траекторий
системы (I)
будем иметь в виду поведение траекторий
системы (I)
на всей фазовой пл-ти (х, у) с обязательным
изучением их поведения на бесконечность,
т.е.
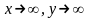 .
По необходимости различая случай
.
По необходимости различая случай
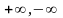 .
.
Мат-кую строгость с которой изучим глобальное поведение траекторий всякий раз будем устанавливать с точностью до некоторого преобразования. Это преобразование должно сохранять топологические инварианты принятия в локальной качественной обыкновенной автономной дифференциальной системе на плоскости.
При
проектировании ф. пл-ти (х,у) на S2P
каждой точке пл-ти (х,у) сопоставляются
две диаметрально противоположные точки
сферы, расположенные в южной и северной
полусферах, поэтому можно рассматривать
отображение ф. пл-ти на одну из полусфер:
южную или северную. Рассмотрим южную
полусферу вместе с экватором это
многообразие с краем обозначается
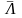 ,
тогда
,
тогда
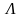 -
южная полусфера без экватора. А экватор
обозначим
-
южная полусфера без экватора. А экватор
обозначим
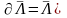 .
На экваторе расположены б. уд-ые точки
ф. пл-ти (х,у). Естественной проекцией
на ф. пл-ть яв-ся круг единичного радиуса
К с центром в начале координат О. Этот
круг К получил название круга
Пуанкаре
(рис.53.2).
Граничная окружность круга Пуанкаре
.
На экваторе расположены б. уд-ые точки
ф. пл-ти (х,у). Естественной проекцией
на ф. пл-ть яв-ся круг единичного радиуса
К с центром в начале координат О. Этот
круг К получил название круга
Пуанкаре
(рис.53.2).
Граничная окружность круга Пуанкаре
 является образом экватора
.
Круг Пуанкаре является моделью для
построения поведения траекторий в ф.
пл-ти дополненный б удми т-ми. Точки
расположенные в конечной части ф. пл-ти
отображаются в точки открытого круга
является образом экватора
.
Круг Пуанкаре является моделью для
построения поведения траекторий в ф.
пл-ти дополненный б удми т-ми. Точки
расположенные в конечной части ф. пл-ти
отображаются в точки открытого круга
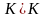 это отображение биективно. Б. уд-ые точки
ф. пл-ти (х,у) проектируются на граничную
окружность
при этом выполняются следующие
закономерности:
это отображение биективно. Б. уд-ые точки
ф. пл-ти (х,у) проектируются на граничную
окружность
при этом выполняются следующие
закономерности:
1) система координат Оху делит круг Пуанкаре на четыре части, нумеруем их в соответствии с нумерацией координатных углов. Говорят о I, II, III, IV четвертях круга Пуанкаре. Каждая точка i-ого координатного угла ф. пл-ти взаимно однозначно отображается в точку i-ой четверти круга Пуанкаре;
2)
прямая
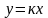 отображается на диаметр круга Пуанкаре
лежащий на этой прямой. Прямая
отображается на диаметр круга Пуанкаре
лежащий на этой прямой. Прямая
 отображается на диаметр расположенный
на оси Оу. У параллельных прямых будет
общая б. уд-нная точка. Прямая
отображается на диаметр расположенный
на оси Оу. У параллельных прямых будет
общая б. уд-нная точка. Прямая
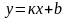 отображается на дуги с концами в точке
пересечения прямой
и круга Пуанкаре К. Прямые
отображается на дуги с концами в точке
пересечения прямой
и круга Пуанкаре К. Прямые
 отображаются на простые дуги, которые
опираются на диаметр расположенный на
оси Оу;
отображаются на простые дуги, которые
опираются на диаметр расположенный на
оси Оу;
3)
если прямая
является наклонной
 или горизонтальной к=0
асимптотой кривой γ при
или горизонтальной к=0
асимптотой кривой γ при
 или
или
 ,
то образ этой кривой γ на круге Пуанкаре
имеет граничную точку являющуюся точкой
пересечения окружности с лучом
;
,
то образ этой кривой γ на круге Пуанкаре
имеет граничную точку являющуюся точкой
пересечения окружности с лучом
;
4) образом простой замкнутой кривой расположенной в конечной части ф. пл-ти яв-ся простая замкнутая кривая целиком лежащая в открытом круге Пуанкаре.
Определение. Две системы вида (I) наз-ся эквивалентными на круге Пуанкаре, если существует диффеоморфизм их кругов Пуанкаре переводящие траектории одной системы в траектории другой.
В результате линейного невырожденного преобразования системы (I) получаем ее эквивалентную систему на круге Пуанкаре.
