90. Дифференциальные уравнения первого порядка. Общее и частное решения.

Линейное дифференциальное уравнение первого порядка имеет вид

a (x) y' + b (x) y + c(x) = 0,                         (1)   a (x) ¹ 0 .

Разделим обе части уравнения на a(x).

y' + p(x) y + q(x) = 0, где p(x) =     ,              q(x) =       (2).

Будем искать решения уравнения (2) в виде произведения двух неизвестных функций:

y = u·v.

Подставим y = u·v в (2)

,

                                     (3).

Выберем функцию u так, чтобы  :

,

,

,

,

.

Подставим полученную функцию u(х) в (3) и найдем n(х):

,

,

,

,

.

Подставим функции u(х) и n(х) в выражение для у:

 - общее решение линейного дифференциального уравнения первого порядка.

91. Уравнения с разделенными и разделяющимися переменными.

Дифференциальными уравнениями с разделяющимися переменными называют уравнения вида

X₁(x) Y₁(y)dx + X₂(x) Y₂(y)dy = 0.

Перенесем второе слагаемое в правую часть.

X₁(x) Y₁(y)dx = -X₂(x) Y₂(y)dy .

Предположим, что Y₁(y) X₂(x) ¹ 0. Разделим обе части уравнения на это произведение:

.

Переменные разделились. Интегрируя обе части этого равенства, получим общее решение уравнения:

.

92. Однородные уравнения первого порядка.

Однородным уравнением первого порядка называется уравнение вида

Заменой z = y/x это уравнение сводится к уравнению с разделяющимися переменными относительно функции z = z(x)

Пример:

Уравнение

как легко видеть, является однородным уравнением первого порядка:

Обозначим   z(x) = y(x)/x. Тогда   y(x) = x·z(x).

Подставив в уравнение и выполнив простые вычисления имеем уравнение с разделёнными переменными отнсительно функции z = z(x):

Вычислив соответствующие интегралы, легко получить решение этого последнего уравнения:

 

И, наконец, после обратной подстановки  z = y/x  имеем общий интеграл исходного однородного уравнения

или, что то же самое,

93. . Линейные однородные дифференциальные уравнения. Решение уравнения.

              

94. Уравнения в полных дифференциалах.

 1°.   Уравнение

                                    (7.1)

называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции  U (x, y) и следовательно его можно записать в виде:                                                                  

                                            dU=0    U=const=c  

Например, уравнение  xdy+ydx=0, есть уравнение в полных дифференциалах, так как его можно записать в виде d(xy)=0   и, значит,  xy=c.

Если функции M и N в области задания непрерывны и имеют частные производные соответственно по y и по  x, то для того чтобы уравнение  (7.1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество

 

                                                                                                               (7.2)

Если условие  (7.2) выполнено, то решение можно записать в виде

                                                                                     (7.3)

 либо                                      

                                                    ,                                (7.4)

где    – произвольная точка в области задания функций  M и N. 

         Частное решение, удовлетворяющее начальным условиям  , в случае когда функции M и N  не обращаются одновременно в 0 в точке   , можно найти обычным путем, определив константу c из общего решения, а можно в формулах  (7.3)  и  (7.4) положить  :

                                                                                  (7.5)

либо

                                                                                   (7.6)

 

П. 7.1              .

 

Проверяем выполнение условий  (7.2).    уравнение в полных дифференциалах. Полагаем   тогда    По формуле  (7.3)  находим   ,                              - общий  интеграл. 

 

П. 7.2              

Проверяем выполнение условий  (7.2).        уравнение в полных  дифференциалах. Полагаем   c=0, тогда    По формуле  (7..5)  находим

      ,                    

 

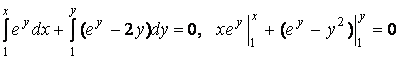2°. Существуют  уравнения  вида   (7.1)     , которые не являются уравнениями в полных дифференциалах, но после умножения обеих частей уравнения на некоторую функцию   получается уравнение в полных дифференциалах

                            

Функция     называется  интегрирующим множителем, а функция U соответствующим ему интегралом  уравнения (7.1).

Ясно, что если заданное уравнение уже является уравнением в полных дифференциалах, то  

Интегрирующий множитель должен удовлетворять уравнению с частными производны-ми :                                    (7.7)

Если  заранее известно, что   является  некоторой  функцией  от  ,  ,  где    заданная  функция от     то уравнение  (7.7) сводится к линейному уравнению относительно неизвестной функции   , зависящей от переменной  :

                                                     ,                                                                  (7.8)

где                                     .                                                           (7.9)

            Решив уравнение  (7.8), найдем интегрирующий множитель    .

В частности, если выполнено условие

                                       либо            ,             (7.10)

то интегрирующий множитель         либо        .

            П. 7.3           

Проверим, не имеет ли уравнение интегрирующий множитель, зависящий только от  x:

     

. Умножая  обе части исходного уравнения на     , получим:

                                       .

Легко проверить, что получено уравнение в полных дифференциалах. Действительно,

      . Далее,   ,

 - общий  интеграл.   

П. 7.4                    

Проверяем  выполнение условиий  (7.10):   ,

         , 

         Т.о.,    .  По формуле (7.3) при   имеем

  - общее решение.

П. 7.5              . Известно,  что    , 

найти интегрирующий множитель. По формуле  (7.9) находим:  

    

      .  

          П. 7.6       . Известно,  что    ,   

проинтегрировать уравнение. По формуле  (7.9) находим:

                  

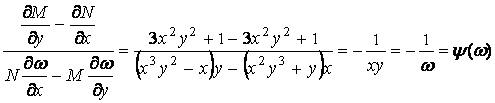
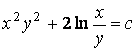   . Умножая  обе части исходного уравнения на   , получаем:    -  уравнение в полных дифференциалах.  По формуле  (7.3)  при   находим   ,   ,     - общий интеграл.  

          Следует иметь в виду, что при умножении обеих частей уравнения на интегриру-ющий множитель может появиться постороннее решение – точки кривой    .

          Замечание. Полезно обратить внимание на то, что уравнения с разделяющимися переменными, однородные, обобщенные однородные и уравнения в полных дифферен-циалах имеют одинаковый внешний вид.