
- •Определители и их св-ва.
- •Миноры и алгебраические дополнения
- •Методы вычисления определителей
- •Обратная матрица. Теорема о существ обратной матрицы.
- •Элементарные преобразования матрицы.
- •Ранг матрицы. Правило вычисления ранга матрицы.
- •Системы n линейных алгебраических уравнений с n неизвестными
- •Правило Крамера
- •Теорема Кронекера-Капелли.
- •Метод Гаусса.
- •Вектора. Коорд вектора в декартовой системе координат.
- •Направляющие косинусы вектора
- •Скалярное произведение векторов. Его свойства.
- •.Векторное произведение векторов. Его св-ва.
- •Смешанное произведения векторов
- •Общее уравнение плоскости
- •Уравн плоскости проходящей через три точки в отрезках
- •Параметрическое и каноническое уравнение прямой
- •Уравнение прямой, проходящей через 2 точки
- •Уравнением прямой с угловым коэффициентом k.
- •Угол между прямыми на плоскости.
- •Эллипс. Каноническое уравнение.
- •Каноническое уравнение гиперболы
- •Парабола. Каноническое уравнение.
- •Функция. Характеристики поведения. Сложная функция.
- •Пределы функций, их свойства.
- •Теоремы о пределах.
- •Первый замечательный предел.
- •Второй замечательный предел( показательно-степенной предел)
- •Непрерывность функции в точке. Свойства непрерывных функций.
- •Точки разрыва функции. Их классификации.
- •Производная функции, ее геометрический смысл.
- •Основные правила дифференцирования
- •Дифференцирование тригонометрических и обратных им функций.
- •Дифференцирование логарифмических, показательных и степенных функций
- •Логарифмическое дифференцирование
- •Дифференцирование обратных функций и функций заданных параметрически
- •Дифференциал функции. Геометрический смысл дифференциала.
- •Формула Тейлора.
- •Возрастание и убывание функций. Точки экстремума.
- •Необходимое условие существования экстремума.
- •Критические точки. Достаточные условия существования экстремума.
- •Исследование функции на экстремум с помощью производных высших порядков.
- •Выпуклость и вогнутость кривой. Точки перегиба.
- •Асимптоты.
- •Функции нескольких переменных (Определение, примеры).
- •Пределы функции нескольких переменных и их свойства
- •Частное и полное приращение функций нескольких переменных.
- •Непрерывность функции нескольких переменных их св-ва
- •Частные производные первого и высших порядков
- •Теорема о смешанных производных второго порядка
- •Полный дифференциал.
- •Касательная плоскость и нормаль к поверхности.
- •Формула Тейлора для функций нескольких переменных
- •Экстремум функции нескольких переменных.
- •Необходимые и достаточные условия существования безусловного экстремума.
- •Максимум и минимум функции нескольких переменных.
- •Первообразная.
- •Неопределенный интеграл и его свойства
- •Замена переменных в неопределенном интеграле
- •Простейшие приемы интегрирования. Интегрирование по частям.
- •Простейшие приемы интегрирования. Интегрирование способом замены переменной.
- •Разложение рациональных дробей на простейшие.
- •Интегрирование элементарных дробей.
- •Интегрирование рациональных функций
- •Интегрирование иррациональных функций.
- •Интегрирование тригонометрических функций
- •Задачи, приводящие к понятию определенного интеграла
- •Верхние и нижние интегральные суммы
- •Определенный интеграл, его свойства и простейшие методы интегрирования
- •Основные свойства определенного интеграла.
- •Геометрический и физический смысл определенного интеграла.
- •Формула Ньютона-Лейбница.
- •Приложения определенного интеграла к решению геометрических и механических задач.
- •1. Площадь плоской фигуры.
- •2. Площадь криволинейного сектора.
- •3. Объем тела вращения.
- •4. Длина дуги кривой.
- •5. Площадь поверхности вращения.
- •Вычисление работы сил
- •Несобственные интегралы первого рода
- •Несобственные интегралы второго рода
- •Длина дуги кривой.
- •Вычисление площадей в прямоугольных координатах.
- •Вычисление объема тела.
- •Объем тела вращения
- •Двойной интеграл.
- •Вычисление двойного интеграла
- •Классификация точек разрыва функции
- •Числовой ряд, сумма ряда.
- •Необходимое условие сходимости ряда.
- •Доказательство
- •Признаки сравнения. Признак Даламбера.
- •Признаки сравнения. Признак Коши.
- •Интегральный признак Коши
- •Интегральный сходимости знакопостоянных рядов.
- •Знакочередующийся ряд. Теорема Лейбница.
- •Степенной ряд. Теорема Абеля.
- •Интервал и радиус сходимости степенного ряда.
- •Дифференциальные уравнения первого порядка. Общее и частное решения.
- •Уравнения с разделенными и разделяющимися переменными.
- •Однородные уравнения первого порядка.
- •. Линейные однородные дифференциальные уравнения. Решение уравнения.
- •Уравнения в полных дифференциалах.
Частные производные первого и высших порядков
Частные
производные первого
порядка от
функции многих переменных
 обычно зависят от тех же переменных и
их можно ещё раз дифференцироватью
обычно зависят от тех же переменных и
их можно ещё раз дифференцироватью
Частными производными второго порядка называются частные производные от частных производных первого порядка
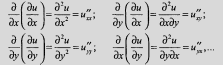
Частными производными третьего порядка называются частные производные от частных производных второго порядка

Частные производные других высших порядков определяются аналогично.
Теорема о смешанных производных второго порядка
Пусть
функция
![]() , и ее частные производные
, и ее частные производные
![]() определены в некоторой окрестности
точки
определены в некоторой окрестности
точки
![]() . Тогда предел
. Тогда предел
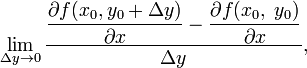 если он существует, называется смешанной
(смежной) производной функции
если он существует, называется смешанной
(смежной) производной функции
![]() в точке
и обозначается
в точке
и обозначается
![]() .
Аналогично определяется
.
Аналогично определяется
![]() как
как
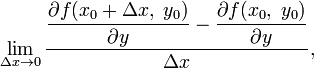 если он существует.
если он существует.
Рассматривая
частные производные
 и
и
 как функции от
как функции от
![]() , приходим к понятиям частных производных
второго порядка. А именно, выражения
, приходим к понятиям частных производных
второго порядка. А именно, выражения
 ,
,

называют
частными производными второго порядка
функции
![]() по х и по у соответственно, а выражения
по х и по у соответственно, а выражения
 ,
,

– смешанными
частными производными второго порядка
функции
.
Их обозначают также символами:
![]() ,
,
![]() ,
,
![]() и
и![]() . Аналогично определяют частные
производные 3-го порядка (их будет 8=23
), 4-го порядка (их будет 16=24
) и т.д.
. Аналогично определяют частные
производные 3-го порядка (их будет 8=23
), 4-го порядка (их будет 16=24
) и т.д.
Теорема
: Если в некоторой окрестности точки
![]() функция
функция
![]() имеет смешанные частные производные
имеет смешанные частные производные
 и
и , причем эти производные непрерывны в
точке М0
, то они равны в этой точке:
, причем эти производные непрерывны в
точке М0
, то они равны в этой точке:
 =
=
 .
.
Если последнее равенство выполняется, то говорят, что смешанные частные производные 2-го порядка функции не зависят от порядка дифференцирования в точке М0.
Обозначение :
![]()
![]()
Теорема Шварца:
Пусть выполнены условия:
Функции
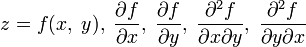 определены в некоторой окрестности
точки
.
определены в некоторой окрестности
точки
.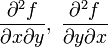 непрерывны в
точке
.
непрерывны в
точке
.
Тогда
![]() ,
то есть смешанные производные второго
порядка равны в каждой точке, где они
непрерывны.
,
то есть смешанные производные второго
порядка равны в каждой точке, где они
непрерывны.
Теорема Шварца о равенстве смешанных частных производных индуктивно распространяется на смешанные частные производные высших порядков, при условии, что они непрерывны.
Пример
 смешанные
производные второго порядка равны
всюду кроме точки (0,0), в которой и
нарушается равенство смешанных
производных.
смешанные
производные второго порядка равны
всюду кроме точки (0,0), в которой и
нарушается равенство смешанных
производных.
Полный дифференциал.
Полное приращение функции 2-х переменных
Если обеим переменным дать приращение, то функция получит полное приращение

Определение дифференцируемой функции
Ф ункция
называется дифференцируемой
в точке М(х,у), если ее полное
приращение можно представить в виде
ункция
называется дифференцируемой
в точке М(х,у), если ее полное
приращение можно представить в виде
,

 где Δx
и Δy
-произвольные приращения аргументов
х и у в некоторой окрестности точки
М(х,у), А и В –постоянные, независящие
от Δx
и Δy ,
o(ρ)-бесконечно
малая более высокого порядка, чем
-расстояние между
М(х,у) и
где Δx
и Δy
-произвольные приращения аргументов
х и у в некоторой окрестности точки
М(х,у), А и В –постоянные, независящие
от Δx
и Δy ,
o(ρ)-бесконечно
малая более высокого порядка, чем
-расстояние между
М(х,у) и
О пределение
дифференциала
пределение
дифференциала
Главная линейная относительно Δx и Δy часть полного приращения функции
 называется
полным дифференциалом этой функции
и обозначается dz или
df(x,y)
. Таким образом,
называется
полным дифференциалом этой функции
и обозначается dz или
df(x,y)
. Таким образом,
Ф ормула для вычисления дифференциала
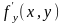
 Если функция дифференцируема
в точке М(х,у),то она имеет в этой точке
частные производные и
, причем первое =В, а второе В
Если функция дифференцируема
в точке М(х,у),то она имеет в этой точке
частные производные и
, причем первое =В, а второе В
Т

 аким
образом
Если положить
,то
аким
образом
Если положить
,то
