43. Исследование функции на экстремум с помощью производных высших порядков.

Пусть в точке х = х₁ f¢(x₁) = 0 и f¢¢(x₁) существует и непрерывна в некоторой окрестности точки х₁.

Теорема. Если f¢(x₁) = 0, то функция f(x) в точке х = х₁ имеет максимум, если f¢¢(x₁)<0 и минимум, если f¢¢(x₁)>0.

Доказательство. Пусть f¢(x₁) = 0 и f¢¢(x₁)<0. Т.к. функция f(x) непрерывна, то f¢¢(x₁) будет отрицательной и в некоторой малой окрестности точки х₁. Т.к. f¢¢(x) = (f¢(x))¢ < 0, то f¢(x) убывает на отрезке, содержащем точку х₁, но f¢(x₁)=0, т.е. f¢(x) > 0 при х<x₁ и f¢(x) < 0 при x>x₁. Это и означает, что при переходе через точку х = х₁производная f¢(x) меняет знак с “+” на “-“, т.е. в этой точке функция f(x) имеет максимум.Для случая минимума теорема доказывается аналогично. Если f¢¢(x) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.

44. Выпуклость и вогнутость кривой. Точки перегиба.

Для описания свойств графиков функций используется понятие направления выпуклости.

Определение.График дифференцируемой функции y= f (x) называется выпуклым (вниз вверх) на интервале (a, b),если на этом интервале он расположен выше/ниже любой своей касательной.

График, выпуклый вверх называют просто выпуклым, а выпуклым вниз – вогнутым.

Определение. Точка графика непрерывной функции, отделяющая его части с разным направлением выпуклости называется точкой перегиба.

Итак, интервалы выпуклости находятся с помощью следующей теоремы.

Теорема. Если f′′( x)< 0 на интервале (а, b), то график функции y= f (x) на этом интервале имеет выпуклость вверх. Если f′′( x) >0 на интервале (а, b), то график функции y= f (x) на этом интервале имеет выпуклость вниз.

Заметим, что при этом в отдельных точках вторая производная может обращаться в нуль.

Теорема ( необходимое условие перегиба). Если х0 – абсцисса точки перегиба графика функции y= f (x), то в этой точке вторая производная равна нулю или не существует.

При этом все точки, принадлежащие области определения функции, в которых вторая производная этой функции равна нулю или не существует называются критическими точками второго рода. Только такие точки могут быть абсциссами точек перегиба. Теорема (достаточной условие существования перегиба).

Если вторая производная функции f′′( x) при переходе через точку х=0, в которой она равна нулю или не существует, меняет знак, то точка с абсциссой х=0 является точкой перегиба.

45. Асимптоты.

Асимптоты -  прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат (например ctg и tg)

Пример:

  Рассмотрим график  . При   график приближается к горизонтальной асимптоте  , а при   -- к другой горизонтальной асимптоте  . 

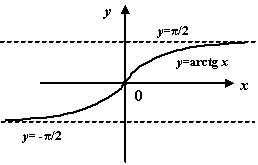
Виды асимптот графиков:

Вертикальная асимптота — прямая вида   при условии существования предела  .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1. 

2. 

Горизонтальная асимптота — прямая вида   при условии существования предела. .

Наклонная асимптота —  прямая  вида   при условии существования предела функции

1. 

Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен  ), то наклонной асимптоты при  (или  ) не существует!