14.Сформулируйте задачу использования ресурсов и напишите ее математическую модель.
Для изготовления продукции вида P1, P2.. Pn используется m-видов сырья, S1,S2 .. Sm.Расход каждого вида сырья на изготовление единицы каждого вида продукции задана таблицей (технологической картой).
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Количество сырья, имеющегося на складе (запас)-составляет B1. Стоимость единицы продукции Cj- цена Pj.Xj-кол-во продукции, которое нужно найти. Необходимо составить оптимальный план производства, позволяющий получить прибыль в рамках существующих ограничений.
1
.F=C1X1+C2X2+CnXn
max,
2. xj>=0 (j=1,2,n),
3. a11x1+a12x2+…a1nxn<=b1
a21x1+a22x2+…a2nxn<=b2
am1x1+am2x2+amnxn<=bm
Такая задача называется стандартной задачей max (в системе ограничений (3) знак только <=)
15.Сформулируйте задачу составления рациона и напишите ее математическую модель.
Имеется n видов продуктов P1 , P2 , ... Pn , содержащих питательные вещества S1 , S2 , ... Sm . Необходимый минимум потребления этих питательных веществ составляет b1 , b2 , ... bm . В одной единицы продукта Pj содержится питательное вещество Si в количестве aij . Стоимость одной единицы продукта Pj равна c j . Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательного вещества было бы не менее установленного предела.
Обозначим через x j количество продукта Pj ( j 1, 2, ..., n ), входящего в рацион. Стоимость рациона будет равна c1x1 c2 x2 ... cn xn . Количество питательного вещества Si в рационе составит ai1x1 ai2 x2 ... ain xn . Это количество не должно быть меньше необходимого минимума bi . Следовательно, переменные x1, x2 , ..., xn должны удовлетворять условиям
(1)
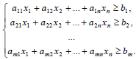
Теперь можем сформулировать математическую
модель задачи составления рациона:
найти неотрицательные значения переменных
x1, x2 , ..., xn , удовлетворяющие системе
неравенств (1),при которых ф-я
принимает
минимальное значение.
Мы видим, что две различных по содержанию задач привели нас к очень похожим
математическим моделям. Они отличаются лишь знаками неравенств в системе неравенств и тем, что в первом случае требуется найти максимум функции L , а во втором минимум. Однако, эти различия не являются существенными, так как знак неравенства можно заменить на противоположный, умножив это неравенство на (-1), а задачу отыскания минимума функции L можно свести к отысканию максимума функции L= - L .
Задача отыскания неотрицательных значений переменных x1, x2 , ..., xn , довлетворяющих
системе неравенств
(2)
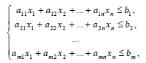
При которых функция
(3)
принимает оптимальное (максимальное или минимальное значение) называется стандартной задачей линейного программирования.
Система (5) называется системой ограничений или системой балансовых условий, а
функция L — целевой функцией. Множество точек (x1, x2 , ..., xn ) n -мерного пространства,
удовлетворяющих системе неравенств (2) и условию x j ≥ 0 , j =1, 2, ..., n , называют областью допустимых значений.
Формулы (2) и (3) можно записать более кратко, используя знак суммы:
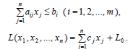
Используют также матричную запись этих соотношений:
где {А}= aij — матрица размерности m ><n , X= (x1, x2 , ..., xn )^T — n -мерный вектор-столбец, b= (b1 ,b2 , ..., bm )^T — m -мерный вектор столбец, c = (c1, c2 , ..., cn )— n -мерный вектор-строка.
Вектор X (x1, x2 , ..., xn )^T , при котором целевая функция достигает оптимального
значения, называется оптимальным решением задачи линейного программирования, если его компоненты удовлетворяют системе ограничений (2) и условию неотрицательности переменных x j ≥ 0 , j =1, 2, ..., n .