27.Матричная игра двух сторон с нулевой суммой. Чистые, смешанные, оптимальные стратегии, цена игры.

28.Точные формулы решения игры в терминах решений вспомогательной пары двойственных ЗЛП (теорема Неймана).

Теорема Неймана - каждая матричная игра имеет по крайней мере одно решение, к-м может быть определенная смешанная стратегия.

Приведение матричной игры к ЗЛП

1.Преобразование платежной матрицы к ЗЛП. Все элементы матрицы д.б. неотриц. A’=A+C – новая матрица без отриц. элементов. А- исходная матрица. С-const.

Цена игры увеличивается на C, но оптимальные стратегии не изменятся.

V’=V+3; V=V’-3

2.Формирование двойственной задачи.

F =x1+x2+x3 max G=y1+y2 min

A11x1+a12x2+a1x3<=1 y1>=0

A22x2+a22x2+a23x3<=1 y2>=0

X1>=0 a11y1+a21y2>=1

X2>=0 a12y1+a22y2>=1

X3>=0 a13y1+a23y3>-1

Оптимальная стратегия игрока P

P*=(p*1,p*2) должна обеспечить первому игроку при любых ходах противника выигрыш не менее цены игры V.

P* A=V

(P*1,p*2) (a11 a12 a13)=P*1a11+p*2a21>=V

a21 a22 a23 P*1a12+P*2a22>=V

P*1a13+P*2a23>=V

Обе части нер-ва делим на V:

P*1a11/v +P*2a21/v>=1 задача 1-го игрока min

Введем обозначение Yi=Pi*/v

A11y1+a21y2>=1

Задача min в паре двойственных задач состоит в игре 1-го игрока P, тогда полученная в результате применения симплекс-метода целевая ф-я G(y) будет связана со значением цены игры V след. Образом

V=1/G(y*)

Пересчет стратегий:

Оптимальный план ЗЛП y* пересчитаем в оптимальную стратегию первого игрока p*=V’y*,

Аналогично для второго игрока Q, V=1/f(x*)

Стратегия Q*=V’x*

Ответ

V*=V’-C

P*= V’y*,

Q*=V’x*

Критерий оптимальности стратегий: M(Pi,Q*)<=V<=M(P*,Qj)

29.Доминирование строк и столбцов платежной матрицы и решение игры после упрощения матрицы.

30. Сформулируйте задачу целочисленного программирования и напишите ее математическую модель.

Целочисленная задача- такая задача, имеющая доп. ограничения на переменную xj-целое число.

(9)

‑ целые

31.Метод отсечение Гомори – нахождение целочисленного оптимального плана задачи линейного программирования, построение дополнительного ограничения (неравенства Гомори)

Определение оптимального плана задачи целочисленного программирования. Рассмотрим задачи целочисленного программирования, в которых как целевая функция, так и функции в системе ограничений являются линейными. В связи с этим сформулируем основную задачу линейного программирования, в которой переменные могут принимать только целые значения. В общем виде эту задачу можно записать так: найти максимум функции

(78)

при условиях

(79)

(80)

– целые  (81)

Если найти решение задачи (78) – (81) симплексным методом, то оно может оказаться как целочисленным, так и нет (примером задачи линейного программирования, решение которой всегда является целочисленным, служит транспортная задача). В общем же случае для определения оптимального плана задачи (78) – (81) требуются специальные методы. В настоящее время существует несколько таких методов, из которых наиболее известным является метод Гомори, в основе которого лежит описанный выше симплексный метод.

Метод Гомори. Нахождение решения задачи целочисленного программирования методом Гомори начинают с определения симплексным методом оптимального плана задачи (78) – (80) без учета целочисленности переменных. После того как этот план найден, просматривают его компоненты. Если среди компонент нет дробных чисел, то найденный план является оптимальным планом задачи целочисленного программирования (78) – (81). Если же в оптимальном плане задачи (78) – (80) переменная  принимает дробное значение, то к системе уравнений (79) добавляют неравенство

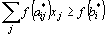8. (82)

и находят решение задачи (78) – (80), (82).

В неравенстве (82)  и  – преобразованные исходные величины  и  значения которых взяты из последней симплекс–таблицы, а  и  –дробные части чисел (под дробной частью некоторого числа а понимается наименьшее неотрицательное число b такое, что разность между аи b есть целое). Если в оптимальном плане задачи (78) – (80) дробные значения принимают несколько переменных, то дополнительное неравенство (82) определяется наибольшей дробной частью.

Если в найденном плане задачи (78) – (80), (82) переменные принимают дробные значения, то снова добавляют одно дополнительное ограничение и процесс вычислений повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования (78) – (81), либо устанавливают ее неразрешимость.

Если требование целочисленности (81) относится лишь к некоторым переменным, то такие задачи называются частично целочисленными. Их решение также находят последовательным решением задач, каждая из которых получается из предыдущей с помощью введения дополнительного ограничения. В этом случае такое ограничение имеет вид

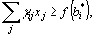8. (83)

где  определяются из следующих соотношений:

1) для  , которые могут принимать нецелочисленные значения,

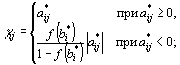8. (84)

2) для  , которые могут принимать только целочисленные значения,

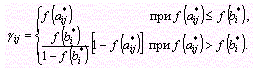8. (85)

Из изложенного выше следует, что процесс определения оптимального плана задачи целочисленного программирования методом Гомори включает следующие основные этапы:

1. Используя симплексный метод, находят решение задачи (78) – (80) без учета требования целочисленности переменных.

2. Составляют дополнительное ограничение для переменной, которая в оптимальном плане задачи (78) – (80) имеет максимальное дробноезначение, а в оптимальном плане задачи (78) – (81) должна быть целочисленной.

3. Используя двойственный симплекс–метод, находят решение задачи, получающейся из задачи (78) – (80) в результате присоединения дополнительного ограничения.

4. В случае необходимости составляют еще одно дополнительное ограничение и продолжают итерационный процесс до получения оптимального плана задачи (78) – (81) или установления ее неразрешимости.