
- •Сравнение естественного и стандартного чисел обусловленности матрицы а также - точного значения стандартного числа обусловленности с его оценкой, вычисленной процедурой decomp:
- •Исследовать возможность улучшения обусловленности задачи посредством внесения малого случайного возмущения в матрицу системы.
- •7 Повторить эксперимент п.6 для 2-3 задач с плохо обусловленной матрицей.
- •8 Выполняя п.П. 6 и 7 , исследовать работоспособность различных методов оценки ошибок решения ( выражения (7), (12), (13) ) при наличии возмущения левой части системы.
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные данные:
- •Исходные данные:
- •Провести исследование влияния вида доминирования матрицы задачи на сходимость процедур Якоби и Гаусса-Зейделя.
- •Исходные данные:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исследовать устойчивость решения задачи среднеквадратичного приближения к погрешности исходных данных.
- •Исходные параметры:
- •Убедиться в справедливости условий чебышевского интерполирования.
- •Исходные параметры:
- •При интегрировании нескольких систем нелинейных уравнений обратить внимание на эффективность различных методов реализации схемы прогноз-коррекция.
- •Исходные параметры:
- •Исходные параметры:
- •При интегрировании жёстких задач:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Дополнительное исследование метода релаксации:
Исходные параметры:
Порядок полинома: 4
Функции:
Метод: Ньютона
Интервал:
Сетка: равномерная.
-
Возмущение,
%
Узловая
координата
Уклонение
MaxEps(X )
0
X[1]= -1.0
X[2]= -0.5
X[3]= 0.0
X[4]= 0.5
X[5]= 1.0
Eps[1]= 0
Eps[2]= 0
Eps[3]= 0
Eps[4]= -2.22E-16
Eps[5]= -8.88E-16
1.83E-05 (-0.85)
1
X[1]= -1.0
X[2]= -0.5
X[3]= 0.0
X[4]= 0.5
X[5]= 1.0
Eps[1]= -9.40E-04
Eps[2]= -3.28E-03
Eps[3]= -2.38E-04
Eps[4]= 3.31E-03
Eps[5]= -5.90E-03
4.52E-03 (-0.7)
5
X[1]= -1.0
X[2]= -0.5
X[3]= 0.0
X[4]= 0.5
X[5]= 1.0
Eps[1]= 1.59E-02
Eps[2]= -6.46E-03
Eps[3]= -1.26E-02
Eps[4]= -3.17E-02
Eps[5]= 2.53E-03
3.20E-02 (0.55)
10
X[1]= -1.0
X[2]= -0.5
X[3]= 0.0
X[4]= 0.5
X[5]= 1.0
Eps[1]= -6.00E-02
Eps[2]= 7.88E-02
Eps[3]= -5.05E-02
Eps[4]= 2.00E-02
Eps[5]= -2.20E-04
6.00E-02 (-1.0)
15
X[1]= -1.0
X[2]= -0.5
X[3]= 0.0
X[4]= 0.5
X[5]= 1.0
Eps[1]= -1.24E-01
Eps[2]= 1.37E-01
Eps[3]= 1.08E-01
Eps[4]= 4.85E-02
Eps[5]= -9.15E-02
2.00E-01 (-0.7)
30
X[1]= -1.0
X[2]= -0.5
X[3]= 0.0
X[4]= 0.5
X[5]= 1.0
Eps[1]= -2.00E-01
Eps[2]= 1.20E-02
Eps[3]= 2.50E-01
Eps[4]= -1.41E-01
Eps[5]= 2.41E-01
2.62E-01 (-0.075)
50
X[1]= -1.0
X[2]= -0.5
X[3]= 0.0
X[4]= 0.5
X[5]= 1.0
Eps[1]= -1.33E-01
Eps[2]= 2.22E-01
Eps[3]= -4.17E-01
Eps[4]= 3.96E-01
Eps[5]= -2.34E-01
6.60E-01 (0.725)
75
X[1]= -1.0
X[2]= -0.5
X[3]= 0.0
X[4]= 0.5
X[5]= 1.0
Eps[1]= -3.23E-01
Eps[2]= -6.84E-01
Eps[3]= -6.46E-01
Eps[4]= -5.18E-01
Eps[5]= 4.92E-01
6.85E-01 (-0.475)
100
X[1]= -1.0
X[2]= -0.5
X[3]= 0.0
X[4]= 0.5
X[5]= 1.0
Eps[1]= 3.20E-01
Eps[2]= -6.73E-02
Eps[3]= -6.06E-02
Eps[4]= 1.85E-01
Eps[5]= -3.31E-02
7.60E-01 (-0.275)
Для обеих сеток внесение малейшего возмущения (1%) значительно ухудшает точность решения (в эксперименте для чебышёвской сетки погрешность увеличилась на 3 порядка, для равномерной – на 2). Дальнейшее усиление возмущения лишь немногим более ухудшает задачу (на 3-5 порядков в соответствии с экспериментом). Таким образом, можно сделать следующий вывод: независимо от типа сетки, решение задачи интерполирования является неустойчивым к погрешности исходных данных.
Исследование среднеквадратичного приближения функций.
Для двух функций, монотонной и имеющей экстремум на интервале приближения, решить задачу приближения полиномами 2-й, 3-й, 4-й и максимально достижимой степени; обратить внимание на изменение значения числа обусловленности матрицы нормальной системы уравнений от ее порядка; при двух различных порядках приближающего полинома исследовать зависимость погрешности решения (равномерной и среднеквадратичной) от величины массива исходных данных.
Исходные параметры:
Интервал:

Функции: - имеет экстремум на рассматриваемом промежутке;
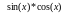 - не имеет
экстремума на рассматриваемом
промежутке;
- не имеет
экстремума на рассматриваемом
промежутке;
Метод: Средних квадратов
Число точек дискретизации диапазона: 100
-
Порядок
полинома
Обуслов-
леность
матрицы
Макс. уклонение
(равномерное)
Макс. уклонение
(среднеквадратичное)
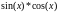
2
1.788E+02
1.11E-04
3.01E-02
4.81E-05
1.59E-02
3
2.776E+03
1.11E-04
4.57E-04
5.47E-05
1.96E-04
4
4.452E+04
1.83E-07
4.57E-04
7.67E-08
2.14E-04
7
-
-
-
-
-
16
-
-
-
-
-
С увеличением порядка полинома обусловленность матрицы задачи растёт; при определённом порядке полинома (в данном эксперименте при n=7) матрица задачи вырождается, что не даёт возможности исследовать полиномы этого и более высоких порядков.
Исследование зависимости погрешности решения от величины массива исходных данных.
