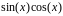1. Убедиться в справедливости условий чебышевского интерполирования.

Исходные параметры:

Интервал:

Метод: Чебышёвское интерполирование

Порядок полинома: 4

Функция	Чебышёвская сетка		Равномерная сетка
	координата	уклонение	координата	уклонение
	-0.951056	7.81E-04	-1.0	7.58E-04
	-0.587785	-7.81E-04	-0.5	-7.58E-04
	6.12E-17	7.81E-04	0.0	7.58E-04
	0.587785	-7.81E-04	0.5	-7.58E-04
	0.951056	7.81E-04	1.0	7.58E-04

Полученные данные свидетельствуют о выполнении необходимого и достаточного условия чебышёвского интерполирования: функция уклонения в узлах имеет одинаковые значения и противоположные знаки.

2. Решить задачу наилучшего равномерного приближения для функций, использованных в эксперименте 1 исследования среднеквадратичного приближения функций; установить возможность построения полинома максимально высокого (в пределах, допускаемых программой) порядка; сравнить точность решений задач приближения, полученных в п.1 исследования среднеквадратичного приближения и текущем пункте, по равномерному и среднеквадратичному критериям.

Исходные параметры:

_{Интервал:}

_Функции: - имеет экстремум на рассматриваемом промежутке;

- не имеет экстремума на рассматриваемом промежутке

Метод: Чебышёвское интерполирование

Порядок полинома
	Макс. равномер- ное уклонение		Макс. средне- квадратичное уклонение		Макс. равномер- ное уклонение			Макс. средне- квадратичное уклонение
	Ч*	Р			Ч*	Р
2	6.47E-05	1.02E-04		6.33E-05		2.75E-02	2.06E-02		1.23E-02
3	9.91E-05	8.05E-04		4.95E-05		2.51E-04	4.51E-04		2.40E-04
4	9.64E-08	2.13E-07		9.78E-08		4.08E-04	3.82E-04		2.03E-04
7	1.54E-10	2.63E-10		9.22E-11		5.27E-09	2.53E-08		8.57E-09
10	2.22E-16	2.22E-16		8.34E-17		2.40E-11	8.67E-11		2.51E-11
16	2.22E-16	8.44E-15		1.83E-15		2.22E-16	6.66E-16		1.14E-16

Построение полинома максимального (в допускаемых программой пределах) порядка возможно; более того: с увеличением порядка полинома значительно возрастает точность решения. Это связано со способом построения полинома наилучшего приближения: в связи с минимизацией квадрата максимального уклонения полинома от приближаемой функции происходит предотвращение возможности значительных локальных ошибок (отсутствия которых не гарантирует метод средних квадратов). Эта особенность построения и делает возможным увеличение точности с ростом порядка полинома наилучшего приближения (в отличие от метода средних квадратов, где при относительно небольших порядках полинома ошибка была столь высока, что программа не могла завершить выполнение алгоритма). Следует также отметить, что различие точности приближения имеющей и не имеющей экстремума функции (при малых порядках полинома последняя приближается менее точно) с увеличением степени полинома практически исчезает.

_____________________________________________________________________________________

*Ч – чебышёвская сетка, Р - равномерная

3. Установить степень близости решений, полученных в предыдущем пункте, с решениями задачи интерполирования на равномерной и чебышевской сетках (при одинаковых интервалах приближения и порядках приближающих полиномов).

Исходные параметры:

Интервал: - симметричный промежуток

_Функции: - чётная функция

Порядок полинома: 7

Метод Лагранжа:

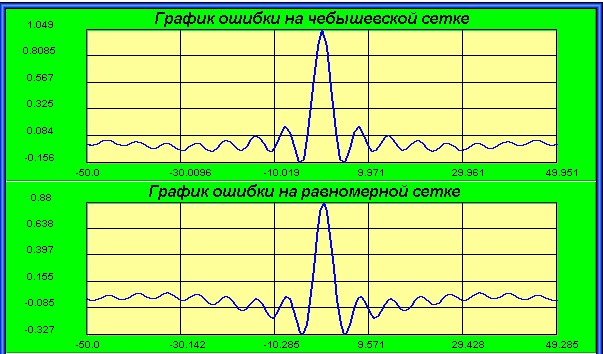
Метод Ньютона:

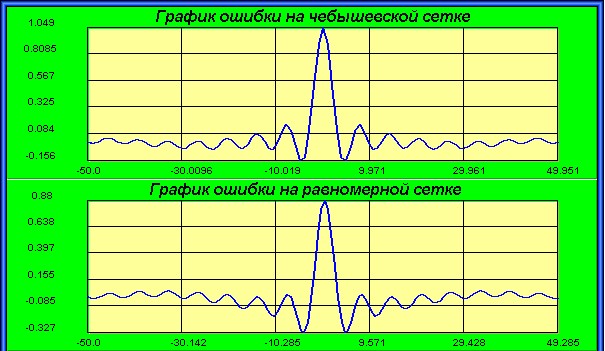
Чебышёвское интерполирование

Для достижения одинаковой точности метод чебышёвского интерполирования требует на единицу меньшего, чем методы Лагранжа и Ньютона, порядка полинома.

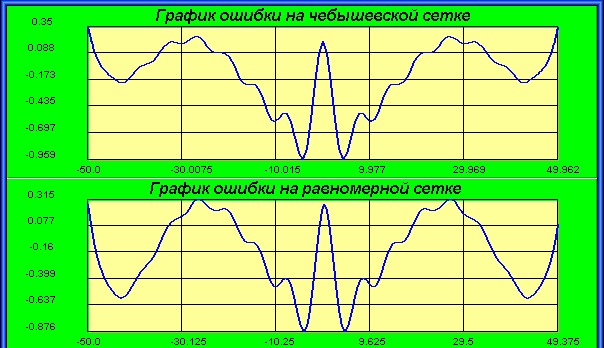
4. Исследовать устойчивость решения задачи равномерного приближения к ошибкам исходных данных.

Исходные параметры:

Интервал:

_Функции:

Метод: Чебышёвское интерполирование

Порядок полинома: 3

Возму- щение, %	Макс. уклонение (равномерное)			Макс. уклонение (среднеквадратичное)
	Ч*	Р
0	1.54E-03	1.25E-03		7.70E-04
1	9.10E-03	5.56E-03		2.32E-03
2	1.60E-02	1.55E-02		9.30E-03
5	3.27E-02	3.00E-02		1.80E-02
10	6.47E-02	6.01E-02		4.91E-02
15	6.89E-02	6.67E-02		3.98E-02
30	2.31E-01	2.17E-01		1.51E-01
50	5.33E-01	5.24E-01		3.26E-01
75	7.08E-01	6.75E-01		4.52E-01
100	8.57E-01	7.01E-01	2.90E-01

Сравнивая полученные данные с соответствующими данными для среднеквадратичного приближения, нетрудно видеть, что равномерное приближение функции является более устойчивым методом (при малых возмущениях превосходство возмущённых уклонений над невозмущёнными находилось в пределах порядка; с ростом вносимого возмущения различие уклонений росло и при максимальном возмущении в данном эксперименте эта разница достигла двух порядков).

Численные методы решения обыкновенных дифференциальных

уравнений.

6. При интегрировании нескольких систем линейных уравнений на основе информации о значениях собственных чисел матрицы системы оценить максимальную величину шага устойчивого интегрирования и проверить эту оценку экспериментально. Зафиксировать величину шага, при которой метод теряет устойчивость.

№ задачи	Собсвтвен- ные числа		Шаг
			Явн. Эйлера		Неявн. Эйлера			Трапеции
	Re	Im	*
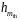1	-1	1	1	1
	-1	-1
2	-1	0	0.(2)	0.22
	-9	0
3	-1	0	2е-3	2е-3
	-1е+3	0
5	0	1	0	-					-
	0	-1
6	0	1	0
	0	-1

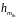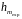* , - предельно допустимые теоретическое и экспериментальное значения шага устойчивого

интегрирования соответственно.

Как и ожидалось, при 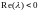неявный метод Эйлера и метод трапеции сохраняют устойчивость для любого шага. Для явного метода Эйлера теоретические предпосылки также подтвердились: для тех 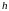, которых справедливо неравенство:

,

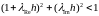устойчивое интегрирование сохранялось.

Другая ситуация возникла на границах областей устойчивости (задачи 5 и 6): ожидаемые результаты были опровергнуты для метода трапеции при решении задачи 5 и для явного метода Эйлера при решении задачи 6. Это несоответствие можно объяснить ошибками дискретизации: действительно, для данных задач область устойчивости явного метода Эйлера определяется неравенством , что соответствует одной точке из области устойчивости на плоскости (точке (0,0)); уравнение 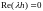соответствует прямой, разграничивающей области устойчивости метода трапеции. Ошибка дискретизации могла привести к смещению с границы как в область устойчивости, так и в область неустойчивости, чем и объясняется несоответствие с ожидаемыми результатами. Стоит также отметить, что для неявного метода Эйлера точка (0,0) также является граничной; однако область устойчивости здесь задана уравнением , поэтому при возможно появление подобного рода ошибки (в эксперименте были проверены значения , при которых ожидаемые результаты подтвердились).