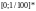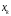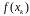Исходные параметры:

Задача №4 (линейная)

_{Интервал:}

Максимально допустимое время интегрирования: 180 сек

;

Ерs	Установ-ленная точность	Метод Гира (2-ого порядка)			Метод трапеций по схеме ПК с итер. Ньютона
		Фактическая точность	Время, с	Фактическая точность		Время, с
1е-4	1е-3	3е-3	3	2е-7		30
	1е-5	5е-4	3	-		>180
	1е-7	2е-5	5	-		>180
	1е-10	4е-7	18	-		>180
	1е-12	2е-7	21	-		>180
1е-5	1е-3	4е-9	3	3е-11		118
	1е-5	2е-10	4	-		>180
	1е-7	2е-9	7	-		>180
	1е-10	6е-10	17	-		>180
	1е-12	8е-10	20	-		>180
1е-6	1е-3	2е-8	2	-		>180
	1е-5	3е-10	3	-		>180
	1е-7	4е-9	5	-		>180
	1е-10	5е-10	15	-		>180
	1е-12	6е-10	20	-		>180

* - Для сохранения работоспособности программы и продолжения исследования интервал был изменён.

Исходные параметры:

Задача №11 (нелинейная)

_{Интервал:}

Ерs	Установ-ленная точность	Метод Гира (2-ого порядка)			Метод трапеций по схеме ПК с итер. Ньютона
		Фактическая точность	Время, с	Фактическая точность		Время, с
1е-4	1е-3	1е-3	1	6е-5		4
	1е-5	1е-4	2	1е-6		20
	1е-7	7е-6	7	-		>180
	1е-10	6е-7	14	-		>180
	1е-12	5е-7	18	-		>180
1е-8	1е-3	1е-3	1	6е-5		4
	1е-5	1е-4	2	1е-6		20
	1е-7	7е-6	7	-		>180
	1е-10	5е-7	14	-		>180
	1е-12	5е-7	18	-		>180

Экспериментальные данные показывают, что рассматриваемые методы с разной скоростью достигают одной фактической точности: метод Гира 2-ого порядка во много раз превосходит по скорости метод трапеций по схеме ПК с итерациями Ньютона. К тому же, в данном эксперименте метод Гира точность, отличающуюся от заданной не более, чем на порядок. Таким образом, можно заключить, что метод Гира 2-ого порядка с возможностью регулирования точности является более предпочтительным для решения жёстких задач, чем метод трапеций по схеме ПК с итерациями Ньютона и регулируемой точностью.

Решение нелинейных уравнений методами Ньютона, секущих и релаксации.

Исходные параметры:

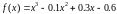
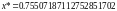- решение уравнения ;

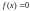- интервал;

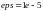- точность;

Расчёты прочих условий:

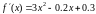
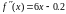
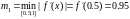
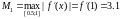
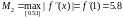
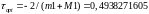
Проверка условий сходимости:

1) Метод Ньютона:

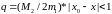- условие квадратичной сходимости. При данных исходных параметрах – выполняется.

Для данной функции метод сходится .

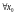2) Метод релаксации:

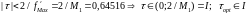
№ итерации	М Е Т О Д
	Релаксации		Секущих			Ньютона
-1	-	-	0.5	-0.35		-	-
0	0.5	-0.35	1	0.6		0.5	-0.35
1	0.67284	-0.13881	0.68421	-0.12124		0.86842	0.24004
2	0.74139	-0.02503	0.73729	-0.03237		0.76794	0.02428
3	0.75375	-0.00244	0.75663	0.00291		0.75526	0.00035
4	0.75496	-0.00020	0.75503	-6.0828е-5		0.75507	7.7565e-8
5	0.75506	-1.6694e-5	0.75507	-1.1056е-7
Трудо- ёмкость	S=7		S=6		S=8

Примечание: пусть i – число потребовавшихся итераций, S – трудоёмкость процесса. Для метода релаксации S=i+2, т.к. до начала итерационного процесса требуется двукратное вычисление значения производной для определения параметра релаксации. Для метода секущих S=i+1, т.к. до начала итерационного процесса вычисляется значение функции в точке 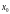. Для метода Ньютона S=2*i, т.к. на каждом шаге вычисляется значение функции и значение производной.