
- •Сравнение естественного и стандартного чисел обусловленности матрицы а также - точного значения стандартного числа обусловленности с его оценкой, вычисленной процедурой decomp:
- •Исследовать возможность улучшения обусловленности задачи посредством внесения малого случайного возмущения в матрицу системы.
- •7 Повторить эксперимент п.6 для 2-3 задач с плохо обусловленной матрицей.
- •8 Выполняя п.П. 6 и 7 , исследовать работоспособность различных методов оценки ошибок решения ( выражения (7), (12), (13) ) при наличии возмущения левой части системы.
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные данные:
- •Исходные данные:
- •Провести исследование влияния вида доминирования матрицы задачи на сходимость процедур Якоби и Гаусса-Зейделя.
- •Исходные данные:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исследовать устойчивость решения задачи среднеквадратичного приближения к погрешности исходных данных.
- •Исходные параметры:
- •Убедиться в справедливости условий чебышевского интерполирования.
- •Исходные параметры:
- •При интегрировании нескольких систем нелинейных уравнений обратить внимание на эффективность различных методов реализации схемы прогноз-коррекция.
- •Исходные параметры:
- •Исходные параметры:
- •При интегрировании жёстких задач:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Дополнительное исследование метода релаксации:
Федеральное государственное бюджетное образовательное учреждение высшего профессионального обучения
САНКТ-ПЕТЕРБУРГКСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Курсовая работа по дисциплине
«Численные методы».
Выполнил студент группы 2092/1:
Трифонов Александр
Преподаватель:
Зудов
Роман Игоревич
Лектор курса:
проф. Синепол
Владислав Степанович
Санкт-Петербург
2012 год
ОГЛАВЛЕНИЕ
ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ЧИСЛЕННЫХ МЕТОДОВ
РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ…………………… 3
ИССЛЕДОВАНИЕ ИНТЕРПОЛИРОВАНИЯ ФУНКЦИЙ………………..………………...…..11
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ…………………….……....….23
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДАМИ НЬЮТОНА,
СЕКУЩИХ И РЕЛАКСАЦИИ……………………………………………………………....….…34
ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ЧИСЛЕННЫХ МЕТОДОВ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Сравнение естественного и стандартного чисел обусловленности матрицы а также - точного значения стандартного числа обусловленности с его оценкой, вычисленной процедурой decomp:
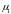 - естественное
число обусловленности:
- естественное
число обусловленности:
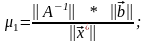
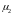 - стандартное
число обусловленности:
- стандартное
число обусловленности:
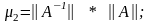
cond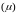 - оценка
стандартного числа обусловленности,
полученная с помощью
процедуры
DECOMP:
- оценка
стандартного числа обусловленности,
полученная с помощью
процедуры
DECOMP:
-
Номер матрицы
Порядок матрицы
cond
2
3
1.760E+01
2.400E+01
1.933E+01
8
2.089E+01
1.440E+02
1.353E+02
11
3
1.736E+01
7.003E+03
5.947E+03
8
4.660E+12
2.496E+14
5.763E+13
Для
хорошо обусловленной матрицы разница
между естественным и стандартным числами
обусловленности мала (в пределах
порядка). Для плохо обусловленной матрицы
естественное и стандартное числа
обусловленности отличаются более
значительно (в эксперименте это отличие
составило два порядка). Это происходит
оттого, что естественное число
обусловленности содержит вектор
машинного решения
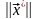 ,
который
для плохо обусловленных матриц может
достаточно много отличаться от точного
вектора решения.
,
который
для плохо обусловленных матриц может
достаточно много отличаться от точного
вектора решения.
Тем не менее, точное и оценочное значение естественного числа отличаются (относительно) мало (максимальное различие, полученное ходе эксперимента – один порядок) для матриц разной обусловленности. Поэтому можно говорить о допустимости использования процедуры DECOMP для оценки стандартного числа обусловленности.
Оценка точности решений, получаемых методом исключения Гаусса для систем с одинаково хорошо обусловленными матрицами порядка от 3 до 15; анализ точности, как функции порядка матрицы; сравнение фактически получаемой ошибки с ее оценками:
-
Номер матрицы
Порядок матрицы
cond
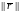
Real Error
ErrEst(cond)
1
3
1.175E+0001
0
0
0
7
3.241E+0002
0
0
0
10
4.953E+0003
0
0
0
12
3.231E+0004
0
0
0
15
5.622E+0005
0
0
0
4
3
6.840E+0000
9.233E-0012
1.039E-0012
4.28E-0012
7
6.986E+0000
3.489E-0010
1.323E-0012
1.01E-0011
10
2.376E+0002
7.750E-0010
9.917E-0012
9.27E-0010
12
2.854E+0001
1.312E-0010
3.946E-0012
5.73E-0011
15
3.618E+0001
2.441E-0010
6.029E-0012
1.40E-0010
Для хорошо обусловленных матриц точность решения высока и приблизительно одинакова для задач разного порядка. С ростом порядка растёт различие между точностью и её оценкой (в эксперименте максимальное различие составило два порядка). Это связано с дополнительным количеством математических операций, проводимых при оценке: их количество увеличивается с ростом порядка матрицы.
3 Оценка точности решений, получаемых методом исключения Гаусса для систем с одинаково плохо обусловленными матрицами порядка от 3 до 15; анализ точности, как функции порядка матрицы; сравнение фактически получаемой ошибки с ее оценками:
-
Номер матрицы
Порядок матрицы
cond
Real Error
ErrEst(cond)
5
3
6.808E+0002
7.579E-0013
2.001E-0011
6.59E-0011
7
7.419E+0008
1.814E-0011
5.026E-0006
3.71E-0004
10
2.262E+0013
7.317E-0013
1.144E-0001
3.16E+0000
12
7.553E+0013
1.329E-0011
1.598E+0000
6.47E+0001
15
5.783E+0013
1.859E-0011
1.166E+0001
1.45E+0002
11
3
5.947E+0003
3.227E-0012
1.353E-0010
2.59E-0008
7
4.647E+0011
8.594E-0011
2.860E-0002
3.16E-0001
10
6.310E+0013
1.783E-0010
1.483E+0000
8.76E+0001
12
7.613E+0013
1.023E-0010
4.008E+0000
1.51E+0002
15
7.173E+0014
6.621E-0010
9.896E+0000
7.40E+0003
Для плохо обусловленных матриц точность значительно падает с увеличением порядка матрицы. Тем не менее, различие между точностью и её оценкой остаётся в пределах трёх порядков, причём значение оценки ошибки больше значения самой ошибки. Таким образом, можно утверждать, что оценка ошибки является приемлемой, о чём также свидетельствуют результаты п.2.
4 Оценка точности решений, получаемых методом исключения Гаусса для систем одного порядка, но различной обусловленности (от «очень хороших» до «очень плохих»).
-
Порядок матрицы
Номер матрицы
cond
Real Error
ErrEst(cond)
3
4
4.683E+0001
1.223E-0011
3.234E-0012
3.94E-0011
6
1.687E+0004
1.091E-0011
5.336E-0011
4.46E-0009
11
5.947E+0003
5.776E-0012
1.528E-0010
5.35E-0009
13
5.939E+0003
5.197E-0013
1.572E-0010
6.27E-0010
7
4
1.466E+0002
1.308E-0011
2.381E-0011
1.47E-0010
6
1.215E+0017
3.237E-0010
1.911E+0001
7.11E+0004
11
4.647E+0011
1.331E-0011
3.475E-0002
3.24E-0001
13
5.758E+0007
5.571E-0012
2.496E-0006
3.22E-0005
С ростом числа обусловленности матрицы растёт ошибка решения, что подтвердилось в данном эксперименте. Норма вектора невязки же с ростом обусловленности остаётся весьма малой, из чего заключаем, что вектор невязки не годен в качестве критерия точности решения задачи.
