
- •Сравнение естественного и стандартного чисел обусловленности матрицы а также - точного значения стандартного числа обусловленности с его оценкой, вычисленной процедурой decomp:
- •Исследовать возможность улучшения обусловленности задачи посредством внесения малого случайного возмущения в матрицу системы.
- •7 Повторить эксперимент п.6 для 2-3 задач с плохо обусловленной матрицей.
- •8 Выполняя п.П. 6 и 7 , исследовать работоспособность различных методов оценки ошибок решения ( выражения (7), (12), (13) ) при наличии возмущения левой части системы.
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные данные:
- •Исходные данные:
- •Провести исследование влияния вида доминирования матрицы задачи на сходимость процедур Якоби и Гаусса-Зейделя.
- •Исходные данные:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исследовать устойчивость решения задачи среднеквадратичного приближения к погрешности исходных данных.
- •Исходные параметры:
- •Убедиться в справедливости условий чебышевского интерполирования.
- •Исходные параметры:
- •При интегрировании нескольких систем нелинейных уравнений обратить внимание на эффективность различных методов реализации схемы прогноз-коррекция.
- •Исходные параметры:
- •Исходные параметры:
- •При интегрировании жёстких задач:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Исходные параметры:
- •Дополнительное исследование метода релаксации:
Исходные параметры:
Интервал:
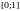
-
№ задачи
Шаг
Ошибка численного решения
Явн. Эйлера
Неявн. Эйлера
РК2
РК3
РК4
2
1e-1
3е-1
1е-1
8е-2
2е-2
3е-3
1e-2
1е-2
1е-2
4е-4
9е-6
2е-7
13
1e-1
2е-1
2е-1
7е-3
2е-4
3е-6
1e-2
3е-3
3е-3
1е-4
2е-7
5е-10
Погрешности
методов Эйлера ведут себя как
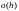 ,
погрешности методов Рунге-Кутты - как
,
погрешности методов Рунге-Кутты - как
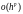 (
(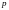 -
порядок метода). Поэтому методы Рунге-Кутты
показали большую, чем методы Эйлера,
точность. Также, можно заключить, что
при неизменном порядке метода с
уменьшением шага (при
-
порядок метода). Поэтому методы Рунге-Кутты
показали большую, чем методы Эйлера,
точность. Также, можно заключить, что
при неизменном порядке метода с
уменьшением шага (при
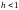 )
увеличивается точность решения; а при
неизменном шаге (снова при
)
большую точность показывает метод
большего порядка.
)
увеличивается точность решения; а при
неизменном шаге (снова при
)
большую точность показывает метод
большего порядка.
Качественное поведение погрешности решений для методов не отличается – различие лишь в гладкости (в зависимости от шага) и величине ошибки (в зависимости от порядка метода) –
об этом свидетельствуют приложения 2а и 2б.
Полученные
результаты можно объяснить схожестью
вычислительных схем:
методы явные и неявные Рунге-Кутты
фактически представляют собой
«модернизацию» явных и неявных методов
Эйлера (в эксперименте исследовались
лишь явные методы Рунге-Кутты).
Действительно, явную схему Эйлера можно
представить как
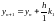 ,
где
,
где
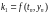 ;
аналогичное
можно утверждать и для неявного метода
Эйлера, заменив
;
аналогичное
можно утверждать и для неявного метода
Эйлера, заменив
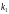 на
на
 .
Таким
образом, методы Эйлера можно условно
назвать методами Рунге-Кутты первого
порядка, чем и объясняются полученные
результаты.
.
Таким
образом, методы Эйлера можно условно
назвать методами Рунге-Кутты первого
порядка, чем и объясняются полученные
результаты.
При интегрировании жёстких задач:
а) получить экспериментальные характеристики эффективности явных методов (РК4, явный Эйлера);
б) установить возможность и условия интегрирования задачи неявными методами с (метод трапеции);
в) сравнить эффективность применения метода Гира второго порядка и метода трапеции
а) Исследование эффективности явных методов.
Исходные параметры:
Задача №4 (линейная)
Интервал:

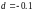 ;
;
-
Eps
Шаг
Ошибка численного решения
Явн. Эйлера
РК4
1е-4
3e-4
Останов*
Останов
2e-4
1е+0
1е-1
1e-5
8e-3
1e-7
1е-6
8е-4
4е-11
1е-5
3e-5
Останов
Останов
2e-5
1е+0
3е-8
1е-5
3е-9
8е-12
1е-6
3е-10
3е-11
* - Неустойчивость вычислительной схемы.
