1.2.2. Фильтры Баттерворта

При решении задач обработки навигационной информации нередко приходится иметь дело с так называемыми фильтрами Баттерворта, которые и рассмотрим в настоящем подразделе. Введем полином порядка [41, с. 178]

, (1.2.13)

где . Корни этого полинома находятся по формуле

, (1.2.14)

и равномерно размещаются на окружности радиуса в вершинах правильного -угольника. Под фильтром Баттерворта будем понимать систему с ПФ

, (1.2.15)

у которой полюса характеристического полинома совпадают с теми корнями , у которых . Полином

, (1.2.16)

с таким образом введенными корнями называется полиномом Баттерворта, а при нормированным полиномом Баттерворта [41, с. 178 ].

Если ввести и корни для нормированного полинома Баттерворта, то ПФ (1.2.15) может быть записана как

.

ЧХ для фильтров Баттерворта определяtтся в виде

.

Для амплитудно-частотной характеристики справедливо следующее представление [65, с.128]

,

где . Частота называется частотой среза фильтра Баттерворта.

В табл. 1.2.1 представлены корни и ПФ для нормированных фильтров Баттерворта первого, второго и третьего порядков [41].

Т а б л и ц а 1.2.1

Корни и ПФ нормированных фильтров Баттерворта

	Корни	Передаточная функция
1
2	,
3

В пространстве состояний система, описывающая фильтр Баттерворта -го порядка, может быть представлена с помощью уравнений (1.1.14), (1.1.15), в которых

, (1.2.17)

, . (1.2.18)

При этом коэффициенты , совпадают с коэффициентами полинома Баттерворта. К примеру, формирующий фильтр для нормированного фильтра Баттерворта второго порядка можно получить, если в матрице (1.2.17) при n = 2 , , тогда:

,

;

.

На рис. 1.2.1 изображены графики амплитудно-частотной характеристики для нормированных фильтров Баттерворта при n = 1, 2,3. Из этих графиков следует, что при увеличении порядка фильтра Баттерворта эта характеристика приближается к прямоугольной. Именно это свойство и определило широкое применение фильтров Баттерворта в задачах обработки информации.

Рис. 1.2.1. Амплитудно-частотные характеристики фильтров Баттерворта

1.2.3. Модель акселерометра

Приближенное линеаризованное уравнение для осевого акселерометра (рис. 1.2.2) без учета влияния возмущений можно записать в виде [59, с. 31; 61, с. 87]

(1.2.19)

или ,

где – инерционная масса чувствительного элемента (ЧЭ); – абсолютный коэффициент демпфирования; – коэффициент жесткости пружины (отношение прилагаемой силы к изменению длины ) в направлении .

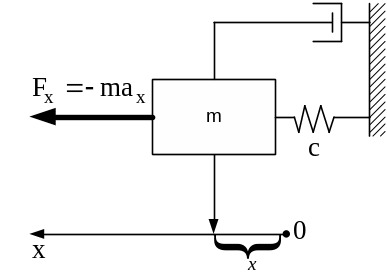
Рис. 1.2.2. Схема осевого акселерометра

Вводя обозначения , , запишем

. (1.2.20)

Величина называется собственной частотой колебаний инерционной массы, а – относительным коэффициентом демпфирования или показателем затухания. Это уравнение при описывает систему (звено), которая в теории автоматического управления известно как колебательное звено [7, с. 74].

Нетрудно убедиться в том, что ПФ, ЧХ, амплитудно-частотная и фазочастотная характеристики, соответствующие (1.2.20), имеют следующий вид [61]:

; (1.2.21)

; (1.2.22)

; (1.2.23)

. (1.2.24)

где – постоянная времени акселерометра;  передаточный коэффициент.

Примеры амплитудно-частотных и фазочастотных характеристик (1.2.22), (1.2.23) приведены на рис. 1.2.3.

Используя результаты подраздела 1.6, легко показать, что для описания поведения акселерометра в пространстве состояний можно использовать модель:

(1.2.25)

. (1.2.26)

При , как следует из п. 3 примера П6, приведенного в подразделе П2.3, характеристическое уравнение имеет два комплексно-сопряженных корня , где , а , что соответствует устойчивой системе. Фундаментальная матрица для этой системы задается соотношением (П2.36). Поскольку в данном случае , , то согласно (1.1.16) весовая функция будет определяться как .

а)

б)

Рис. 1.2.3. Пример амплитудно-частотной (1.2.23) (а) и фазочастотной (1.2.24) (б) характеристик при , ,

Приведенные модели могут быть использованы для исследования свойств акселерометра [61, с. 86]. В частности, предположим, что на входе акселерометра действует постоянное ускорение . Тогда в операторной форме выходной сигнал, определяющий реакцию акселерометра на постоянный сигнал при нулевых начальных условиях, будет задаваться соотношением

.

Нетрудно убедиться (см. задачу 1.2.2), что, поскольку , функция времени, соответствующая второму слагаемому, при увеличении времени стремится к нулю. Таким образом, при постоянном ускорении ЧЭ акселерометра имеет постоянное смещение

.

Определим ошибку акселерометра как

и предположим, что помимо полезного сигнала на акселерометр воздействует внешнее возмущающее ускорения . Вводя преобразования Фурье , , , для , , и и используя ЧХ, можем записать:

.

Ясно, что для воспроизведения полезного сигнала с малой ошибкой необходимо, чтобы, с одной стороны, , а с другой – для подавления возмущающих ускорений желательно, чтобы . Понятно, что обеспечение столь противоречивых требований возможно лишь в случае, когда частотный состав полезного сигнала существенно отличается от частотного состава возмущений. Располагая информацией о частотном составе полезного сигнала и возмущений, можно, изменяя конструктивные параметры акселерометра или добавляя на выходе устройство обработки (фильтр), постараться обеспечить соответствующие свойства ЧХ. Именно такая задача и решается далее в подразделе 3.1 при построении оптимальных фильтров.